前言：本文内容主要包括2部分：

1. MSE简介、sklearn案例（案例：线性回归、随机森林_加利福尼亚房价数据集）

2. 简介、sklearn案例、为负时公式推导 （案例：交叉验证_加利福尼亚房价数据集）

如何查看均方误差判断预测结果是否正确？

为什么要使用均方误差，之前的准确率不行吗？

因为回归类模型结果是连续型变量，无法直接使用正确或错误来判断。但可以用预测值与真实值之间的差异来判断模型的优劣，差异越小，说明模型越好。 

这种衡量差异的公式可以写为： 

其中m表示特征数量，i表示样本数量，表示预测值；这个公式称为均方误差，在sklearn的metrics模块中为mean_squared_error；cross_val_score为scoring中的neg_mean_squared_error，以负数表示。 

---

案例：线性回归模型MSE评估_加利福尼亚房价数据集

from sklearn.metrics import mean_squared_error
mse_metrics=mean_squared_error(y_hat,y_test) # 返回均方误差,越小越好
print(mse_metrics)
# 0.5511198138984461
mse_metrics/(y_test.mean()) 
# 0.26678247569102054

from sklearn.model_selection import cross_val_score
mse_cvs=cross_val_score(model,X_test,y_test
                        ,cv=10
                        ,scoring='neg_mean_squared_error'
                       ).mean()  
# 返回均方误差，由于X_test有异常值，导致交叉验证中如果抽中该数据，则均方误差特别大
print(mse_cvs)
# -4.583931708384997
mse_cvs/(y_test.mean())
# -2.2189596866623678

# 对比随机森林，均方误差的结果更加稳定
from sklearn.ensemble import RandomForestRegressor
model_rf=RandomForestRegressor().fit(X_train,y_train)
y_hat_rf=model_rf.predict(X_test)
print(mean_squared_error(y_hat_rf,y_test))
# 0.24656335621845812

print(cross_val_score(model_rf,X_test,y_test
                      ,cv=10
                      ,scoring='neg_mean_squared_error'
                     ).mean())
# -0.3152072055910439  # 显示为负，其实是正数

---

补充：

还可以使用MAE（绝对均值误差）来表示，公式为：

 metrics中为mean_absolute_error；cross_val_score中为neg_mean_absolute_error。

---

如何评估数据的分布情况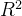？与MSE的区别？ 

均方误差MSE的公式为： 

由公式可知，MSE衡量的是真实值与预测值差异的平方和，除以m。 

由于需要除以m，所以可能会一定程度掩盖真实值与预测值的差异。比如一部分真实值和预测值完全吻合；而另一部分真实值和预测值差异非常大，经过平均之后，差异很大的部分就不会被MSE反映出来。 

这是因为MSE虽然可以反映数据的差异，但是不能反映数据的分布。

解决这个问题的指标为R^2，其公式为： 

其中残差平方和：，为均值；可以理解为，1-模型没有捕捉到的信息/模型携带的信息；模型没有捕捉到的信息越低越好，所以越接近1，模型效果越好。 

---

在sklearn中的应用案例如下（案例：线性回归模型评估_加利福尼亚房价数据集） ：

# R^2在sklearn中的应用
from sklearn.metrics import r2_score
r2_score(y_true=y_test,y_pred=y_hat)
# 0.5874855472168157

from sklearn.model_selection import cross_val_score
cross_val_score(model,X_test,y_test,cv=5,scoring='r2')
# -1.9878822659956534 
# array([-12.34077988,   0.60497249,   0.60384174,   0.5977602 ,
         0.59479412])
    
# 同样由于X_test有异常值，所以出现了-12的r^2

---

 从上面的案例中发现，会出现负数，这种情况应该怎么理解呢？

回到的公式，也称为总离差平方和（TSS），所以的公式为： 

其中TSS的公式可以进行如下推导： 

（中间左边变成1的那一步，是因为左右同时除以TSS）

因为ESS和TSS为正数，所以当为负时，为负。会出现这种情况，可能是预测值和真实值差异过大导致的。

当模型拟合效果极差时，会出现为负的情况，这时应该考虑更换模型。