一、问题

1、测试集性能与真正的泛化性能未必一致

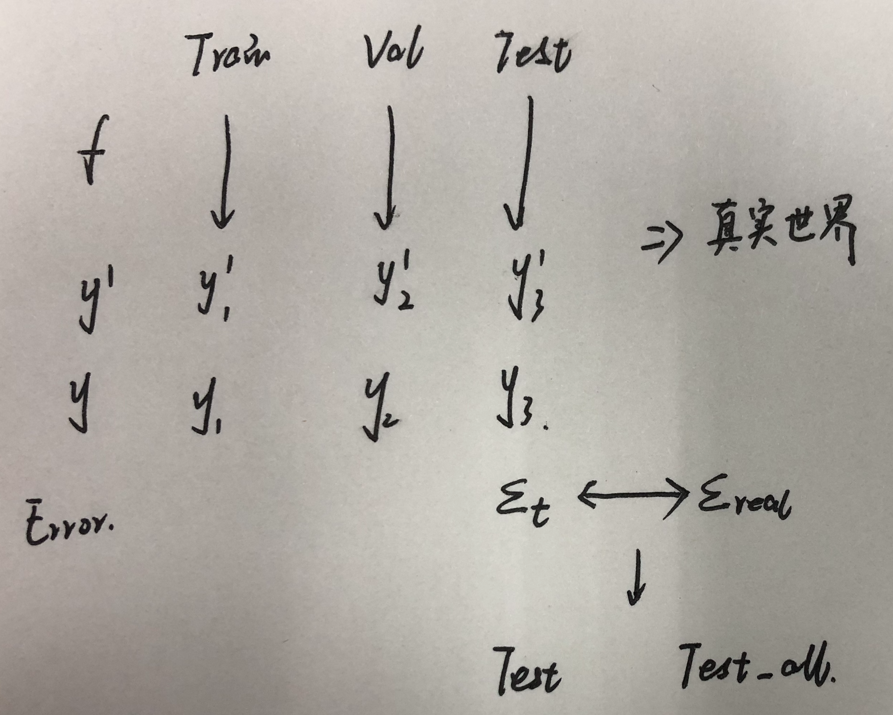
2、测试集不同反映的性能不同：多个测试集结果不同

3、机器学习算法本身有一定的随机性，同一个测试集上多次运行，可能会有不同的结果。

二、数学基础

B站：小元老师高数线代概率

三、一个测试集一种算法

（1）二项分布：

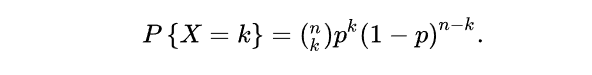
假设真实世界错误率为，则测试集中错误率的概念分布应该为二项分布

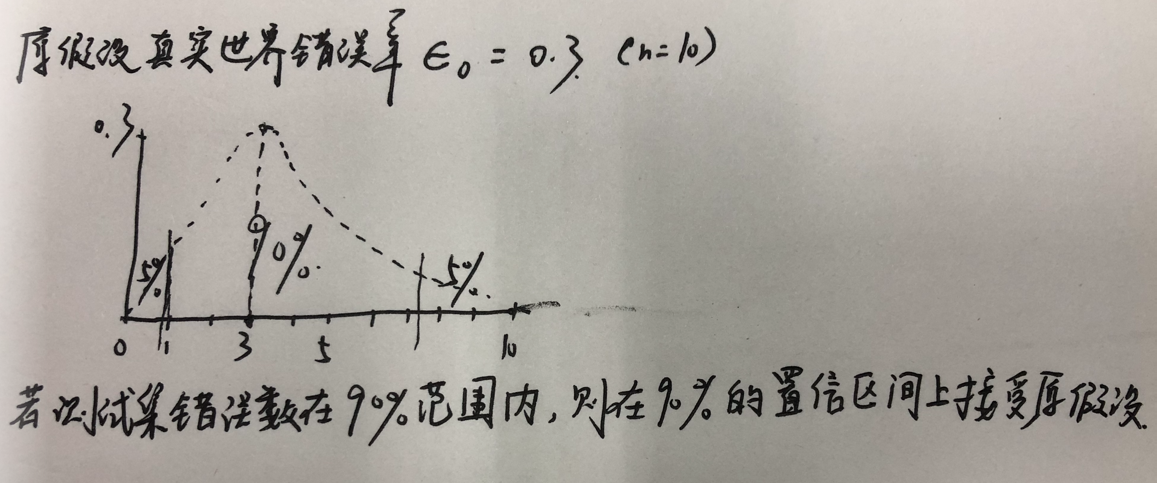
 大致分布如图，其中峰顶对应横轴应为np，纵轴为错误率0.3。其中n为总样本数量。 

 （2）假设检验

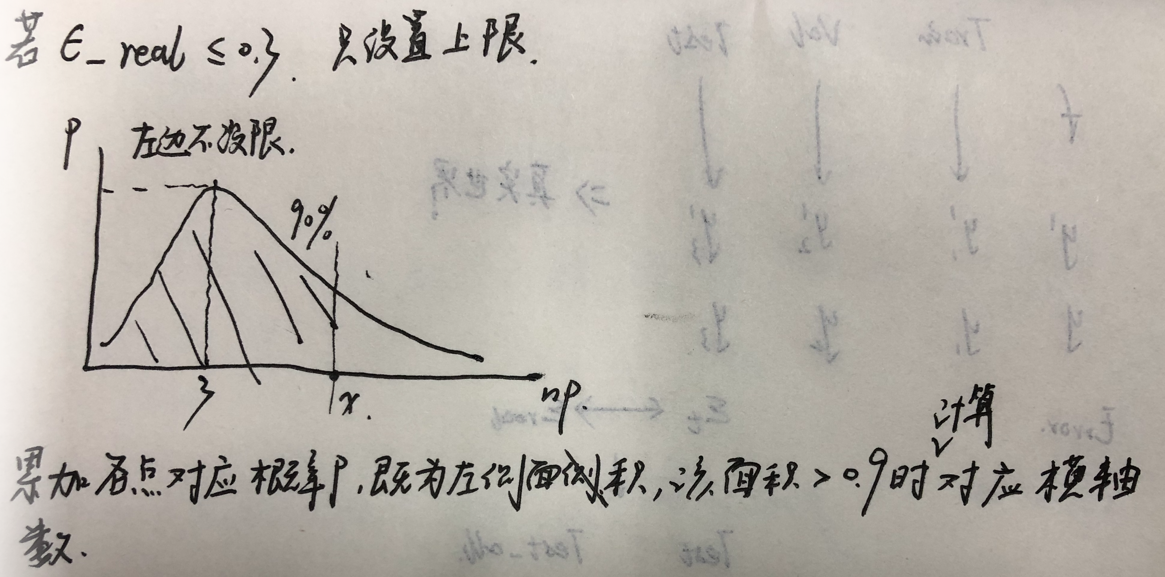
1）置信区间：

四、多个测试集一种算法——t检验

1、根据多个测试集错误率，计算得样本（错误率）均值以及样本方差

2、又已知

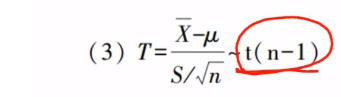
详细推导见三大分布及正态总体下的抽样分布（待完善）_Checkmate9949的博客-CSDN博客三大分布及正态总体下的抽样分布（待完善）_Checkmate9949的博客-CSDN博客

 3、以对应样本均值，真实错误率对应真实均值，则

 

 

 与“一个测试集一种算法”同理，通过自由度(k-1)以及置信度alpha即可得出对应的临界值。超出临界值则拒绝原假设。

五、多个测试集两种算法——交叉验证t检验：验证两种算法是否存在显著差别

1、K折交叉验证：CSDN

2、变量及临界值

 3、样本独立性

（1）测试集错误率相当于抽样样本，泛化错误率相当于总体。在K折交叉中，其训练集是重叠的，这就导致测试集错误率不独立，及抽样样本不独立，那么t分布也就不成立了。

（2）为解决上述问题。可应用5*2交叉验证法。

即做5次2折交叉验证。

六、一种测试集两种算法——McNemar检验

 

 这里分子减一的目的：考虑连续性矫正。

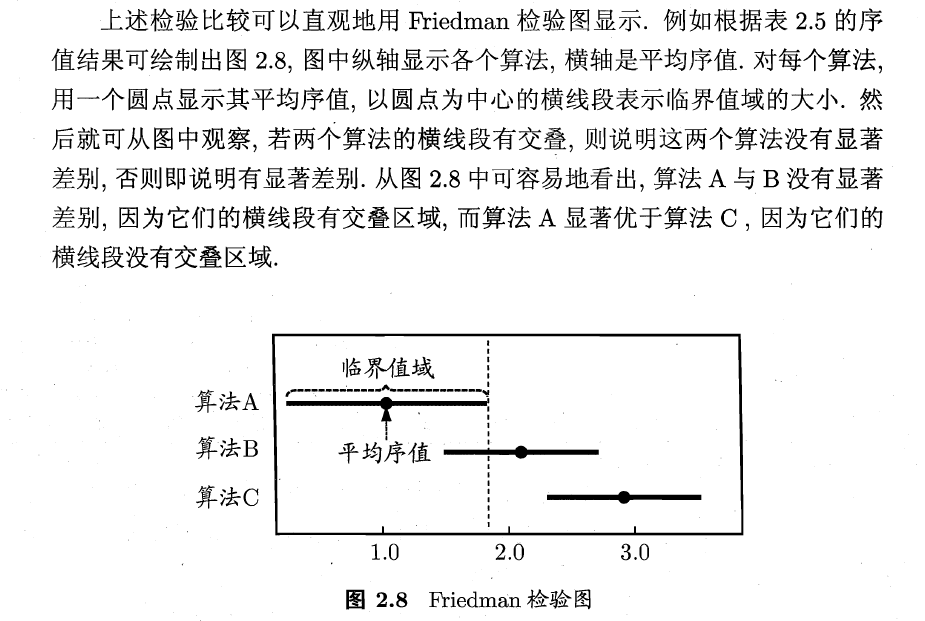
七、多个测试集多种算法——Friedman检验与Nemenyi后验检验

1、多个测试集多种算法的比较思路

（1）每个数据集分别列出两两比较的结果；

（2）基于算法排序的Friedman检验。

2、Friedman检验的思路：

（1）通过留出法或交叉验证法得到每个算法在每个数据集的测试结果：

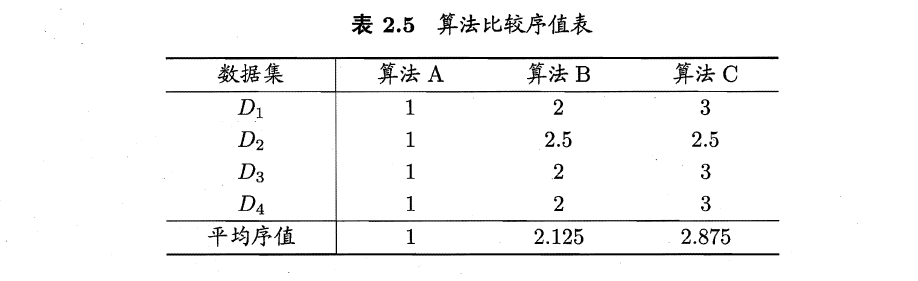
 （2）原始Friedman检验

 根据卡方分布性质便可确定临界值。

（3）Friedman检验

 

 （4）Nemenyi后续检验

 （5）例子

 

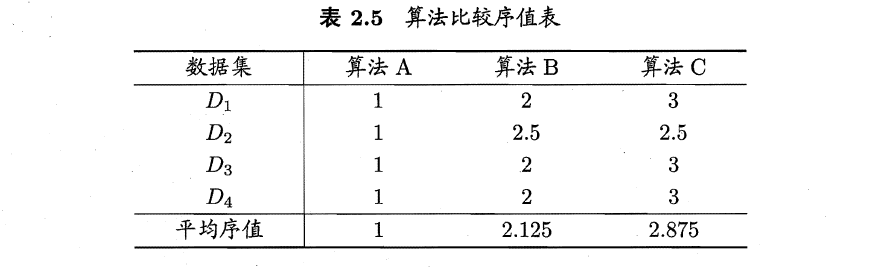
 1）根据式

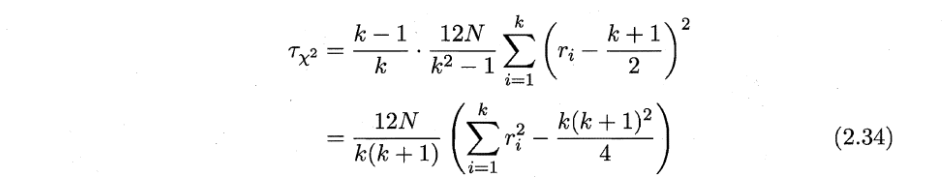
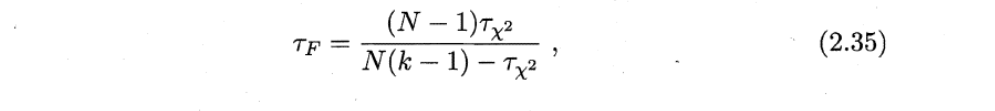
 计算得

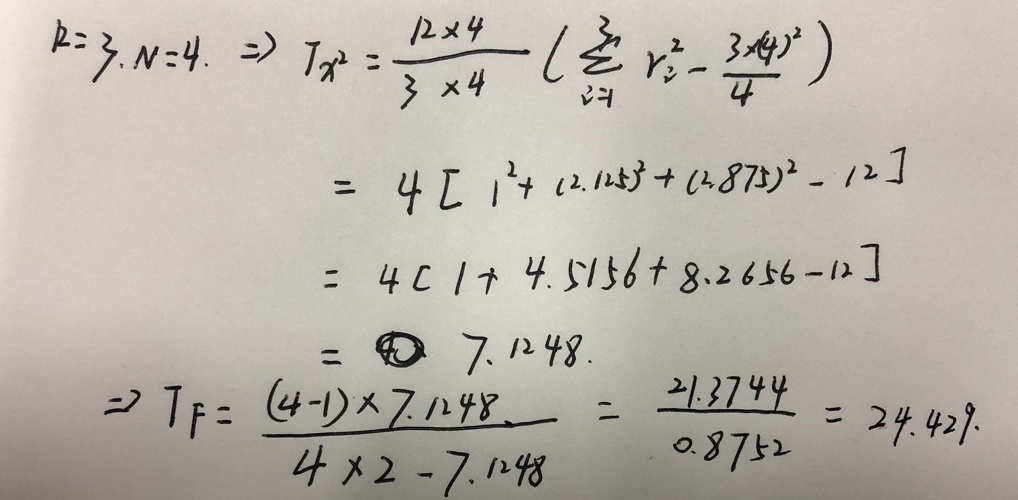
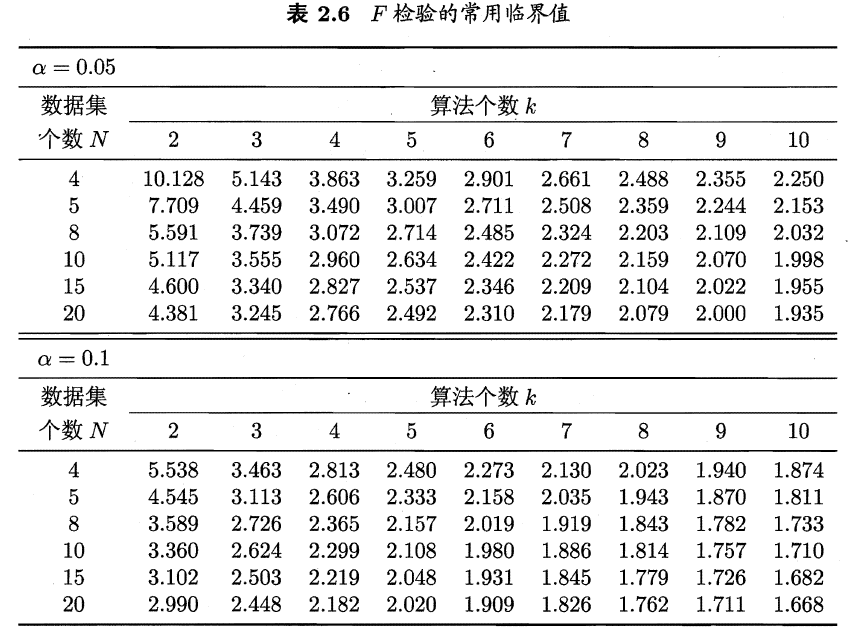
 2）与k=3对应得临界值对比，发现其远远大于临界值，拒绝算法性能相同的原假设。

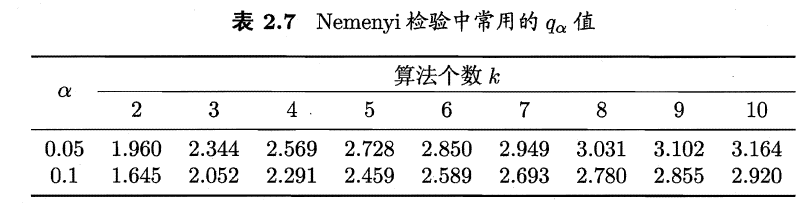
 3）Nemenyi后续检验