链接：Maxwell-Jia/AIME_2024 · Datasets at Hugging Face

数据集描述​​
该数据集包含来自 2024 年美国数学邀请赛 (American Invitational Mathematics Examination, AIME) 的题目。AIME 是一项以其极具挑战性的数学问题而闻名的、享有盛誉的高中数学竞赛。

​​数据集详情​​

• ​​格式：​​ JSONL
• ​​大小：​​ 30 条记录
• ​​来源：​​ AIME 2024 I & II (2024 年 AIME 邀请赛 I 轮 和 II 轮)
• ​​语言：​​ 英语

​​数据字段​​
每条记录包含以下字段：

• ​​ID：​​ 问题标识符（例如，“2024-I-1”代表 2024 年 I 轮竞赛的第 1 题）
• ​​Problem：​​ 题目陈述
• ​​Solution：​​ 详细的解答过程
• ​​Answer：​​ 最终的数字答案

​​用途​​
该数据集主要用于：

• 评估大型语言模型 (Large Language Models, LLMs) 的数学推理能力
• 测试模型在复杂数学问题上的解决能力
• 研究人工智能在结构化数学任务上的表现

​​特点​​

• 涵盖多种数学领域（几何、代数、数论等）
• 包含每道题的详细解答过程
• 所有题目都有具体的数字答案
• 难度高，适合测试高级推理能力
• 问题需要多步推理和数学洞察力

使用与查看

题目和答案都在最后一个文件aime_2024_problems.parquet里面，下载之后使用以下代码读取，打印，显示：

import pandas as pd
import pyarrow.parquet as pq

# 读取整个文件
df = pd.read_parquet('aime_2024_problems.parquet')

# 读取Parquet文件的元数据
table = pq.read_table('aime_2024_problems.parquet', use_threads=True)
schema = table.schema

# 获取所有字段名
field_names = schema.names

# 获取有多少个用例
parquet_file = pq.ParquetFile('aime_2024_problems.parquet')
num_rows = parquet_file.metadata.num_rows
print(f"文件总行数: {num_rows}")

# 获取字段详细信息（名称和数据类型）
print("字段详细信息：")
for field in schema:
    print(f"- {field.name}: {field.type}")
print("--------------------")

specific_rows = df.iloc[0] 
print("ID:", specific_rows['ID'])
print("Problem:", specific_rows['Problem'])
print("Solution:", specific_rows['Solution'])
print("Answer:", specific_rows['Answer'])

结果：

文件总行数: 30
字段详细信息：
- ID: string
- Problem: string
- Solution: string
- Answer: int64
--------------------
ID: 2024-II-4
Problem: Let $x,y$ and $z$ be positive real numbers that satisfy the following system of equations:
\[\log_2\left({x \over yz}\right) = {1 \over 2}\]
\[\log_2\left({y \over xz}\right) = {1 \over 3}\]
\[\log_2\left({z \over xy}\right) = {1 \over 4}\]
Then the value of $\left|\log_2(x^4y^3z^2)\right|$ is $\tfrac{m}{n}$ where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
Solution: Denote $\log_2(x) = a$, $\log_2(y) = b$, and $\log_2(z) = c$.

Then, we have:
$a-b-c = \frac{1}{2}$,
$-a+b-c = \frac{1}{3}$,
$-a-b+c = \frac{1}{4}$.

Now, we can solve to get $a = \frac{-7}{24}, b = \frac{-9}{24}, c = \frac{-5}{12}$.
Plugging these values in, we obtain $|4a + 3b + 2c|  = \frac{25}{8} \implies \boxed{033}$.
Answer: 33

评价指标

ACC（准确率） 是最基础的评估指标，计算公式为：

ACC=模型正确回答的问题数/评测集总问题数

即模型输出结果与标准答案完全匹配的问题占比。

AIME24 要求答案必须为 0~999 的整数（符合原竞赛规则）。ACC 仅当模型输出完全等于标准答案的整数时计为正确。

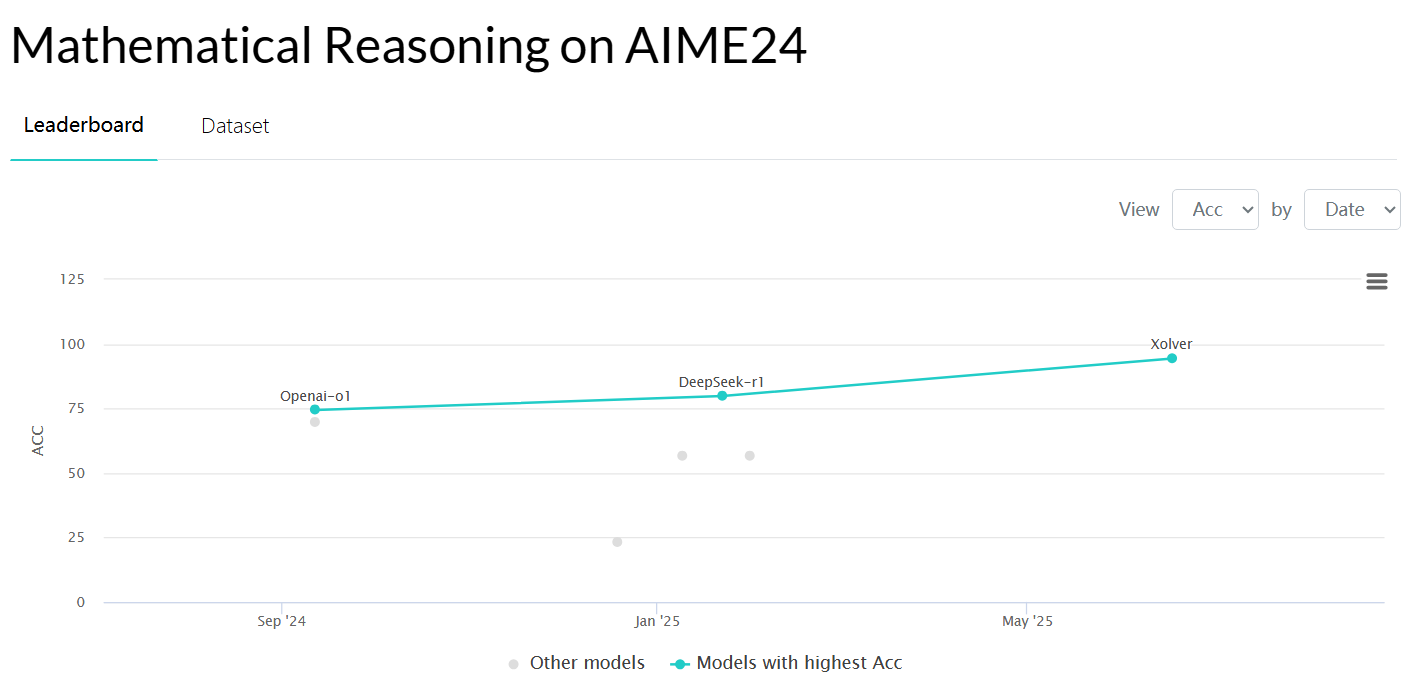
AIME24 Benchmark (Mathematical Reasoning) | Papers With Code