一、引言

DFS 和 BFS 分别依赖栈和队列的特性，它们是图算法中核心的遍历方法，并广泛应用于路径搜索等问题。

二、图的基础概念

图（Graph）是由顶点（Vertex）和边（Edge）组成的数据结构：

• 顶点（Vertex）：表示图中的对象或节点。

• 边（Edge）：表示顶点之间的关系。

图的分类

1.无向图：边无方向性，表示顶点之间是对等的关系。例如：好友关系。
2.有向图：边具有方向性，表示顶点之间的关系是单向的。例如：关注关系。
3.带权图：边具有权值，用于表示两个顶点之间的关系具有不同的“重”。例如：距离、费用。

图的表示方式

1.邻接矩阵（Adjacency Matrix）

通过二维数组存储顶点间的连接关系。适合用于边比较多的图。

邻接矩阵示例：如下无向图。

A -- B  
|    |  
C -- D  

邻接矩阵表示

用二维数组matrix表示图的连接关系，其中：

matrix[i][j] = 1表示顶点i和顶点j之间有边。

matrix[i][j] = 0表示顶点i和顶点j之间没有边。

顶点编号：

A → 0

B → 1

C → 2

D → 3

邻接矩阵：

    A(0) B(1) C(2) D(3)
A(0)  0    1    1    0
B(1)  1    0    0    1
C(2)  1    0    0    1
D(3)  0    1    1    0

代码实现：

public class AdjacencyMatrixExample {
    public static void main(String[] args) {
        // 定义图的顶点数
        int vertices = 4;

        // 初始化邻接矩阵
        int[][] matrix = new int[vertices][vertices];

        // 添加边（无向图）
        addEdge(matrix, 0, 1); // A -- B
        addEdge(matrix, 0, 2); // A -- C
        addEdge(matrix, 1, 3); // B -- D
        addEdge(matrix, 2, 3); // C -- D

        // 打印邻接矩阵
        System.out.println("邻接矩阵：");
        printMatrix(matrix);
    }

    // 添加边的辅助方法
    private static void addEdge(int[][] matrix, int i, int j) {
        matrix[i][j] = 1; // 无向图需要对称
        matrix[j][i] = 1;
    }

    // 打印邻接矩阵
    private static void printMatrix(int[][] matrix) {
        for (int[] row : matrix) {
            for (int value : row) {
                System.out.print(value + " ");
            }
            System.out.println();
        }
    }
}

输出：
邻接矩阵：

0 1 1 0 
1 0 0 1 
1 0 0 1 
0 1 1 0 

2.邻接表（Adjacency List）

使用列表存储每个顶点的邻接顶点集合，节省空间，适用于稀疏图。

邻接表示例：还是如下无向图。

A -- B  
|    |  
C -- D  

顶点编号：

A → 0

B → 1

C → 2

D → 3

邻接表：

A(0) -> [B(1), C(2)]
B(1) -> [A(0), D(3)]
C(2) -> [A(0), D(3)]
D(3) -> [B(1), C(2)]

代码实现：

import java.util.*;

public class AdjacencyListExample {
    public static void main(String[] args) {
        // 定义图的顶点数
        int vertices = 4;

        // 初始化邻接表
        List<List<Integer>> adjList = new ArrayList<>();
        for (int i = 0; i < vertices; i++) {
            adjList.add(new ArrayList<>());
        }

        // 添加边（无向图）
        addEdge(adjList, 0, 1); // A -- B
        addEdge(adjList, 0, 2); // A -- C
        addEdge(adjList, 1, 3); // B -- D
        addEdge(adjList, 2, 3); // C -- D

        // 打印邻接表
        System.out.println("邻接表：");
        printAdjList(adjList);
    }

    // 添加边的辅助方法
    private static void addEdge(List<List<Integer>> adjList, int i, int j) {
        adjList.get(i).add(j); // 无向图需要双向添加
        adjList.get(j).add(i);
    }

    // 打印邻接表
    private static void printAdjList(List<List<Integer>> adjList) {
        for (int i = 0; i < adjList.size(); i++) {
            System.out.print("顶点 " + i + " -> ");
            for (int neighbor : adjList.get(i)) {
                System.out.print(neighbor + " ");
            }
            System.out.println();
        }
    }
}

输出：

邻接表：

顶点 0 -> 1 2 
顶点 1 -> 0 3 
顶点 2 -> 0 3 
顶点 3 -> 1 2 

三、深度优先搜索（DFS）

1. 原理解析
深度优先搜索（DFS）是一种递归算法，遍历图时先访问一个节点，并递归访问其所有未访问的邻居，直到所有路径都遍历完为止。

特点：
深度优先：沿着一条路径探索到底，直到无法继续。
回溯：遇到死胡同时回溯到上一节点。
非唯一性：遍历结果取决于节点的选择顺序。

核心思想：
尽可能深地探索一个分支，直到无法继续时才回溯。

数据结构：
使用栈（手动实现或递归调用栈）来管理节点访问顺序。

实现方式：
递归实现：递归实现依赖于系统调用栈，它通过函数的调用和返回来模拟栈的操作。
显式栈实现：通过ArrayDeque或Stack手动管理回溯过程。在非递归实现中，显式栈管理可以帮助我们手动控制节点的压栈与弹栈过程。

2. DFS 的伪代码

DFS(vertex):
    标记 vertex 为已访问
    遍历 vertex 的所有邻接节点：
        如果该节点未被访问：
            对该节点递归调用 DFS

伪代码描述了深度优先搜索（DFS）的基本步骤，具体包括以下内容：
• 标记节点为已访问
• 遍历邻接节点
• 递归调用 DFS

接下来是具体的 Java 代码实现：

3. 递归实现

import java.util.ArrayList;
import java.util.List;

public class DFSRecursiveExample {

    // 图的邻接表表示，存储每个节点的邻接节点列表
    private static List<List<Integer>> graph = new ArrayList<>();

    // 访问标记数组，记录每个节点是否已访问
    private static boolean[] visited;

    public static void main(String[] args) {
        // 初始化图：假设有 5 个节点，节点编号从 0 到 4
        int nodes = 5;
        visited = new boolean[nodes];  // 初始化访问数组，默认值为 false

        // 初始化图的邻接表
        for (int i = 0; i < nodes; i++) {
            graph.add(new ArrayList<>());
        }

        // 添加边（无向图）
        addEdge(0, 1);  // 节点 0 和 1 之间有边
        addEdge(0, 2);  // 节点 0 和 2 之间有边
        addEdge(1, 3);  // 节点 1 和 3 之间有边
        addEdge(1, 4);  // 节点 1 和 4 之间有边

        // 从节点 0 开始执行 DFS（深度优先搜索）
        System.out.println("DFS (Recursive):");
        dfs(0);  // 调用 DFS，从节点 0 开始
    }

    // 添加图的边（无向图），每条边是双向的
    private static void addEdge(int from, int to) {
        graph.get(from).add(to);  // 从节点 'from' 到 'to' 的边
        graph.get(to).add(from);  // 从节点 'to' 到 'from' 的边（无向图）
    }

    // 递归实现 DFS（深度优先搜索）
    private static void dfs(int node) {
        // 标记当前节点为已访问
        visited[node] = true;

        // 输出当前节点，表示当前正在访问的节点
        System.out.print(node + " ");

        // 遍历当前节点的所有邻接节点
        for (int neighbor : graph.get(node)) {
            // 如果邻接节点未被访问，递归调用 DFS 访问该邻接节点
            if (!visited[neighbor]) {
                dfs(neighbor);  // 递归调用 DFS 访问邻接节点
            }
        }
    }
}

输出：

DFS Recursive: 0 1 3 2

4. 使用栈实现

import java.util.*;

public class DFSStackExample {

    private static List<List<Integer>> graph = new ArrayList<>();
    private static boolean[] visited;

    public static void main(String[] args) {
        // 初始化图：5 个节点，节点编号 0 ~ 4
        int nodes = 5;
        visited = new boolean[nodes]; // 创建一个 visited 数组来标记每个节点是否访问过

        // 初始化邻接表，创建每个节点的邻接列表
        for (int i = 0; i < nodes; i++) {
            graph.add(new ArrayList<>());
        }

        // 添加无向图的边（相互连接的节点）
        addEdge(0, 1);
        addEdge(0, 2);
        addEdge(1, 3);
        addEdge(1, 4);

        // 从节点 0 开始执行 DFS
        System.out.println("DFS (Using Stack):");
        dfs(0);  // 从节点 0 开始深度优先搜索
    }

    // 添加图的边（无向图）
    private static void addEdge(int from, int to) {
        graph.get(from).add(to);  // 在邻接表中添加从 'from' 到 'to' 的边
        graph.get(to).add(from);  // 无向图：同时添加从 'to' 到 'from' 的边
    }

    // 使用栈实现 DFS
    private static void dfs(int start) {
        // 使用栈来模拟递归过程
        Stack<Integer> stack = new Stack<>();
        stack.push(start);  // 将起始节点入栈

        // 当栈不为空时，继续遍历图
        while (!stack.isEmpty()) {
            int node = stack.pop();  // 弹出栈顶元素（即当前要访问的节点）

            // 如果该节点未被访问，标记为已访问并处理（打印）
            if (!visited[node]) {
                visited[node] = true;
                System.out.print(node + " ");  // 输出当前访问的节点
            }

            // 将所有未被访问的邻居节点压入栈
            for (int neighbor : graph.get(node)) {
                if (!visited[neighbor]) {  // 仅当邻居节点未访问过时才压入栈
                    stack.push(neighbor);
                }
            }
        }
    }
}

输出：

DFS (Using Stack):
0 2 1 4 3

四、广度优先搜索（BFS）

1. 原理解析
广度优先搜索（BFS）是一种逐层遍历的算法，从起始节点开始，依次访问当前层的所有邻居节点，再逐层扩展。

特点：
层次遍历：按层级逐步扩展。
最短路径：适合用于寻找无权图的最短路径。

核心思想
遵循“广度优先”，先访问当前节点的所有邻居，再依次深入下一层。

数据结构
使用队列实现节点的访问顺序管理。

实现方式
使用Queue接口（如LinkedList或ArrayDeque）管理节点的访问顺序，确保节点按照其加入队列的顺序被访问。

2. BFS 的伪代码

BFS(start):
    初始化队列，将起始节点加入队列
    标记起始节点为已访问
    当队列非空：
        取出队首节点，输出其值
        遍历其所有邻接节点：
            如果该节点未被访问，将其标记为已访问并加入队列

3. 队列实现

import java.util.*;

public class BFSExample {

    // 定义一个图，使用邻接表来表示
    private static List<List<Integer>> graph = new ArrayList<>();

    // 标记每个节点是否被访问过
    private static boolean[] visited;

    public static void main(String[] args) {
        // 初始化图，假设有 5 个节点，编号为 0 到 4
        int nodes = 5;
        visited = new boolean[nodes];  // 用于记录节点是否已被访问

        // 初始化图的邻接表（每个节点对应一个列表，用于存储与该节点相邻的节点）
        for (int i = 0; i < nodes; i++) {
            graph.add(new ArrayList<>());
        }

        // 添加图的边（无向图）
        addEdge(0, 1);
        addEdge(0, 2);
        addEdge(1, 3);
        addEdge(1, 4);

        // 从节点 0 开始执行 BFS
        System.out.println("BFS:");
        bfs(0);
    }

    // 添加边的辅助方法，两个节点之间互相添加边（无向图）
    private static void addEdge(int from, int to) {
        graph.get(from).add(to);
        graph.get(to).add(from);
    }

    // 使用队列实现 BFS
    private static void bfs(int start) {
        // 创建一个队列来存储待访问的节点
        Queue<Integer> queue = new LinkedList<>();

        // 将起始节点加入队列
        queue.offer(start);
        // 标记起始节点为已访问
        visited[start] = true;

        // 当队列不为空时，循环执行 BFS
        while (!queue.isEmpty()) {
            // 取出队列的第一个节点，并将其标记为已访问
            int node = queue.poll();
            System.out.print(node + " ");  // 输出当前节点

            // 遍历当前节点的所有邻接节点
            for (int neighbor : graph.get(node)) {
                // 如果邻接节点未被访问过，则加入队列
                if (!visited[neighbor]) {
                    queue.offer(neighbor);  // 将未访问的邻接节点加入队列
                    visited[neighbor] = true;  // 标记该邻接节点为已访问
                }
            }
        }
    }
}

输出：

BFS Traversal: 0 1 2 3

五、DFS 和 BFS 的对比

深度优先搜索（DFS）和广度优先搜索（BFS）是解决图遍历问题的两种核心算法，但它们在实现原理、性能及适用场景上有所不同：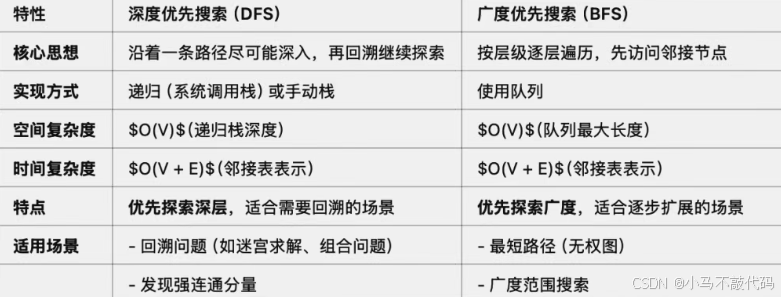

六、实际应用案例

1. 迷宫求解：DFS 回溯

迷宫求解是典型的 DFS 应用场景，通过递归尝试所有路径，直到找到目标。

问题描述：

在二维迷宫（矩阵），起点是 (0,0)，终点是 (N-1, M-1)。迷宫中 ‘0’ 表示可以走，‘1’ 表示障碍。找到一条通路（如果存在）。

public class MazeSolver {

    // dx 和 dy 数组用于存储四个方向的移动
    // dx: 上下左右的横坐标增量
    // dy: 上下左右的纵坐标增量
    private static final int[] dx = {-1, 1, 0, 0}; // 上、下、左、右
    private static final int[] dy = {0, 0, -1, 1}; // 上、下、左、右

    /**
     * 递归求解迷宫，返回是否存在通路
     * @param maze 迷宫的二维数组
     * @param x 当前的横坐标
     * @param y 当前的纵坐标
     * @param path 记录路径的二维数组
     * @return 如果找到路径返回 true，否则返回 false
     */
    public static boolean solveMaze(int[][] maze, int x, int y, int[][] path) {

        int n = maze.length; // 获取迷宫的行数
        int m = maze[0].length; // 获取迷宫的列数

        // 如果到达终点（右下角）
        if (x == n - 1 && y == m - 1) {
            path[x][y] = 1; // 标记当前节点为路径的一部分
            return true; // 返回 true，表示路径找到
        }

        // 如果当前移动有效，继续探索
        if (isValidMove(maze, x, y)) {
            path[x][y] = 1; // 标记当前节点为路径的一部分

            // 探索四个方向：上、下、左、右
            for (int i = 0; i < 4; i++) {
                int newX = x + dx[i]; // 计算新的横坐标
                int newY = y + dy[i]; // 计算新的纵坐标

                // 递归调用，尝试从新位置开始继续求解
                if (solveMaze(maze, newX, newY, path)) {
                    return true; // 如果递归找到路径，直接返回
                }
            }

            // 如果四个方向都没有找到路径，回溯，将当前节点标记为 0
            path[x][y] = 0; // 回溯
        }

        return false; // 如果没有找到路径，返回 false
    }

    /**
     * 判断当前位置 (x, y) 是否是有效的移动
     * @param maze 迷宫的二维数组
     * @param x 当前的横坐标
     * @param y 当前的纵坐标
     * @return 如果当前位置有效且未被访问，返回 true
     */
    private static boolean isValidMove(int[][] maze, int x, int y) {
        return x >= 0 && x < maze.length && y >= 0 && y < maze[0].length && maze[x][y] == 0;
        // 检查 (x, y) 是否在迷宫范围内，并且当前位置为 0（表示可通行）
    }

    public static void main(String[] args) {

        // 迷宫的示例，0 表示可通行，1 表示障碍
        int[][] maze = {
            {0, 1, 0, 0},
            {0, 0, 1, 0},
            {1, 0, 0, 0},
            {0, 1, 0, 0}
        };

        // 用于记录路径的二维数组，1 表示路径，0 表示没有走过
        int[][] path = new int[maze.length][maze[0].length];

        // 从 (0, 0) 开始求解迷宫
        if (solveMaze(maze, 0, 0, path)) {
            System.out.println("Path found:");

            // 打印路径，1 表示路径，0 表示没有走过
            for (int[] row : path) {
                for (int cell : row) {
                    System.out.print(cell + " ");
                }
                System.out.println();
            }
        } else {
            System.out.println("No path found.");
        }
    }
}

输出：

Path found:  
1 0 0 0  
1 1 0 0  
0 1 1 0  
0 0 1 0  

2. 最短路径：BFS 搜索

广度优先搜索可以用来在无权图中求最短路径。例如，从起点找到目标节点的最短步数。

问题描述：

在二维迷宫中，从起点到终点找到最短路径。

import java.util.*;

public class ShortestPath {

    // dx 和 dy 数组用于存储四个方向的移动
    // dx: 上下左右的横坐标增量
    // dy: 上下左右的纵坐标增量
    private static final int[] dx = {-1, 1, 0, 0}; // 上、下、左、右
    private static final int[] dy = {0, 0, -1, 1}; // 上、下、左、右

    /**
     * 使用 BFS 算法求解迷宫的最短路径
     * @param maze 迷宫的二维数组，0 表示可通行，1 表示障碍
     * @param startX 起点横坐标
     * @param startY 起点纵坐标
     * @param endX 终点横坐标
     * @param endY 终点纵坐标
     * @return 返回起点到终点的最短路径长度，如果不可达返回 -1
     */
    public static int findShortestPath(int[][] maze, int startX, int startY, int endX, int endY) {

        int n = maze.length; // 获取迷宫的行数
        int m = maze[0].length; // 获取迷宫的列数

        // 使用队列进行 BFS 搜索
        Queue<int[]> queue = new LinkedList<>();
        // 记录每个位置是否被访问过，防止重复访问
        boolean[][] visited = new boolean[n][m];

        // 将起点加入队列，初始距离为 0
        queue.add(new int[]{startX, startY, 0}); // {x, y, distance}
        visited[startX][startY] = true; // 标记起点为已访问

        // BFS 搜索过程
        while (!queue.isEmpty()) {
            // 获取队列中的第一个元素
            int[] current = queue.poll();
            int x = current[0], y = current[1], dist = current[2]; // 获取当前位置 (x, y) 和当前距离

            // 如果到达终点，返回当前路径长度
            if (x == endX && y == endY) {
                return dist; // 返回从起点到终点的最短距离
            }

            // 探索四个方向：上、下、左、右
            for (int i = 0; i < 4; i++) {
                int newX = x + dx[i]; // 计算新的横坐标
                int newY = y + dy[i]; // 计算新的纵坐标

                // 如果新位置有效，加入队列
                if (isValidMove(maze, newX, newY, visited)) {
                    // 将新位置加入队列，距离 +1
                    queue.add(new int[]{newX, newY, dist + 1});
                    visited[newX][newY] = true; // 标记新位置为已访问
                }
            }
        }

        // 如果队列为空，表示无法到达终点，返回 -1
        return -1;
    }

    /**
     * 判断当前位置 (x, y) 是否为有效的移动
     * @param maze 迷宫的二维数组
     * @param x 当前的横坐标
     * @param y 当前的纵坐标
     * @param visited 记录每个位置是否被访问的数组
     * @return 如果当前位置有效且未被访问，返回 true
     */
    private static boolean isValidMove(int[][] maze, int x, int y, boolean[][] visited) {
        // 判断是否越界、是否为障碍物且是否已经访问过
        return x >= 0 && x < maze.length && y >= 0 && y < maze[0].length && maze[x][y] == 0 && !visited[x][y];
    }

    public static void main(String[] args) {

        // 迷宫的示例，0 表示可通行，1 表示障碍
        int[][] maze = {
            {0, 1, 0, 0},
            {0, 0, 1, 0},
            {1, 0, 0, 0},
            {0, 1, 0, 0}
        };

        // 调用 findShortestPath 方法求解最短路径
        int shortestPath = findShortestPath(maze, 0, 0, 3, 2);

        // 输出最短路径长度
        if (shortestPath != -1) {
            System.out.println("Shortest path length: " + shortestPath);
        } else {
            System.out.println("No path found.");
        }
    }
}

输出：

在迷宫中：

0 1 0 0
0 0 1 0
1 0 0 0
0 1 0 0

从起点(0, 0)到终点(3, 2)，最短路径经过的节点是：

• (0, 0)→(1, 0)→(1, 1)→(2, 1)→(3, 1)→(3, 2)

共计 5 步。因此，最短路径长度是 5。

Shortest path length: 5

六、总结

1.DFS 与栈：递归依赖系统调用栈，手动实现可用Stack或ArrayDeque。

2.BFS 与队列：需要使用Queue接口（如LinkedList或ArrayDeque）管理节点。

3.应用场景：

• DFS：适合回溯问题（如迷宫求解）。

• BFS：适合逐层扩展问题（如无权图的最短路径）。