归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。作为一种典型的分而治之思想的算法应用，归并排序的实现由两种方法：

  • 自上而下的递归（所有递归的方法都可以用迭代重写，所以就有了第 2 种方法）；
  • 自下而上的迭代；

        在《数据结构与算法 JavaScript 描述》中，作者给出了自下而上的迭代方法。但是对于递归法，作者却认为：

However, it is not possible to do so in JavaScript, as the recursion goes too deep for the language to handle.

然而，在 JavaScript 中这种方式不太可行，因为这个算法的递归深度对它来讲太深了。

        和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。归并排序的核心思想是将一个大问题分解成若干个小问题，分别解决这些小问题，然后将结果合并起来，最终得到整个问题的解。

具体到排序问题，归并排序的步骤如下：

  1. 分解（Divide）：将待排序的数组分成两个子数组，每个子数组包含大约一半的元素。
  2. 解决（Conquer）：递归地对每个子数组进行排序。
  3. 合并（Combine）：将两个已排序的子数组合并成一个有序的数组。

通过不断地分解和合并，最终整个数组将被排序。

一、分治

        顾名思义，分而治之。

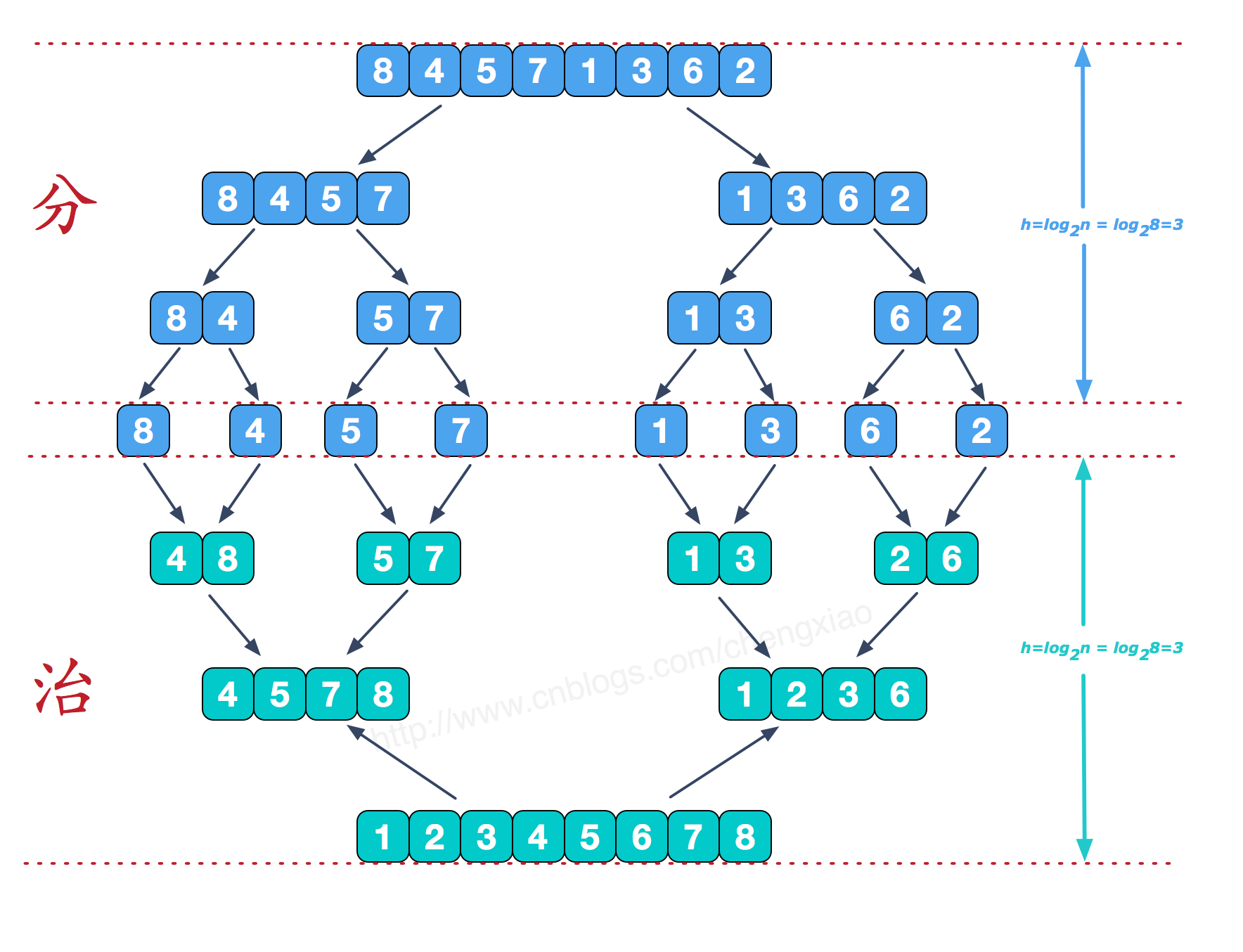
        可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

合并相邻有序子序列

        再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

 

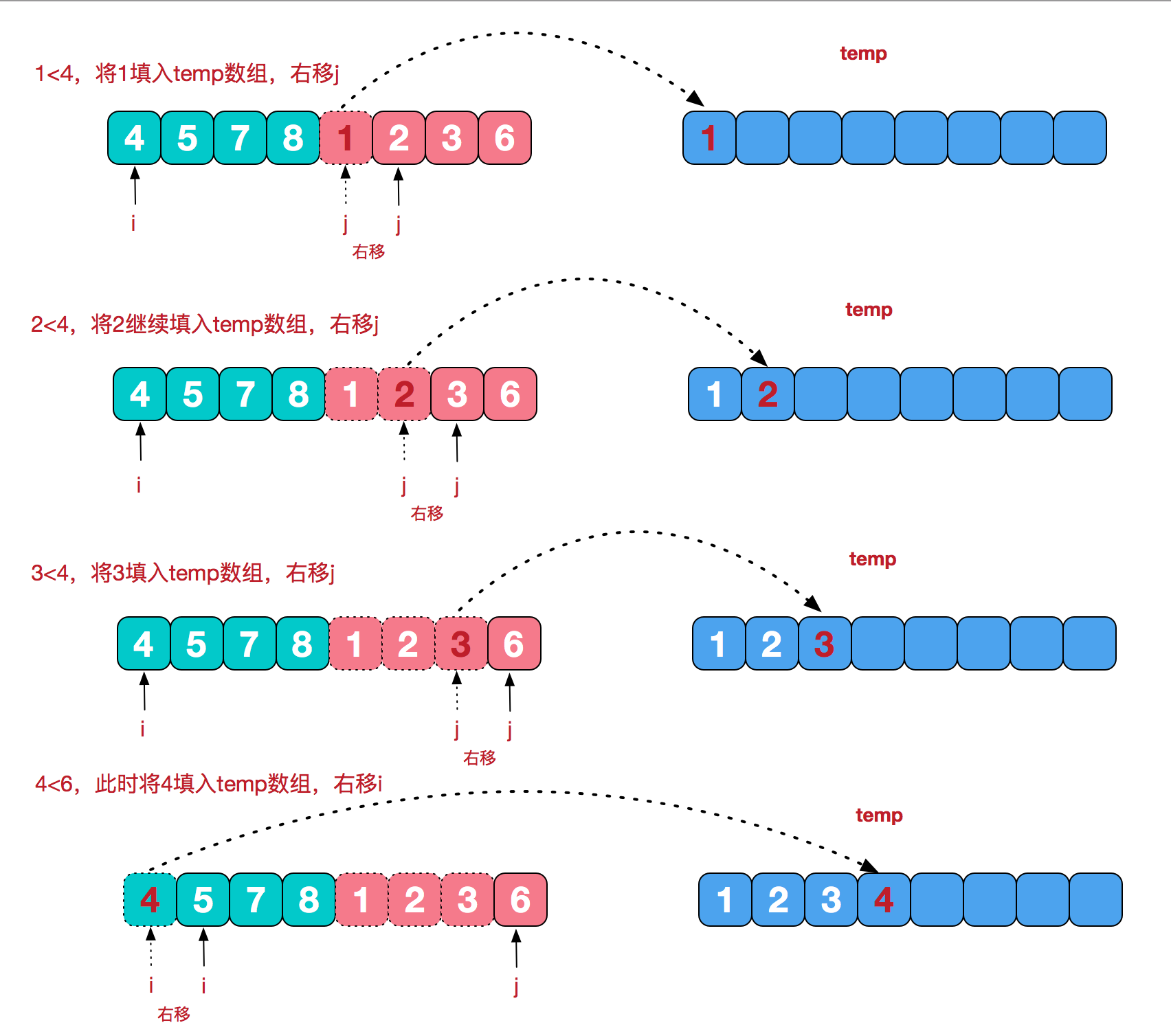
二、算法步骤

  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；

  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

  4. 重复步骤 3 直到某一指针达到序列尾；

  5. 将另一序列剩下的所有元素直接复制到合并序列尾。 

三、动图演示

 

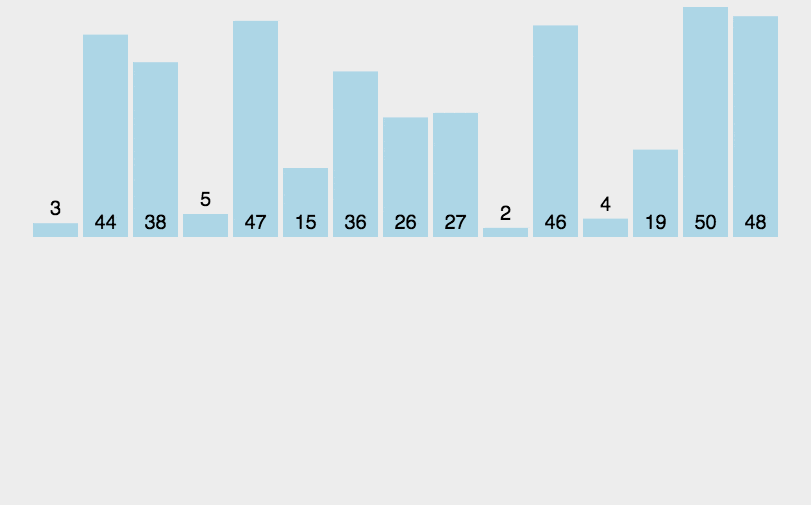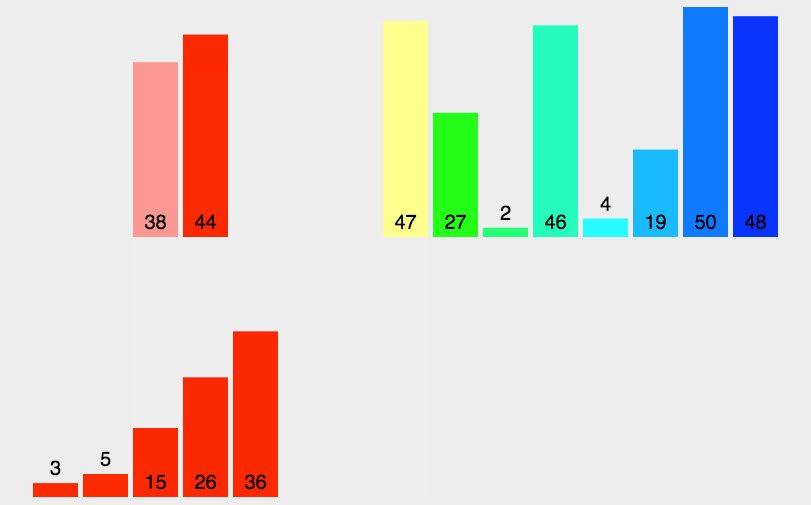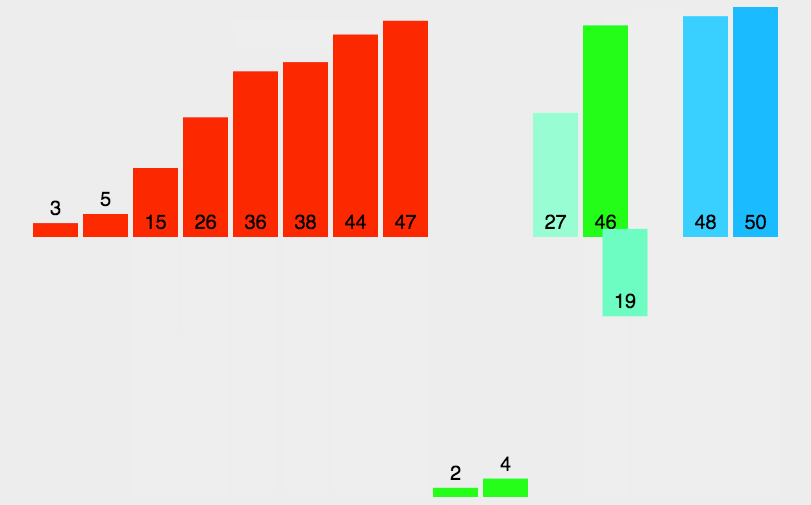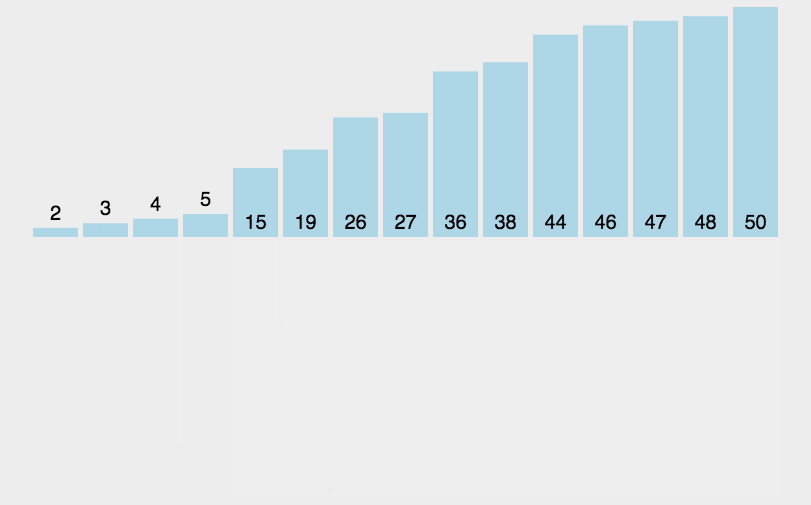
假设有一个待排序的列表 [38, 27, 43, 3, 9, 82, 10]，归并排序的过程如下：

  1. 分解：

    • 将列表分成两半：[38, 27, 43, 3] 和 [9, 82, 10]。

    • 继续分解：

      • [38, 27, 43, 3] 分成 [38, 27] 和 [43, 3]。

      • [9, 82, 10] 分成 [9] 和 [82, 10]。

    • 继续分解：

      • [38, 27] 分成 [38] 和 [27]。

      • [43, 3] 分成 [43] 和 [3]。

      • [82, 10] 分成 [82] 和 [10]。

    • 最终分解为单个元素的子列表。

  2. 合并：

    • 合并 [38] 和 [27] 得到 [27, 38]。

    • 合并 [43] 和 [3] 得到 [3, 43]。

    • 合并 [27, 38] 和 [3, 43] 得到 [3, 27, 38, 43]。

    • 合并 [9] 和 [10, 82] 得到 [9, 10, 82]。

    • 合并 [3, 27, 38, 43] 和 [9, 10, 82] 得到最终有序列表 [3, 9, 10, 27, 38, 43, 82]。

 四、代码实现 

       实例

def merge_sort(arr):
    if len(arr) <= 1:
        return arr

    # 分解：将列表分成两半
    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])  # 递归排序左半部分
    right_half = merge_sort(arr[mid:])  # 递归排序右半部分

    # 合并：将两个有序子列表合并
    return merge(left_half, right_half)

def merge(left, right):
    sorted_arr = []
    i = j = 0

    # 比较两个子列表的元素，按顺序合并
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            sorted_arr.append(left[i])
            i += 1
        else:
            sorted_arr.append(right[j])
            j += 1

    # 将剩余的元素添加到结果中
    sorted_arr.extend(left[i:])
    sorted_arr.extend(right[j:])
    return sorted_arr

# 示例
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = merge_sort(arr)
print(sorted_arr)  # 输出: [3, 9, 10, 27, 38, 43, 82]

        JavaScript

function mergeSort(arr) {  // 采用自上而下的递归方法
    var len = arr.length;
    if(len < 2) {
        return arr;
    }
    var middle = Math.floor(len / 2),
        left = arr.slice(0, middle),
        right = arr.slice(middle);
    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right)
{
    var result = [];

    while (left.length && right.length) {
        if (left[0] <= right[0]) {
            result.push(left.shift());
        } else {
            result.push(right.shift());
        }
    }

    while (left.length)
        result.push(left.shift());

    while (right.length)
        result.push(right.shift());

    return result;
}

        Python

def mergeSort(arr):
    import math
    if(len(arr)<2):
        return arr
    middle = math.floor(len(arr)/2)
    left, right = arr[0:middle], arr[middle:]
    return merge(mergeSort(left), mergeSort(right))

def merge(left,right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0));
    while left:
        result.append(left.pop(0))
    while right:
        result.append(right.pop(0));
    return result

        Go

func mergeSort(arr []int) []int {
        length := len(arr)
        if length < 2 {
                return arr
        }
        middle := length / 2
        left := arr[0:middle]
        right := arr[middle:]
        return merge(mergeSort(left), mergeSort(right))
}

func merge(left []int, right []int) []int {
        var result []int
        for len(left) != 0 && len(right) != 0 {
                if left[0] <= right[0] {
                        result = append(result, left[0])
                        left = left[1:]
                } else {
                        result = append(result, right[0])
                        right = right[1:]
                }
        }

        for len(left) != 0 {
                result = append(result, left[0])
                left = left[1:]
        }

        for len(right) != 0 {
                result = append(result, right[0])
                right = right[1:]
        }

        return result
}

        Java

public class MergeSort implements IArraySort {

    @Override
    public int[] sort(int[] sourceArray) throws Exception {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        if (arr.length < 2) {
            return arr;
        }
        int middle = (int) Math.floor(arr.length / 2);

        int[] left = Arrays.copyOfRange(arr, 0, middle);
        int[] right = Arrays.copyOfRange(arr, middle, arr.length);

        return merge(sort(left), sort(right));
    }

    protected int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        int i = 0;
        while (left.length > 0 && right.length > 0) {
            if (left[0] <= right[0]) {
                result[i++] = left[0];
                left = Arrays.copyOfRange(left, 1, left.length);
            } else {
                result[i++] = right[0];
                right = Arrays.copyOfRange(right, 1, right.length);
            }
        }

        while (left.length > 0) {
            result[i++] = left[0];
            left = Arrays.copyOfRange(left, 1, left.length);
        }

        while (right.length > 0) {
            result[i++] = right[0];
            right = Arrays.copyOfRange(right, 1, right.length);
        }

        return result;
    }

}

        PHP

function mergeSort($arr)
{
    $len = count($arr);
    if ($len < 2) {
        return $arr;
    }
    $middle = floor($len / 2);
    $left = array_slice($arr, 0, $middle);
    $right = array_slice($arr, $middle);
    return merge(mergeSort($left), mergeSort($right));
}

function merge($left, $right)
{
    $result = [];

    while (count($left) > 0 && count($right) > 0) {
        if ($left[0] <= $right[0]) {
            $result[] = array_shift($left);
        } else {
            $result[] = array_shift($right);
        }
    }

    while (count($left))
        $result[] = array_shift($left);

    while (count($right))
        $result[] = array_shift($right);

    return $result;
}

        C

int min(int x, int y) {
    return x < y ? x : y;
}
void merge_sort(int arr[], int len) {
    int *a = arr;
    int *b = (int *) malloc(len * sizeof(int));
    int seg, start;
    for (seg = 1; seg < len; seg += seg) {
        for (start = 0; start < len; start += seg * 2) {
            int low = start, mid = min(start + seg, len), high = min(start + seg * 2, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        int *temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        int i;
        for (i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    free(b);
}

递归：

void merge_sort_recursive(int arr[], int reg[], int start, int end) {
    if (start >= end)
        return;
    int len = end - start, mid = (len >> 1) + start;
    int start1 = start, end1 = mid;
    int start2 = mid + 1, end2 = end;
    merge_sort_recursive(arr, reg, start1, end1);
    merge_sort_recursive(arr, reg, start2, end2);
    int k = start;
    while (start1 <= end1 && start2 <= end2)
        reg[k++] = arr[start1] < arr[start2] ? arr[start1++] : arr[start2++];
    while (start1 <= end1)
        reg[k++] = arr[start1++];
    while (start2 <= end2)
        reg[k++] = arr[start2++];
    for (k = start; k <= end; k++)
        arr[k] = reg[k];
}

void merge_sort(int arr[], const int len) {
    int reg[len];
    merge_sort_recursive(arr, reg, 0, len - 1);
}

        C++

迭代：

template<typename T> // 整數或浮點數皆可使用,若要使用物件(class)時必須設定"小於"(<)的運算子功能
void merge_sort(T arr[], int len) {
    T *a = arr;
    T *b = new T[len];
    for (int seg = 1; seg < len; seg += seg) {
        for (int start = 0; start < len; start += seg + seg) {
            int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
            int k = low;
            int start1 = low, end1 = mid;
            int start2 = mid, end2 = high;
            while (start1 < end1 && start2 < end2)
                b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
            while (start1 < end1)
                b[k++] = a[start1++];
            while (start2 < end2)
                b[k++] = a[start2++];
        }
        T *temp = a;
        a = b;
        b = temp;
    }
    if (a != arr) {
        for (int i = 0; i < len; i++)
            b[i] = a[i];
        b = a;
    }
    delete[] b;
}

递归：

void Merge(vector<int> &Array, int front, int mid, int end) {
    // preconditions:
    // Array[front...mid] is sorted
    // Array[mid+1 ... end] is sorted
    // Copy Array[front ... mid] to LeftSubArray
    // Copy Array[mid+1 ... end] to RightSubArray
    vector<int> LeftSubArray(Array.begin() + front, Array.begin() + mid + 1);
    vector<int> RightSubArray(Array.begin() + mid + 1, Array.begin() + end + 1);
    int idxLeft = 0, idxRight = 0;
    LeftSubArray.insert(LeftSubArray.end(), numeric_limits<int>::max());
    RightSubArray.insert(RightSubArray.end(), numeric_limits<int>::max());
    // Pick min of LeftSubArray[idxLeft] and RightSubArray[idxRight], and put into Array[i]
    for (int i = front; i <= end; i++) {
        if (LeftSubArray[idxLeft] < RightSubArray[idxRight]) {
            Array[i] = LeftSubArray[idxLeft];
            idxLeft++;
        } else {
            Array[i] = RightSubArray[idxRight];
            idxRight++;
        }
    }
}

void MergeSort(vector<int> &Array, int front, int end) {
    if (front >= end)
        return;
    int mid = (front + end) / 2;
    MergeSort(Array, front, mid);
    MergeSort(Array, mid + 1, end);
    Merge(Array, front, mid, end);
}

        C#

public static List<int> sort(List<int> lst) {
    if (lst.Count <= 1)
        return lst;
    int mid = lst.Count / 2;
    List<int> left = new List<int>();  // 定义左侧List
    List<int> right = new List<int>(); // 定义右侧List
    // 以下兩個循環把 lst 分為左右兩個 List
    for (int i = 0; i < mid; i++)
        left.Add(lst[i]);
    for (int j = mid; j < lst.Count; j++)
        right.Add(lst[j]);
    left = sort(left);
    right = sort(right);
    return merge(left, right);
}
/// <summary>
/// 合併兩個已經排好序的List
/// </summary>
/// <param name="left">左側List</param>
/// <param name="right">右側List</param>
/// <returns></returns>
static List<int> merge(List<int> left, List<int> right) {
    List<int> temp = new List<int>();
    while (left.Count > 0 && right.Count > 0) {
        if (left[0] <= right[0]) {
            temp.Add(left[0]);
            left.RemoveAt(0);
        } else {
            temp.Add(right[0]);
            right.RemoveAt(0);
        }
    }
    if (left.Count > 0) {
        for (int i = 0; i < left.Count; i++)
            temp.Add(left[i]);
    }
    if (right.Count > 0) {
        for (int i = 0; i < right.Count; i++)
            temp.Add(right[i]);
    }
    return temp;
}

递归：

//归并排序算法类
class MergeTest
{
    //方法-：归并排序的如果，提供了辅助数组，调用了后续方法
    public void MergeSort(float[] arr)
    {
        if( arr.Length <= 1 ) return;

        float[] temp = new float[arr.Length];  //辅助数组

        if (temp != null)  MSort(arr, temp, 0, arr.Length - 1);  //调用递归拆分
       
    }


    //方法二： 递归拆分数组 ，并且调用合并的方法
    private void MSort(float[] arr , float[] temp ,int left , int right)  
    {
        if( left < right) //最终会使得递归得到一个元素为一组的多数组
        {
            int mid = (left+right)/2;  //left为原数组左边第一个元素下标（就是0），right是原数组右边最大下标（n-1）,mid用于拆分数组

            MSort(arr, temp, left, mid); //通过递归划分左半区
            MSort(arr, temp, mid+1, right);  //递归划分右半区

            Merge(arr, temp, left, mid, right); //调用排序并合并的方法
        }
    }

    //方法三：排序合并拆分的数组
    private void Merge(float[] arr, float[] temp , int left , int mid , int right)
    {
        int l_pos = left;  //左半区第一个未排序的元素
        int r_pos = mid + 1; //右半区第一个未排序的元素
        int pos = left;  //辅助数组的起点下标

        while(l_pos <= mid && r_pos <= right)
        {
            if(arr[l_pos] < arr[r_pos])   //逐一比较大小
            {
                temp[pos++] = arr[l_pos++]; //左边区域元素更小，就把它放入辅助数组的第一个位置，然后左边区域与辅助数组的下标向后移动一位
            }
            else temp[pos++] = arr[r_pos++]; //若右边区域元素更小，将其放入辅助数组，下标后移

        } //跳出循环就代表左右中的一边已经全部放入辅助数组了

        while( l_pos <= mid)
        {
            temp[pos++] = arr[l_pos++]; //若左区域下标还没有到达最大处，说明有剩余，直接全部复制到辅助数组最后边
        }
        while( r_pos <= right)
        {
            temp[pos++] = arr[r_pos++];//若右区域下标还没有到达最大处，说明有剩余，直接全部复制到辅助数组最后边
        }

        while(left <= right)
        {
            arr[left] = temp[left];  //从第一个下标到最后一个下标，把辅助数组的元素全部复制到原来的数组z

            left++;
        }
    }
}

        Rust

fn merge_sort<T: Ord + Debug + Copy>(array: &mut [T], start: usize, end: usize) {    
    if start >= end {        
        return;    
    }    
    let mid = start + (end - start) / 2;    
    merge_sort(array, start, mid);    
    merge_sort(array, mid + 1, end);    
    merge(array, start, end);
}

fn merge<T: Ord + Debug + Copy>(array: &mut [T], start: usize, end: usize) {    
    println!("{array:?}");    
    let mut temp_array = Vec::with_capacity(end - start + 1);    
    for i in start..=end {        
        temp_array.push(array[i]);    
    }    
    let new_start = 0;    
    let new_end = temp_array.len() - 1;    
    let new_mid = (new_end - new_start) / 2;    
    let mut left_index = new_start;    
    let mut right_index = new_mid + 1;    
    let mut array_index = start;    
    while left_index <= new_mid && right_index <= new_end {        
        if temp_array[left_index] <= temp_array[right_index] {            
            array[array_index] = temp_array[left_index];            
            left_index += 1;        
        } else {            
            array[array_index] = temp_array[right_index];            
            right_index += 1;        
        }        
        array_index += 1;    
    }    
    while left_index <= new_mid {        
        array[array_index] = temp_array[left_index];        
        left_index += 1;        
        array_index += 1;    
    }    
    while right_index <= new_end {        
        array[array_index] = temp_array[right_index];        
        right_index += 1;        
        array_index += 1;    
    }
}

        Ruby 

def merge list
  return list if list.size < 2

  pivot = list.size / 2

  # Merge
  lambda { |left, right|
    final = []
    until left.empty? or right.empty?
      final << if left.first < right.first; left.shift else right.shift end
    end
    final + left + right
  }.call merge(list[0...pivot]), merge(list[pivot..-1])
end

        Haskell 

merge' :: Ord a => [a] -> [a] -> [a]
merge' xs [] = xs
merge' [] xs = xs
merge' (x : xs) (y : ys)
  | x > y = y : merge' (x : xs) ys
  | otherwise = x : merge' xs (y : ys)

msort :: Ord a => [a] -> [a]
msort [] = []
msort [x] = [x]
msort xs = merge' (msort (take half_len xs)) (msort (drop half_len xs))
  where
    half_len = length xs `div` 2

 五、复杂度

1、时间复杂度

  • 分解：每次将列表分成两半，需要 O(log n) 层递归。

  • 合并：每层递归需要 O(n) 的时间来合并子列表。

  • 总时间复杂度：O(n log n)。

2、空间复杂度

  • O(n)，归并排序需要额外的空间来存储临时列表。

六、优缺点

  • 优点：

    • 时间复杂度稳定为 O(n log n)，适合大规模数据。

    • 稳定排序算法（相同元素的相对顺序不会改变）。

    • 适合外部排序（如对磁盘文件进行排序）。

  • 缺点：

    • 需要额外的存储空间，空间复杂度为 O(n)。

    • 对于小规模数据，性能可能不如插入排序等简单算法。

# 排序算法 # 算法 # 数据结构
Logo
魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

cover

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

avatar 魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。

avatar 魔乐社区
cover

小杰机器学习（seven）——贝叶斯分类

avatar 魔乐社区