左程云算法与数据结构代码汇总之排序（Java）
排序的代码汇总。（后续还需补充）
系列文章目录
左程云算法与数据结构代码汇总之链表（Java）-CSDN博客
目录
1.数组中，一个数出现了奇数次，其他数出现了偶数次，要找奇数次的数
2. 数组中，2个数a，b出现了奇数次，其他数出现了偶数次，要找奇数次的数
前言
排序的代码汇总。（后续还需补充）
一、排序种类
选择排序
第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。
public static void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr, i, minIndex);
}
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
时间复杂度为n^2 。
冒泡排序
相邻元素两两比较，大的右移，直到最大的数放到最后，结束一轮比较，再开始下一轮。
public static void bubbleSort(int[] arr){
if(arr==null||arr.length<2) return;
for(int e=arr.length-1;e>0;e--){
for(int i=0;i<e;i++){
if(arr[i]>arr[i+1]){
swap(arr,i,i+1);
}
}
}
}
public static void swap(int[] arr,int i,int j){
arr[i]=arr[i]^arr[j];
arr[j]=arr[i]^arr[j];
arr[i]=arr[i]^arr[j];
}这个地方的swap很有意思，就是说异或运算可以交换两数，但是如果在同一个存储位置就会变成0，谨慎使用最好还是用之前那个swap算法
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
异或运算
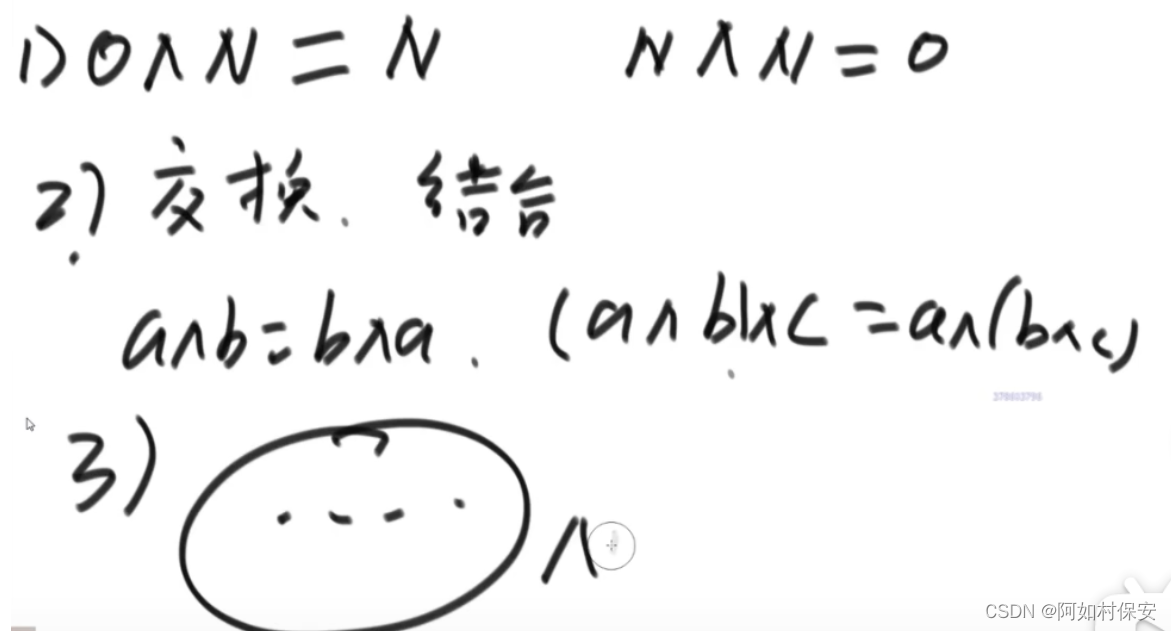
原数异或0等于本身，原数异或本身等于0。异或可以看作是无进位相加。
这里有两个题：
1.数组中，一个数出现了奇数次，其他数出现了偶数次，要找奇数次的数
将所有数都异或，最后只剩下奇数次的数。
public static void printOddTimesNum1(int[] arr) {
int eor = 0;
for (int cur : arr) {
eor ^= cur;
}
System.out.println(eor);
}
2. 数组中，2个数a，b出现了奇数次，其他数出现了偶数次，要找奇数次的数
将所有数都异或，得到eor=a^b；因为a！=b，所以eor！=0，必造成eor有一个位上为1，那个位就能用来区分a和b。
eor & (~eor + 1);//选出e0最右边的一个1，或者可以是eor && -eor （补码）
public static void printOddTimesNum2(int[] arr) {
int eO = 0, eOhasOne = 0;
for (int curNum : arr) {
eO ^= curNum;
}
int rightOne = eO & (~eO + 1);//选出e0最右边的一个1，
for (int cur : arr) {
if ((cur & rightOne) != 0) {
eOhasOne ^= cur;//最后得到的这个数，是这一个位上有1的数，与其他数的异或
}
}
System.out.println(eOhasOne + " " + (eO ^ eOhasOne));
}
插入排序
0~1范围有序；0~2范围有序，将第二个位置的数插入到前面，排好序就停下，所以比较的次数与数据的结构有关；依次。。。到最后一个停下。
public static void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; i++) {
//判断条件，j >= 0：换到最后就停，arr[j] > arr[j + 1]排好序就停
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
swap(arr, j, j + 1);
}
}
}
public static void swap(int[] arr, int i, int j) {
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
递归排序
类似于二叉树，由上往下，不断进栈，每一条叉都会进栈出栈，实现遍历。三道题套路解决递归问题 | lyl's blog (lyl0724.github.io)
用位运算会快一点。
public static int getMax(int[] arr) {
return process(arr, 0, arr.length - 1);
}
public static int process(int[] arr, int L, int R) {
if (L == R) {
return arr[L];
}
int mid = L + ((R - L) >> 1);
int leftMax = process(arr, L, mid);
int rightMax = process(arr, mid + 1, R);
return Math.max(leftMax, rightMax);
}
对于递归的时空复杂度可以用master公式去判断：
master公式
母问题可以用下面的式子表示的，子问题的规模要一致，子问题是母问题的B分之1，调用a次子问题，第二项是其他的复杂度。
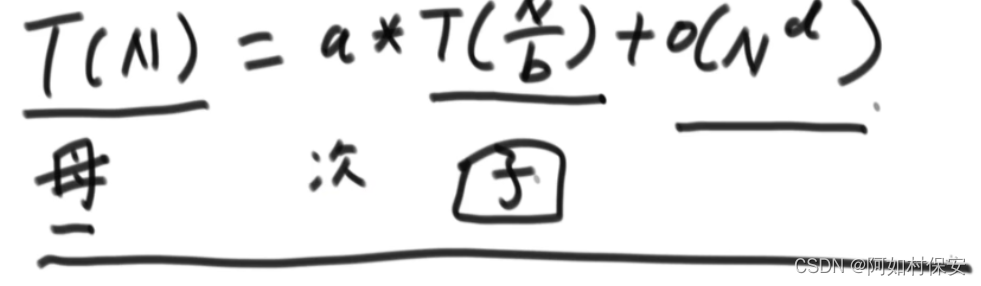
log(b, a) 指的是以底数 b 计算 a 的对数。
归并排序
归并排序和快速排序是比较高效的排序算法。
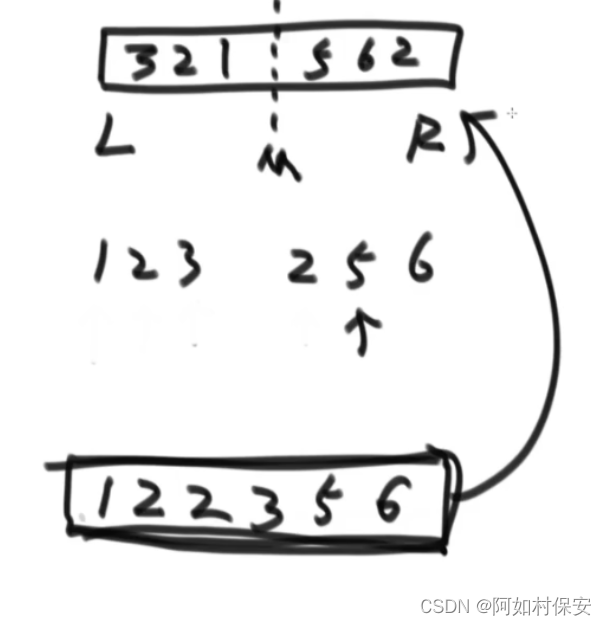
分治法。将n个元素从中间切开，分成两部分。两边都各自排序好，然后依次比较大小，合并进一个新数组。(左边可能比右边多1个数) 将左边和右边分成的两部分,再分别进行递归分解。 从最底层开始逐步合并两个排好序的数列。
public static void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);
mergeSort(arr, mid + 1, r);
merge(arr, l, mid, r);
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {//一直往help里面黏贴，同时p1或p2指针一直右移直至越界
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {//把没越界的指针后面剩余的数组黏贴到help里面
help[i++] = arr[p1++];
}
while (p2 <= r) {//把没越界的指针后面剩余的数组黏贴到help里面
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {//把排好序的help数组黏贴到原始数组的位置
arr[l + i] = help[i];
}
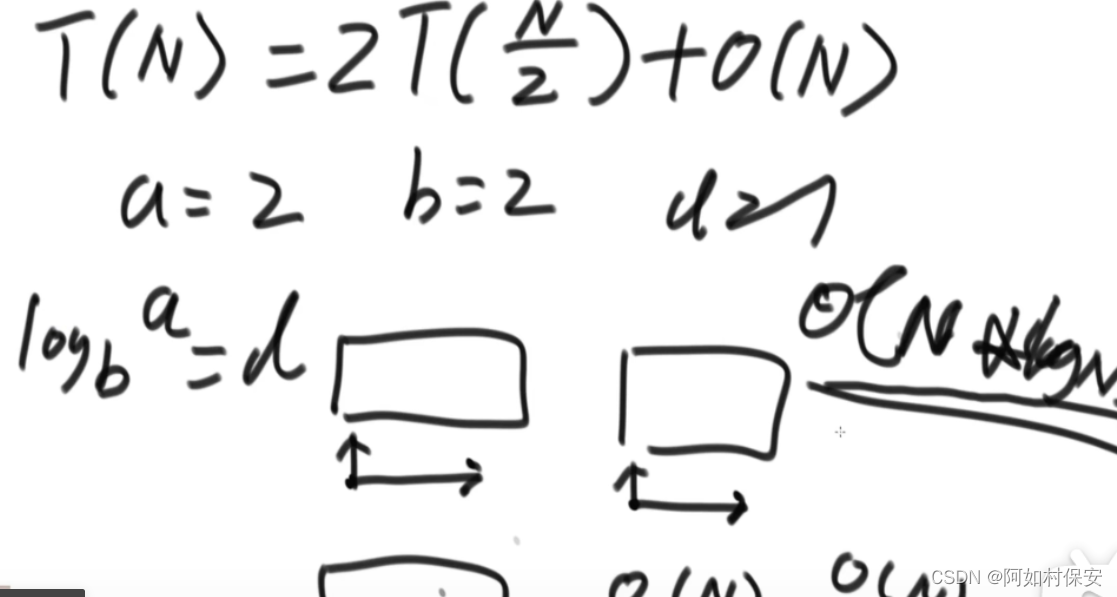
子问题mergeSort的规模都是N/2，merge的复杂度是N，母问题的复杂度为 O ( N ∗ log N ) + O ( N ) 。选择排序，冒泡排序，插入排序，都是有大量重复的比较，浪费了比较的信息，而归并排序，用空间换了时间，每次比较都没有被浪费，每次比较都进行排序，所以复杂度低。
小和问题
1.直接遍历，复杂度O（N的平方）
2.算一个数，右边有多少个数比他大：比1大有4个，比3大有2个…
其实就是在递归合并里面加了一行代码，计算右边数组中，有多少个数比p1指针所指的数要大。
public static int smallSum(int[] arr) {
if (arr == null || arr.length < 2) {
return 0;
}
return mergeSort(arr, 0, arr.length - 1);
}
public static int mergeSort(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int mid = l + ((r - l) >> 1);
return mergeSort(arr, l, mid) //左侧排序求小和
+ mergeSort(arr, mid + 1, r) //右侧侧排序求小和
+ merge(arr, l, mid, r);//2侧排序求小和
}
public static int merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;//记录右边的数组有几个数比左边当前数要大
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];//一直往help里面黏贴，同时p1或p2指针一直右移直至越界，将2个数组合并重排
}
while (p1 <= m) {//把没越界的指针后面剩余的数组黏贴到help里面
help[i++] = arr[p1++];
}
while (p2 <= r) {//把没越界的指针后面剩余的数组黏贴到help里面
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {//把排好序的help数组黏贴到原始数组的位置
arr[l + i] = help[i];
}
return res;
}逆序对问题（待补充）
在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请打印所有逆序对。
只要涉及数组中，两两比较，再进行操作的，都可以用归并排序。
快速排序
基于分治的思想，通过不断将数组划分成较小和较大的两部分，然后分别对这两部分进行排序，最终实现整个数组的排序。
quickSort 函数递归地将数组分成较小和较大的两部分，然后调用 partition 函数来找到一个枢纽元素（通常是数组的最后一个元素），并将数组分成两部分，使得左边的元素都比枢纽元素小，右边的元素都比枢纽元素大。这样就实现了快速排序。
随机选择一个数来划分，那个极端好和极端坏的情况都是等概率事件，复杂度与概率求期望，得到期望复杂度为 O ( N log N )
public static void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int l, int r) {
if (l < r) {
//将末位数字随机打乱
swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
int[] p = partition(arr, l, r);
quickSort(arr, l, p[0] - 1);
quickSort(arr, p[1] + 1, r);
}
}
public static int[] partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr, ++less, l++);//把当前数归到less区域
} else if (arr[l] > arr[r]) {
swap(arr, --more, l);//把当前数归到more区域
} else {
l++;//推着equal区域右移
}
}
swap(arr, more, r);//把num放到equal区域
return new int[] { less + 1, more };//返回less区域和equal区域的边界，equal区域和more区域的边界
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
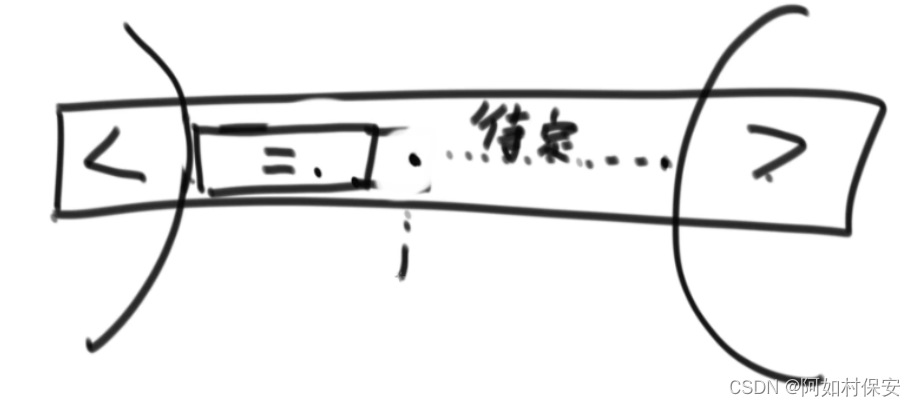
荷兰国旗问题1
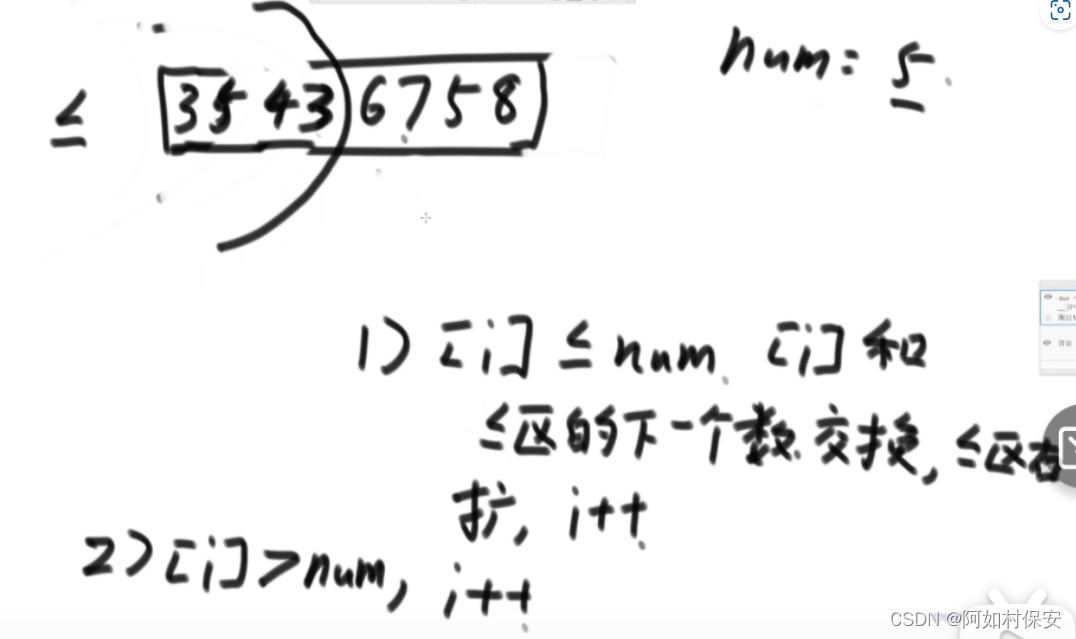
小于区域不断往右扩展，遇到比num大的数，就与未比较的区域的数交换，把大于num的数扔到右边，直到小于区域与右边的大于区域相遇。
荷兰国旗问题2
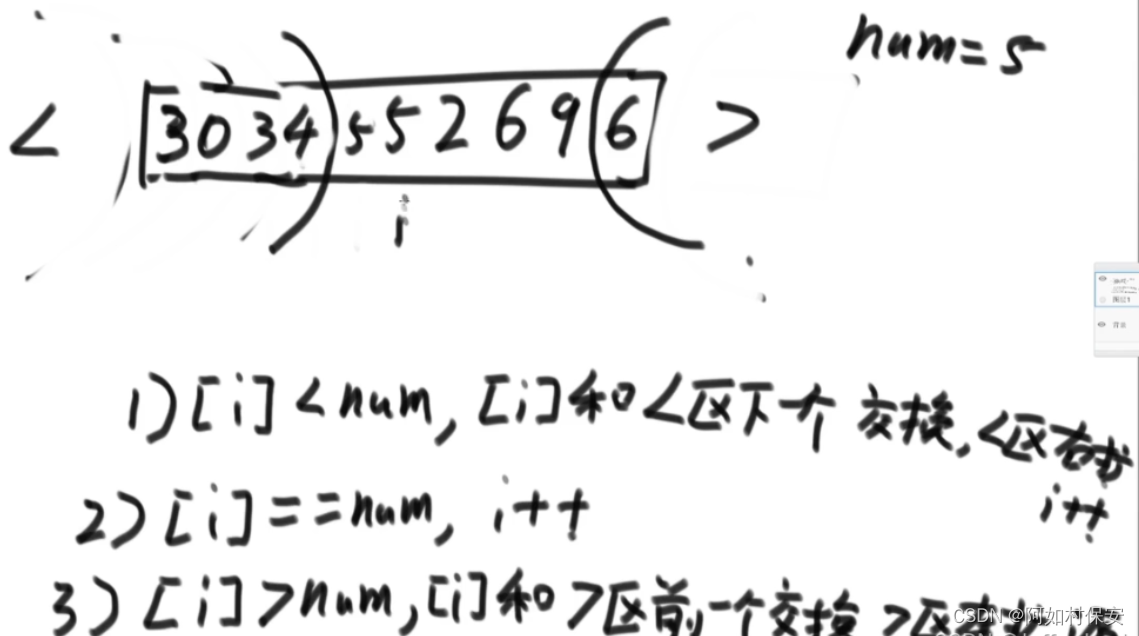小于区域推着等于区域走。
堆排序
新进堆的数（i）与父节点（（i-1）/2）比较，形成大根堆
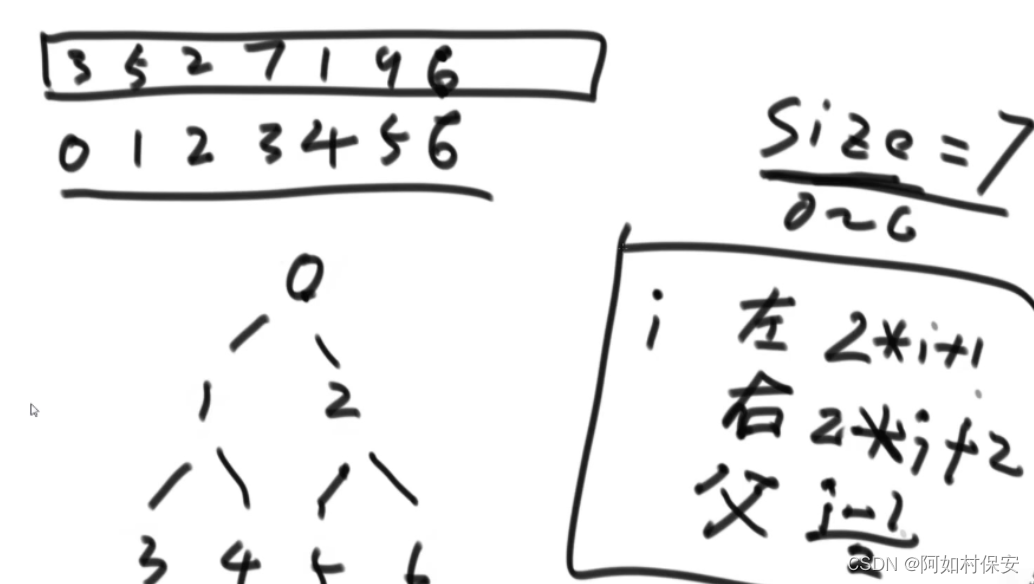
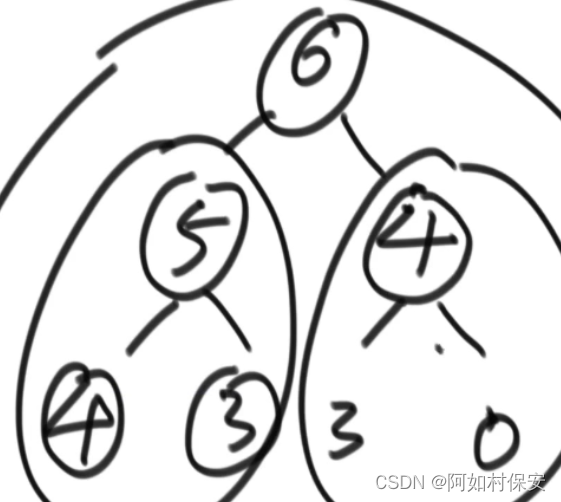
把新的数插入到堆中，就是上移（heapInsert）：
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {//当前节点数值大于父节点位置
swap(arr, index, (index - 1) /2);
index = (index - 1)/2 ;
}
}
某数a在index位置，将其往下移动，至堆结构符合大根堆要求，就是下移（heapify）：
//某数a在index位置，将其往下移动
public static void heapify(int[] arr, int index, int size) {//size为数组长度
int left = index * 2 + 1;//左孩子位置
while (left < size) {//判断孩子是否存在
//只有当右孩子存在且大于左孩子时，才取右孩子作为最大值；
//其余情况选左孩子，包括
// 1.右孩子不存在
// 2.右孩子存在但没左孩子大
//largest记录最大值的位置
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
//比较父节点和大孩子之间谁大，记录下大的值的位置
largest = arr[largest] > arr[index] ? largest : index;
//如果父节点比较大，堆结构排好，退出
if (largest == index) {
break;
}
//孩子比较大，交换父和孩子的位置
swap(arr, largest, index);
//记录某数a的新位置
index = largest;
//记录处于新位置的某数a的左孩子
left = index * 2 + 1;
}
}
新增一个数，或删除最大值，调整的复杂度都是 O ( log N )。
大根堆
用大根堆来排序：
所有数字先入大根堆，然后将最大数字于heapsize最后一个元素交换，heapsize减一，然后第一个数做heapify的下移操作，如此反复，就能将全部数字排序（升序），调整的复杂度都是 O ( N log N ) 。
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
//将所有数字搞成大根堆
for (int i = 0; i < arr.length; i++) {// O(N)
heapInsert(arr, i);// O(logN)
}
int size = arr.length;
//0位置上的数与heapsize最后一个数交换
swap(arr, 0, --size);
while (size > 0) {// O(N)
//0位置上的数重新调整位置
heapify(arr, 0, size);// O(logN)
//0位置上的数与heapsize最后一个数交换,heapsize减小
swap(arr, 0, --size);// O(1)
}
}
public static void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
//将所有数字搞成大根堆
//做法1：
// for (int i = 0; i < arr.length; i++) {// O(N)
// heapInsert(arr, i);// O(logN)
// }
//做法2：
for (int i = arr.length-1; i >= 0 ; i--) {
heapify(arr, i, arr.length);
}
int size = arr.length;
//0位置上的数与heapsize最后一个数交换
swap(arr, 0, --size);
while (size > 0) {// O(N)
//0位置上的数重新调整位置
heapify(arr, 0, size);// O(logN)
//0位置上的数与heapsize最后一个数交换,heapsize减小
swap(arr, 0, --size);// O(1)
}
}
拓展题目
因为0位置上的正确数一定在0-6这七个数中，所以将这7个数在小根堆中排好序，最小值就可以弹出放到0位置上，然后再加入下一个数，进行重复操作。复杂度为 O ( N log k )
public void sortedArrDistanceLessK(int[] arr, int k) {
PriorityQueue<Integer> heap = new PriorityQueue<>();
int index = 0;
//k个数形成小根堆
for (; index < Math.min(arr.length, k); index++) {
heap.add(arr[index]);
}
int i = 0;
for (; index < arr.length; i++, index++) {
heap.add(arr[index]);//加一个数
arr[i] = heap.poll();//弹出一个最小值
}
while (!heap.isEmpty()) {//依次弹出k个最小值
arr[i++] = heap.poll();
}
}
小根堆会遇到不够空间时扩容，扩容就会复制一次，长度为多少，复杂度就为多少，一共扩容 logN 次，总扩容复杂度为 O ( N log N )，均摊下来每个元素，复杂度为 O ( log N ) 。
系统提供的堆，只能给一个数，弹出一个数，不能做到上述的高效操作，要实现有高效操作的，必须自己写。
桶排序
先按个位数放进桶，然后从左往右，先进先出导出，再按十位数排序，重复，再按百位
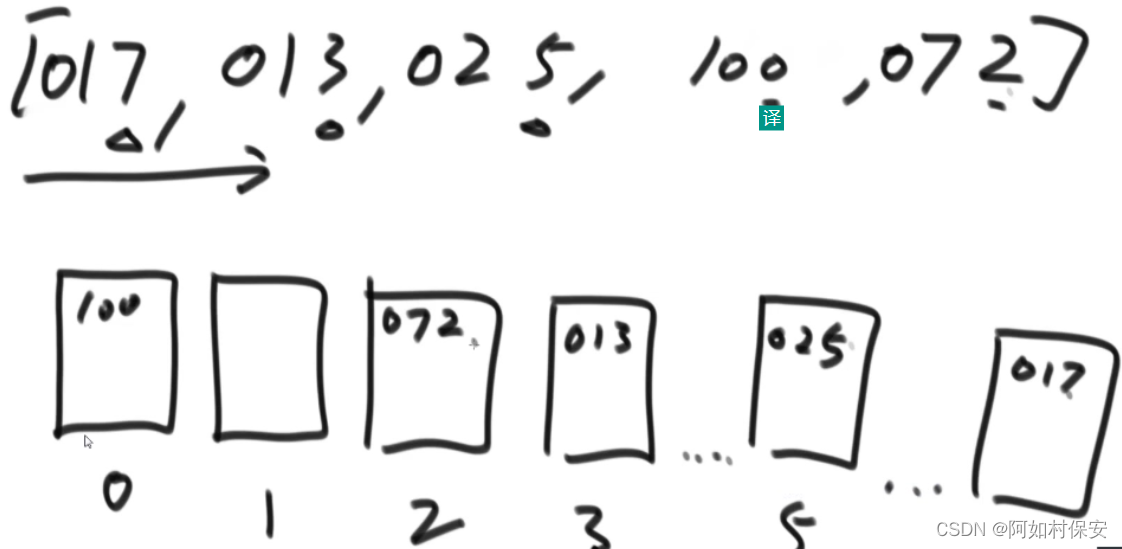
// only for no-negative value
public static void radixSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
radixSort(arr, 0, arr.length - 1, maxbits(arr));
}
//计算最大的十进制位是第几位
public static int maxbits(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);//寻找数组中最大的数
}
int res = 0;
while (max != 0) {
res++;
max /= 10;//自动整除，因为max是int
}
return res;
}
public static void radixSort(int[] arr, int begin, int end, int digit) {
final int radix = 10;
int i = 0, j = 0;
int[] bucket = new int[end - begin + 1];
//digit多少哥十进制位，也代表入桶出桶的次数
for (int d = 1; d <= digit; d++) {
int[] count = new int[radix];
//用于记录当前位上等于0,...,等于9的各有多少个数
for (i = begin; i <= end; i++) {
j = getDigit(arr[i], d);//确认当位上的数是多少
count[j]++;//等于该位上的数，统计加1
}
//用于记录当前位上小于等于0,...,小于等于9的各有多少个数
//同时也记录了当前位上等于0,...,等于9的数组最后一个数出桶后的位置
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
for (i = end; i >= begin; i--) {
j = getDigit(arr[i], d);
bucket[count[j] - 1] = arr[i];//出桶后的位置上放该数
count[j]--;//该桶上的数减一
}
for (i = begin, j = 0; i <= end; i++, j++) {
//把bucket的数组导入arr中，相当于保留了这次桶排序
arr[i] = bucket[j];
}
}
}
比较器
改写比较器
二、排序总结
稳定性
面试常见的坑
工程上的改进
在快速排序中，当样本量小于60的时候，插入排序时间复杂度相当，当常数操作复杂度极低，因此可以将2种混合起来。
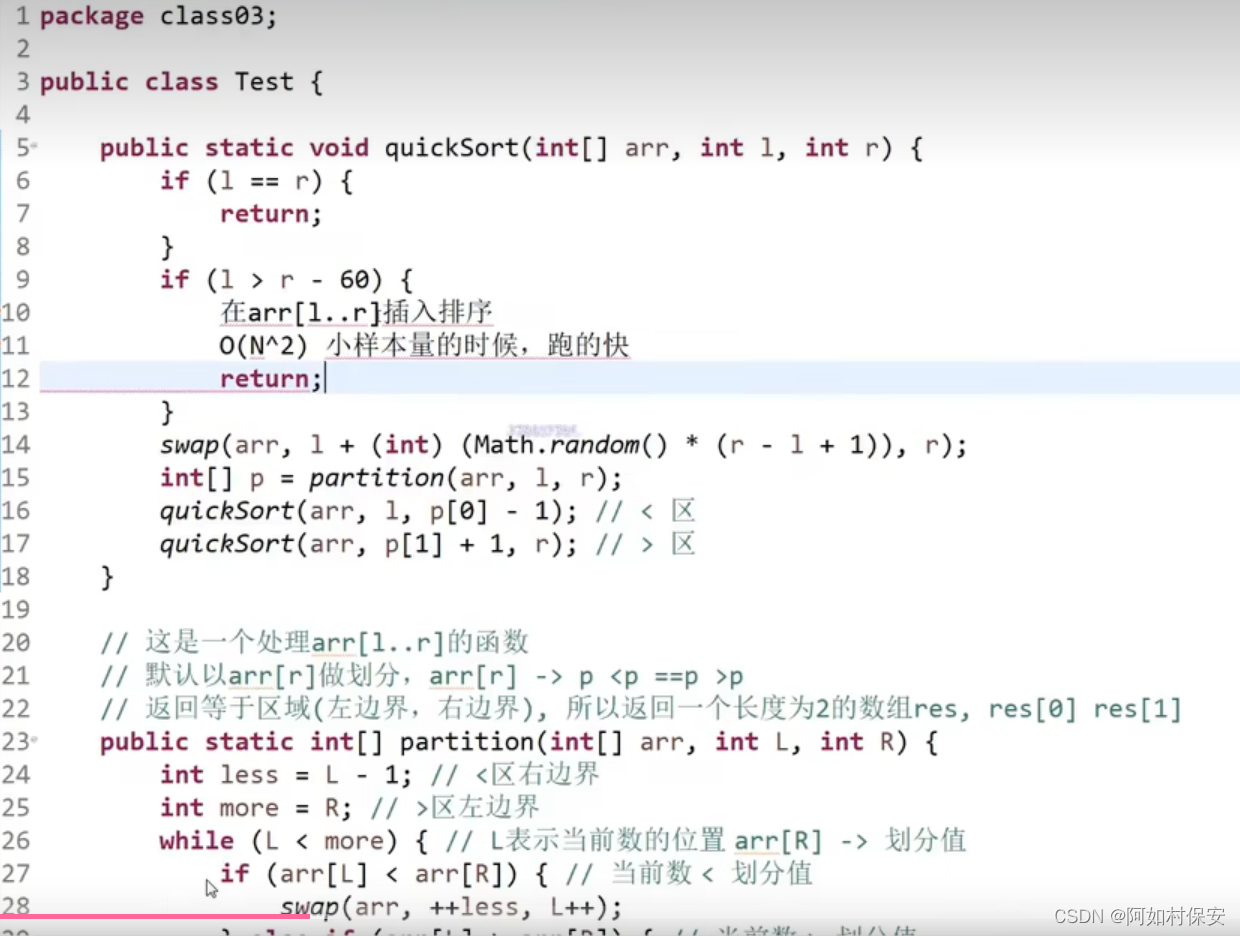
面试中会问到Arrays.sort()，如果比较基础类型的，就会使用快排，非基础类型用归并排序；因为快排没有稳定性，但是非基础类型不知道需不需要稳定性，因此非基础的用归并。
总结
其实，可以研究一下快排和插入排序的结合。
魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。
更多推荐
12
0- 0
已为社区贡献3条内容
所有评论(0)