---

线性表(Linear List)

• 定义：线性表是具有相同特性的数据元素的一个有限序列。由n(n≥0)个数据元素(结点)a1, a2, …，组成的有限序列。
  其中数据元素的个数n定义为表的长度； 当n=0时称为空表； 将非空的线性表(n>0)记作: (a1, a2, …an）；
  这里的数据元素ai(1≤i≤n)只是一个抽象的符号，其具体含义在不同的情况下可以不同。
  同一线性表中的元素必定具有相同特性，数据元素间的关系是线性关系。

• 特性：在非空的线性表，有且仅有一个开始结点a1，它没有直接前趋，而仅有一个直接后继a2;
  有且仅有一个终端结点an，它没有直接后继，而仅有一个直接前趋a_n-1；
  其余的内部结点ai(2≤i≤n-1)都有且仅有一个直接前趋a_i-1和一个直接后继a_i+1。
  线性表是一种典型的线性结构。

• 顺序存储结构存在问题：
  ① 存储空间分配不灵活
  ② 运算的空间复杂度高
  因此，推出链式存储结构。

线性表基本操作

基本操作(一)

InitList(&L)  //Initialization List

操作结果：初始化操作，构造一 个空的线性表L。

DestroyList(&L)

初始条件：线性表L已经存在。
操作结果：销毁已存在的线性表L。

ClearList(&L)

初始条件：线性表L已经存在。
操作结果：将线性表|重置为空表。

基本操作(二)

ListEmpty(L)

初始条件：线性表L已经存在。
操作结果：若线性表L为空表，则返回true；否则返回false。

ListLength(L)

初始条件：线性表L已经存在。
操作结果：返回线性表L中的数据元素个数。

基本操作(三)

GetElem(L,I,&e);

初始条件:线性表L已经存在，1<=i<= ListLength(L)。
操作结果:用e返回线性表L中第i个数据元素的值。

LocateElem(L,e,compare())

初始条件:线性表L已经存在，compare()是数据元素判定函数。
操作结果:返回L中第1个与e满足compare()的数据元素的位序。若这样的数据元素不存在则返回值为0。

基本操作(四)

PriorElem(L, cur_e, &pre_e)

初始条件：线性表L已经存在。
操作结果：若cur_e是L的数据元素，且不是第一个，则用pre_ e返回它的前驱，否则操作失败； pre_ e无意义。

NextElem(L, cur_ e, &next e)

初始条件：线性表L已经存在。
操作结果：若cur_e是L的数据元素，且不是第最后个，则用next_e返回它的后继，否则操作失败，next_ e无意义。

基本操作(五)

ListInsert(&L, i, e)

初始条件：线性表L已经存在，(1<=i<=ListLength(L)+1。
操作结果：在L的第i个位置之前插入新的数据元素e, L的长度加一。

基本操作(六)

ListDelete(&L,i,&e)

初始条件：线性表L已经存在，1< =i<=ListLength(L)。
操作结果：删除L的第i个数据元素,并用e返回其值，L的长度减一。

ListTraverse(&L, visited())

初始条件：线性表L已经存在。
操作结果：依次对线性表中每个元素调用visited()。

线性表存储结构

在计算机内，线性表有两种基本的存储结构：顺序存储结构和链式存储结构。

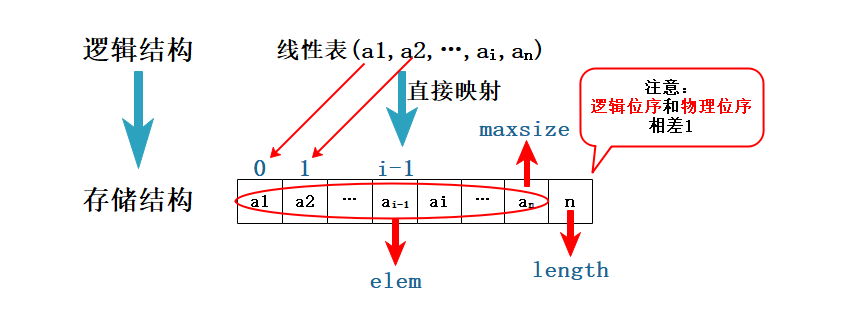
• 线性表的顺序存储表示：线性表的顺序表示又称为顺序存储结构或顺序映像。
• 顺序存储定义：把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。
• 基地址：线性表的第1个数据元素a1的存储位置，称作线性表的起始位置或基地址。

逻辑上相邻的，物理上也相邻。

#define list_init_size 100  //线性表存储空间的初始分配量
typedef struct{  //定义一个结构
	ElemType elem[list_init_size];
	int length;  //当前长度
}SqList;  //顺序表类型

typedef char ElemType;  //将ElemType定义成char，ElemType=char

静态分配内存
#define maxsize 100
typedef struct{
	ElemType elem[maxsize];
	int length;
}SqList;

动态分配内存
#define maxsize 100
typedef struct{
	ElemType *elem;
	int length;
}SqList;

L.elem=(ElemType*)malloc(sizeof(ElemType)*maxsize);

#define maxsize 10000  //图书表可能达到的最大长度
typedef strcut{  //图书信息定义
	char no[20];  //图书编号
	char name[50];  //图书名字
	float price;  //图书价格
}Book;
typedef struct{
	Book *elem;  //存储空间的基地址
	int length;  //图书表中当前图书个数
}SqList;  //图书表的顺序存储结构类型为SqList

顺序表（Sequence List）

线性表的顺序存储表示

• 定义：线性表的顺序存储结构。

• 顺序表(线性表的顺序存储结构)的特点：
  (1)利用数据元素的存储位置表示线性表中相邻数据元素之间的前后关系，顺序表的逻辑结构与存储结构总是一致的。
  (2)在访问线性表时，可以快速地计算出任何一个数据元素的存储地址。因此可以粗略地认为，访问每个元素所花时间相等。这种存取元素的方法被称为随机存取法。

• 顺序表优缺点：
  优点：
  ① 存储密度大(结点本身所占存储量/结点结构所占存储量)；
  ② 可以随机存取表中任一元素。
  缺点:
  ①在插入、删除某一元素时，需要移动大量元素；
  ② 浪费存储空间；
  ③ 属于静态存储形式，数据元素的个数不能自由扩充。

• 说明：
  在线性表中的序号为i，而在顺序表对应的数组elem中的下标为i-1。
  顺序表中的第一个元素下标为0，最后一个元素下标为数组长度。

顺序表基本操作的实现

（参数用引用）

算法解释：

#define maxsize 100
typrdef struct{
	ElemType *elem;
	int length;
}SqList;  //定义顺序表类型

就如：
int a;  //定义变量a，a是int型
SqList L;  //定义变量L，L是SqList这种类型的，L是个顺序表

线性表L的初始化：

Status InitList_Sq(SqList &L){  //构造一个空的顺序表L
	L.elem=new ElemType[maxsize];  //为顺序表分配空间
	if(!L.elem)  
		exit(overflow);  //存储分配失败
	L.length=0;  //空表长度为0
	return ok;
}

线性表L的销毁：

void DestroyList(SqList &L){
	if(L.elem)
		delete L.elem;  //释放存储空间
}

线性表L的清空：

void ClearList(SqList &L){
	L.length=0;  //将线性表的长度置为0
}

求线性表L的长度：

int GetLength(SqList L){
	return(L.length);
}

判断线性表L是否为空：

int IsEmpty(SqList L){
	if(L.length==0)
		return 1;
	else
		return 0;
}

顺序表L的取值：
（根据位置i获取相应位置数据元素的内容）

int GetElem(SqLis L,int i,ElemType &e){
	if(i<1||i>L.length)  //判断i值是否合理，若不合理，返回error
		return error;
	e=L.elem[i-1];  //第i-1的单位存储着第i个数据
	return ok;
}

顺序表L的查找：
【算法思路】
在线性表L中查找与指定值e相同的数据元素的位置；
从表的一端开始，逐个进行记录的关键字和给定值的比较。找到，返回该元素的位置序号，未找到，返回0。

int LocateElem(SqList L,ElemType e){
//在线性表L中查找值为e的数据元素，返回其序号（是第几个元素）
	for(i=0;i<length;i++)
		if(L.elem[i]==e)
			return i+1;  //查找成功，返回序号
	return 0;  //查找失败，返回0
}
或
int LocateElem(SqList L,ElemType e){
//在线性表L中查找值为e的数据元素，返回其序号（是第几个元素）
	while(i<L.length&&L.elem[i]!=e)
		i++;
		if(L.elem[i]==e)
			return i+1;  //查找成功，返回序号
	return 0;  //查找失败，返回0
}

时间复杂度：T(n)=O(n)
空间复杂度：S(n)=O(1)

顺序表L的插入：
线性表的插入运算是指在表的第i (1≤i≤n+1)个位置上，插入一个新结点e，使长度为n的线性表(a1,…,ai-1,ai,…,an)变成长度为n+1的线性表(a1,…,ai -1,e,ai,…,an)
【算法思想】
① 判断插入位置i是否合法。
② 判断顺序表的存储空间是否已满，若已满返回ERROR。
③ 将第n至第i位的元素依次向后移动一个位置，空出第i个位置。
④ 将要插入的新元素e放入第i个位置。
⑤ 表长加1，插入成功返回OK。

Status ListInsert_Sq(SqList &L,int i,ElemType e){
	if(i<1||i>L.length+1)  //i值不合法
		return error;
		if(L.lengt==maxsize)  //当前存储空间已满
			return error;
			for(j=L.length-1;j>=i-1;i--)
				L.elem[j+1]=L.elem[j];  //插入位置及之后的元素后移
			L.elem[i-1]=e;  //将新元素e放入第i个位置
			L.length++;  //表长+1
			return ok;
}

时间复杂度：T(n)=O(n)
空间复杂度：S(n)=O(1)

顺序表删除：
线性表的删除运算是指将表的第i(1≤i≤n)个结点删除使长度为n的线性表(a1,…,ai-1,ai,ai+1,…,an)变成长度为n-1的线性表(a1,…,ai-1,ai+1,…,an)
【算法思想】
①判断删除位置i是否合法(合法值为1≤i≤n)。
②将欲删除的元素保留在e中。
③将第i+1至第n位的元素依次向前移动一个位置。
④表长减1，删除成功返回OK。

Status ListDelete_Sq(SqList &L,int i){
	if((i<1)||(i>L.length))
		return error;  //值不合法
		for(j=i;j<=Length-1;j++)
			L.elem[j-1]=L.elem[j];  //被删除元素之后的元素前移
		L.length--;  //表长-1
		return ok;
}

时间复杂度：T(n)=O(n)
空间复杂度：S(n)=O(1)

---

ending~~~

有什么问题欢迎留言噢