【数据结构与算法/图论】Prim和Kruskal最小生成树算法正确性的证明
文章目录一、最小生成树简介二、最小生成树的性质一、最小生成树简介一个有nnn个顶点的连通图GGG的生成树是包含GGG中全部顶点的一个极小连通子图,它有且仅有n−1n-1n−1条边。也就是说,如果添加一条边,则构成回路;如果删去任何一条边,则生成树不再连通。一个生成树的代价为该生成树中所有边权的总和。称代价最小的生成树为最小生成树(Minimum Spanning Tree, MST)。最小生成树是
一、最小生成树简介
一个有 n n n个顶点的连通图 G = ( V , E ) G=(V,E) G=(V,E)的生成树是包含 G G G中全部顶点的一个极小连通子图,它有且仅有 n − 1 n-1 n−1条边。也就是说,如果添加一条边,则构成回路;如果删去任何一条边,则生成树不再连通。一个生成树的代价为该生成树中所有边权的总和。称代价最小的生成树为最小生成树(Minimum Spanning Tree, MST)。
最小生成树是图的一种重要应用,在城市道路交通规划、网络路由选择、城市通信网架设等实际问题中应用广泛。例如,在 n n n个城市之间架设通信网路,最多可设置 n ( n − 1 ) 2 n(n-1)\over2 2n(n−1)条线路,每条线路都有一定的成本,如何从这 n ( n − 1 ) 2 n(n-1)\over2 2n(n−1)条线路中选择 n − 1 n-1 n−1条线路,使得总成本最小?将这一问题表示为带权连通图,用图中的顶点表示城市,边表示城市之间的通信线路,边的权值为设置该线路所需的成本,则问题就可以转化为求这个图的最小生成树。
二、最小生成树的性质
定理1 最小生成树的子树也是最小生成树。
证明:设 T = ( V , E T ) T=(V,E_T) T=(V,ET)是图 G G G的一棵最小生成树, T ′ = ( U , E U ) ⊆ T T'=(U,E_U)\subseteq T T′=(U,EU)⊆T,下面证明 T ′ T' T′是 U U U的导出子图 G ′ G' G′的最小生成树。若 T ′ T' T′不是 G ′ G' G′的最小生成树,则取 G ′ G' G′的最小生成树 T ∗ T^* T∗,用 T ∗ T^* T∗中的边替换 T T T在 U U U中的边 E U E_U EU可以得到代价更小的生成树,这与 T T T是最小生成树矛盾。因此 T ′ T' T′一定是 G ′ G' G′的最小生成树。∎
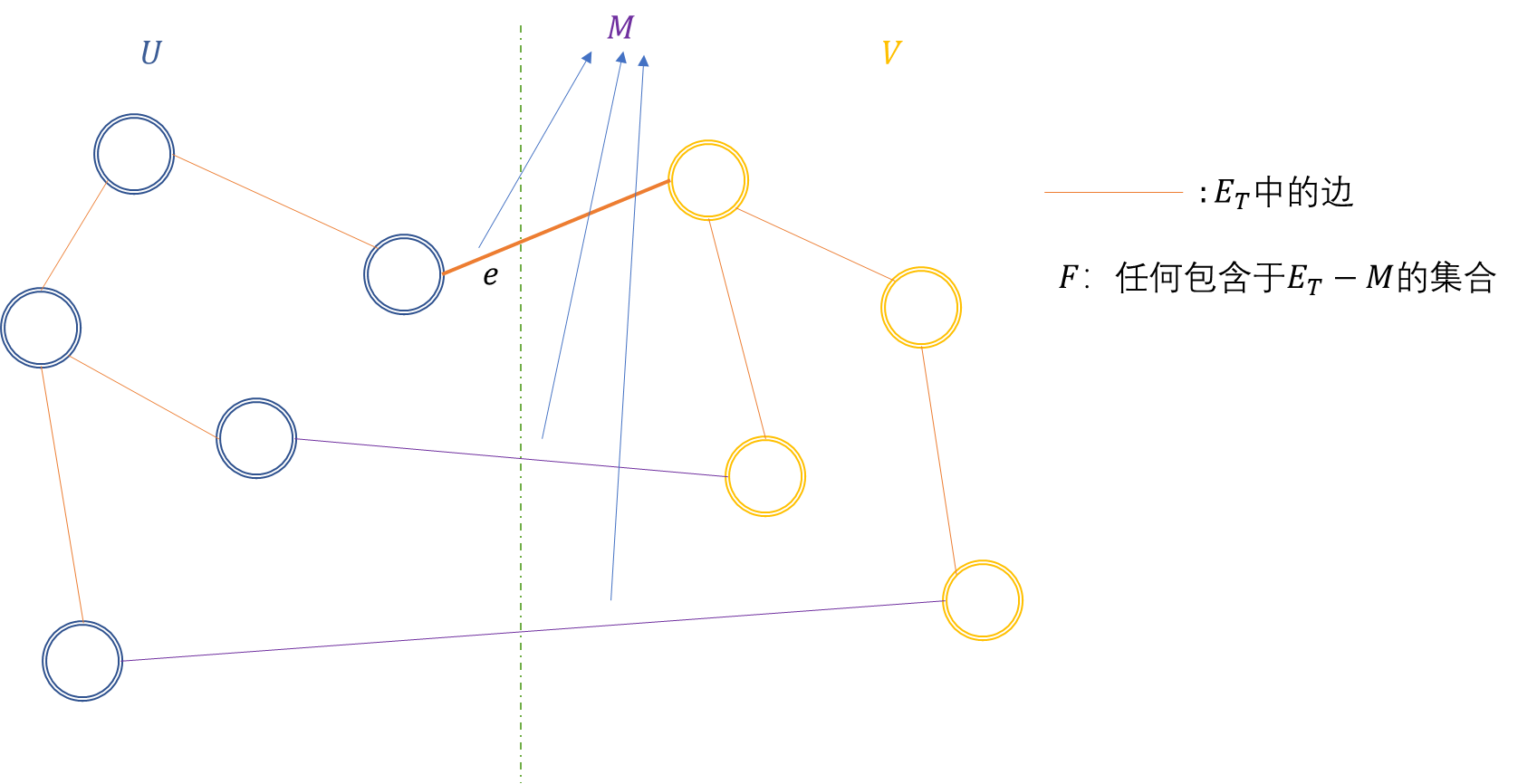
定理2(Key Property) 设 T = ( V , E T ) T=(V,E_T) T=(V,ET)是图 G = ( V , E ) G=(V,E) G=(V,E)的一棵最小生成树, w ( e ) w(e) w(e)表示边 e e e的权值。假设 F ⊆ E T F\subseteq E_T F⊆ET(即 F F F是 T T T的边集的子集), U ⊂ V U\subset V U⊂V是 G G G的一个点集,边集 M = { ( u , v ) ∈ E ∣ u ∈ U , v ∈ V − U } M=\{(u,v)\in E|u\in U,v\in V-U\} M={(u,v)∈E∣u∈U,v∈V−U}是所有连接 U U U和 V − U V-U V−U的边的集合,且 F ∩ M = ∅ F\cap M=\emptyset F∩M=∅。设 e e e是 M M M中权值最小的边,则 F ∪ { e } F\cup\{e\} F∪{e}是某个最小生成树 T ′ T' T′(可能不等于 T T T)的边集的子集。
证明:若 e ∈ T e\in T e∈T,则无需证明。所以我们假设 e ∉ T e\notin T e∈/T。
将 e e e加入 T T T的边集 E T E_T ET中,必形成回路。取 e ′ ∈ E T ∩ M e'\in E_T\cap M e′∈ET∩M(即 e ′ e' e′是 T T T中连接 U U U和 V − U V-U V−U的桥梁),则有 w ( e ) ≤ w ( e ′ ) w(e)\le w(e') w(e)≤w(e′)。令 T ′ = ( V , ( E T − { e ′ } ) ∪ { e } ) T'=(V,(E_T-\{e'\})\cup\{e\}) T′=(V,(ET−{e′})∪{e}),则 T ′ T' T′的代价不高于 T T T,所以 T ′ T' T′是一棵最小生成树。∎
三、Prim算法
设 G = ( V , E ) G=(V,E) G=(V,E)为带权连通图,要在 G G G中构造一棵最小生成树 T = ( U , E T ) T=(U,E_T) T=(U,ET)。Prim算法的基本思想如下:
(1) 初始化顶点集 U = { u 0 } U=\{u_0\} U={u0},其中 u 0 ∈ V u_0\in V u0∈V是 U U U中唯一的元素;令 E T = ∅ E_T=\emptyset ET=∅,即一开始树中没有边。
(2) 在所有满足 u ∈ U u\in U u∈U、 v ∈ V − U v\in V-U v∈V−U的边 ( u , v ) ∈ E (u,v)\in E (u,v)∈E中选择一条权值最小的边 e = ( u ∗ , v ∗ ) e=(u^*,v^*) e=(u∗,v∗)加入最小生成树的边集 E T E_T ET中,同时将顶点 v ∗ v^* v∗并入 U U U中。
重复以上过程,直到 U = V U=V U=V为止。此时 ∣ E T ∣ = n − 1 |E_T|=n-1 ∣ET∣=n−1, T T T是 G G G的一棵最小生成树。
因为每次操作是将一个节点并入 U U U中,所以Prim算法也称扩点法。
正确性证明:
归纳假设:每一步得到的树 T U = ( U , E U ) T_U=(U,E_U) TU=(U,EU)是都是某棵最小生成树的子树。
① 归纳基础:初始条件 T { u 0 } = ( { u 0 } , ∅ ) T_{\{u_0\}}=(\{u_0\},\emptyset) T{u0}=({u0},∅)是所有最小生成树的子树(因为空集是所有集合的子集)。
② 归纳步:设我们已经得到 T U = ( U , E U ) T_U=(U,E_U) TU=(U,EU)是最小生成树 T T T的子树。按规则选取边 e = ( u ∗ , v ∗ ) e=(u^*,v^*) e=(u∗,v∗)。根据定理2, E U ∪ { e } E_U\cup\{e\} EU∪{e}是某棵最小生成树 T ′ T' T′的边集的子集。因此该步得到的树 T U ∪ { v ∗ } = ( U ∪ { v ∗ } , E U ∪ { e } ) T_{U\cup\{v^*\}}=(U\cup\{v^*\},E_U\cup\{e\}) TU∪{v∗}=(U∪{v∗},EU∪{e})是 T ′ T' T′的最小生成树。
③ 终止:最后 U = V U=V U=V时, T V = ( V , E V ) T_V=(V,E_V) TV=(V,EV)是某棵最小生成树的子树,而这棵最小生成树就是 T V T_V TV本身,因此我们求得了 G G G的一棵最小生成树。∎
代码实现:
(1) 不加优化的暴力解法
暴力选取边 e = ( u ∗ , v ∗ ) e=(u^*,v^*) e=(u∗,v∗)。时间复杂度 O ( n m ) O(nm) O(nm)。
int Prim()
{
in[1] = true; // u0
int ans = 0;
for(int i = 1; i < n; ++i)
{
int min_val = 1e9, min_e = -1;
for(int u = 1; u <= n; ++u)
{
if(!in[u]) continue;
for(int e = first[u]; e; e = nxt[e])
{
int v = go[e];
if(in[v]) continue;
if(val[e] < min_val)
{
min_val = val[e];
min_e = e;
}
}
}
in[go[min_e]] = true;
ans += min_val;
}
return ans;
}
(2) 堆优化的Prim算法
用堆来优化选取权值最小的边 e = ( u ∗ , v ∗ ) e=(u^*,v^*) e=(u∗,v∗)的过程。我们定义vis数组表示节点是否属于集合 U U U,dis数组表示 V − U V-U V−U中的节点到 U U U的最短边。每当我们向 U U U中加入一个节点,就将它的vis标记为true,并更新它所连接的节点的dis值,若dis值被更新就将这条边加入堆中。从堆中取出最小值时,有可能边的两个端点都在 U U U中了,所以要检查端点的vis值。注意,堆中存储的边不是集合 M = { ( u , v ) ∈ E ∣ u ∈ U , v ∈ V − U } M=\{(u,v)\in E|u\in U,v\in V-U\} M={(u,v)∈E∣u∈U,v∈V−U},有两点区别:
① 堆中可能会有两端点都属于 U U U的边;
② 当dis值没有被更新时,该边不会入队,从而降低了时间复杂度。
时间复杂度:下面的代码复杂度高达 O ( m log m ) O(m\log m) O(mlogm),因为同一个v可能在Q里出现多次,导致堆中元素数量在 O ( m ) O(m) O(m)级别。但堆优化的Prim算法复杂度理论上是 O ( m log n ) O(m\log n) O(mlogn)的,在 Q Q Q里进行的操作是Decrease Key,即改变某个节点对应的dis值,这样每个节点只会在堆中出现一次。
int dis[MAXN];
bool vis[MAXN];
int Prim()
{
int ans = 0;
memset(dis, 0x3f, sizeof(dis));
priority_queue<node> Q;
Q.push({1, 0});
for(int cnt = 1; cnt <= n;)
{
node nd = Q.top();
Q.pop();
int u = nd.u;
if(vis[u]) continue;
vis[u] = true;
ans += nd.d;
++cnt;
for(int e = first[u]; e; e = nxt[e])
{
int v = go[e];
if(dis[v] > val[e])
{
dis[v] = val[e];
Q.push({v, val[e]});
}
}
}
return ans;
}
四、Kruskal算法
Kruskal算法的基本思想如下:
(1) 初始状态为 T = ( V , ∅ ) T=(V,\emptyset) T=(V,∅),即开始时最小生成树 T T T中只包含了所有的顶点,而没有边,此时 T T T中有 n n n个连通分量。
(2) 将 E E E中的边按权值递增的顺序排列,并按照这一顺序一次尝试将边加入最小生成树 T T T中:如果这条边的端点分别位于 T T T的不同的连通分量中,则将该边加入 T T T;否则舍弃该边(为了保证不出现环)。
依此类推,直到 T T T中有 n − 1 n-1 n−1条边为止,此时 T T T中只有一个连通分量。
正确性证明:
考虑加入边 e = ( u , v ) e=(u,v) e=(u,v)的操作。假设已经被算法选定的边集为 E U E_U EU,令 E U E_U EU中所有边关联的所有顶点的集合为 U U U。显然, U U U和 V − U V-U V−U是不连通的。根据定理2,我们只需证明 e e e是连接集合 U U U和 V − U V-U V−U的权值最小的边,就能推出最后得到的树是最小生成树。
假设还有比 e e e权值更小的连接集合 U U U和 V − U V-U V−U的边 e ′ e' e′,则根据算法的步骤, e ′ e' e′一定会在 e e e之前被算法考虑。因为此时 U U U和 V − U V-U V−U一定不连通(否则后面考虑 e e e的时候 U U U和 V − U V-U V−U就连通了),所以 e ′ e' e′一定会被选择。但加入边 e ′ e' e′后会导致 U U U和 V − U V-U V−U连通,与已知条件矛盾。所以假设不成立,我们证明了 e e e是连接集合 U U U和 V − U V-U V−U的权值最小的边。∎
代码实现:
边按权值排序+并查集。时间复杂度 O ( m log m ) O(m\log m) O(mlogm)。
struct edge
{
int u, v, w;
bool operator<(const edge& o) const
{
return w < o.w;
}
} e[MAXM];
int fa[MAXN]; // 并查集
int getfa(int x)
{
return x == fa[x] ? x : fa[x] = getfa(fa[x]);
}
int Kruskal()
{
sort(e + 1, e + m + 1); // 按边权排序
for(int i = 1; i <= n; ++i) fa[i] = i;
int k = 0, ans = 0;
for(int i = 1; i <= m && k < n; ++i)
{
int x = getfa(e[i].u);
int y = getfa(e[i].v);
if(x != y)
{
++k;
ans += e[i].w;
fa[x] = y;
}
}
return ans;
}
参考文献

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)