【数据结构】B树和B+树（定义查找删除插入）解析+完整代码

5叉查找树查找方式：顺序查找每个灰框里的元素，找不到则去孩子那里找。如何保证查找效率？若每个结点内关键字太少，导致树变高，要查更多层结点，效率低。解决策略：1.m叉树中，规定除了根节点外，任何结点至少有⌈m2⌉⌈m/2⌉，即至少含有⌈m2⌉−1⌈m/2⌉−1个关键词。2.m叉查找树中，规定对于任何结点，其所有子树的高度都要相同。B树定义B树，又称多路平衡查找树，B树中被允许的孩子个数的最大值称为B

YY_D_S_

1278人浏览 · 2024-05-20 11:50:49

YY_D_S_ · 2024-05-20 11:50:49 发布

4.B树和B+树

4.1 B树

4.1.1 定义

5叉查找树
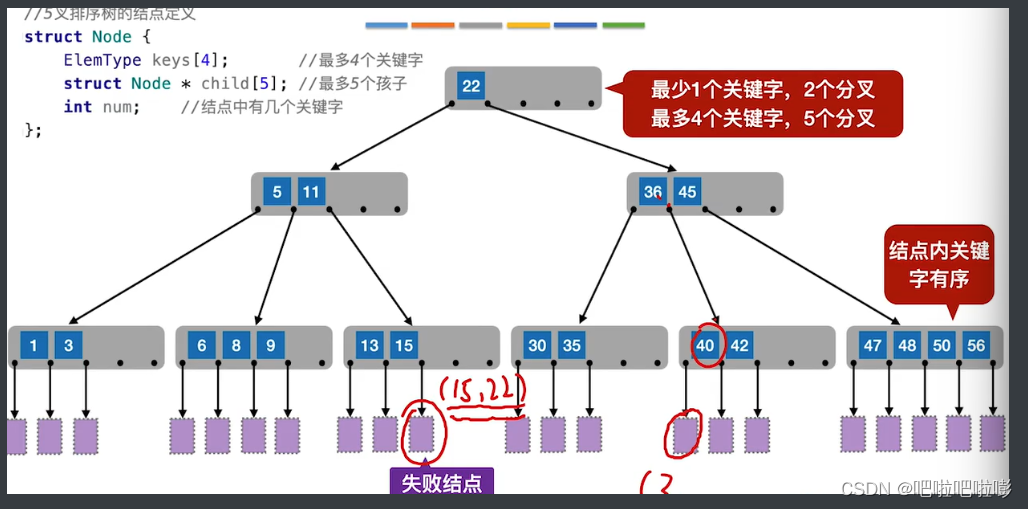
- 查找方式：顺序查找每个灰框里的元素，找不到则去孩子那里找。
- 如何保证查找效率？
若每个结点内关键字太少，导致树变高，要查更多层结点，效率低。

解决策略：

1.m叉树中，规定除了根节点外，任何结点至少有 $⌈m/2⌉\lceil m/2 \rceil$ ，即至少含有 $⌈m/2⌉−1\lceil m/2 \rceil -1$ 个关键词。

2.m叉查找树中，规定对于任何结点，其所有子树的高度都要相同。
B树定义
B树，又称多路平衡查找树，B树中被允许的孩子个数的最大值称为B树的阶，通常用m表示。

一棵m阶B树满足以下特性：

1.树中每个结点至多有m棵子树，即至多含有m-1个关键字；

2.若根结点不是终端结点，则至少有两棵子树（即一个关键字）；

3.除根结点外的所有非叶子结点至少有$\lceil m/2 \rceil $棵子树，即至少含有$ \lceil m/2 \rceil-1$个关键字；

4.所有的叶结点都出现在同一层次上，并且不带信息（可以视为外部结点或类似于折半查找判定树的查找失败结点，实际上这些节点不存在，指向这些结点的指针为空）。
- 所谓m阶B树，是所有结点的平衡因子均为0的m路平衡查找树。B树的叶结点代表查找失败的情况。
B树的核心特性

1.根结点的子树数范围： $[2, m]$ ，关键字数范围： $[1, m - 1]$

其他结点的子树数范围： $[⌈m/2⌉],m][\lceil m/2 \rceil],m]$ ，关键字数范围： $[⌈m/2⌉−1,m−1][\lceil m/2 \rceil-1,m-1]$ 。

2.对任一结点，其所有子树高度都相同。

3.关键字的值：子树0<关键字1<子树1<关键字2<子树2……（类比二叉查找树左<中<右）
求B树的最小高度

让每个结点尽可能的满，即每个结点有有m-1个关键字，m

4.1.2 查找

步骤

1.在B树中找结点；（同二叉排序树的查找）

2.在结点中找关键字。（顺序或二分查找）

4.1.3 插入

方法
1.插入key后，若导致原结点关键字数超过上限，

2.则从中间位置（$\lceil m/2 \rceil $）将其中的关键字分为两部分，

（1）左部分包含的关键字放在原结点中，

（2）右部分包含的关键字放到新结点中，

（3）中间位置（ $⌈m/2⌉\lceil m/2 \rceil$ ）的结点插入原结点的父结点（若没有则新建）。

3.若此时导致其父结点的关键字个数也超过上限，则继续进行这种分裂操作，直至这个过程传到根结点为止，进而导致B树高度增加1.
- 注：新元素一定是插入到最底层终端节点，用查找来确定插入位置。
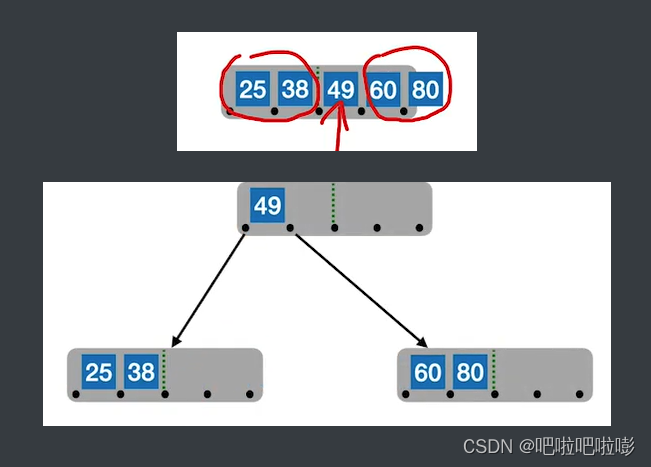
核心要求

1.对m阶B树——除根结点外，结点关键字个数 $⌈m/2⌉−1<=n<=m−1\lceil m/2 \rceil -1<=n<=m-1$ ；

2.子树0<关键字1<子树1<关键字2<子树2<……

4.1.4 删除

方法
- 若被删除关键字在终端结点，则直接删除该关键字（要注意结点关键字个数是否低于下限 $⌈m/2⌉−1\lceil m/2 \rceil -1$ ）。
- 若被删除关键字在非终端结点，则用直接前驱或直接后继来代替被删除的关键字。
  
  直接前驱：当前关键字左侧指针所指子树中最右下的元素。
  
  直接后继：当前关键字右侧指针所指子树中最左下的元素。
  
  对非终端结点关键字的删除，必然可以转化为对终端结点的删除操作。
- 如果删除后低于下限 $⌈m/2⌉−1\lceil m/2 \rceil -1$ ：
  
  1.兄弟够借
  
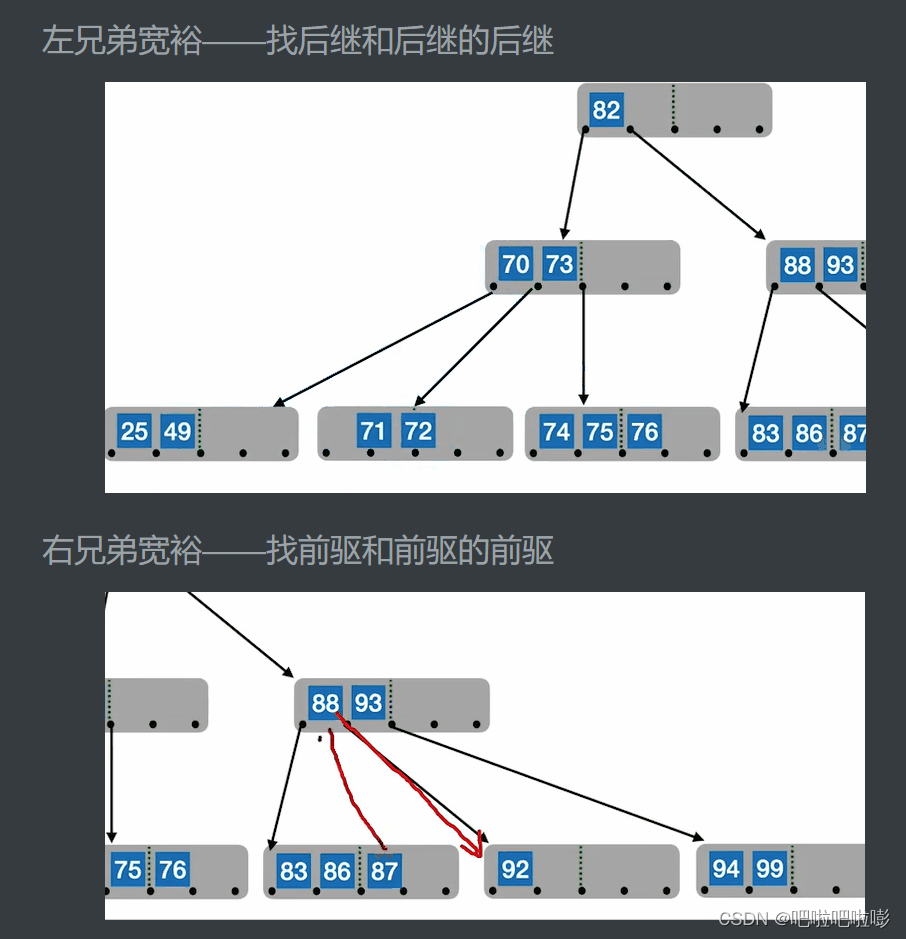
  若被删除关键字所在结点删除前的关键字个数低于下限，且与此结点右（或左）兄弟结点的关键字个数还很宽裕，则需要调整该结点、右（或左）兄弟结点及其双亲结点（父子换位法）。
  - 即当左兄弟宽裕时，用当前结点的后继、后继的后继来填补空缺。
    
    当右兄弟宽裕时，用当前结点的前驱、前驱的前驱来填补空缺。
  - 例：
    
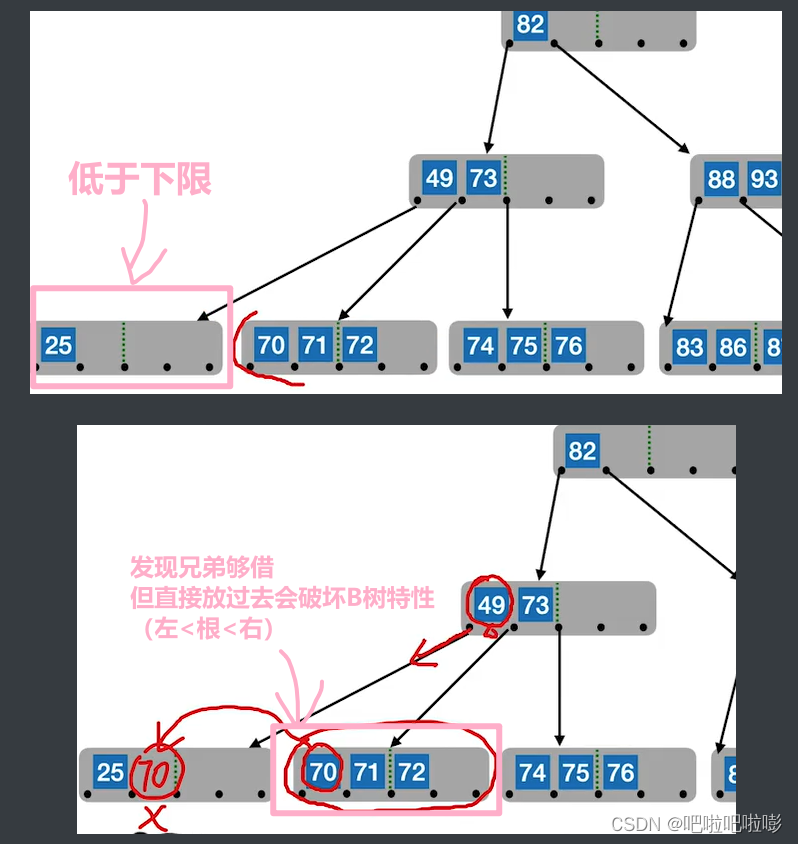
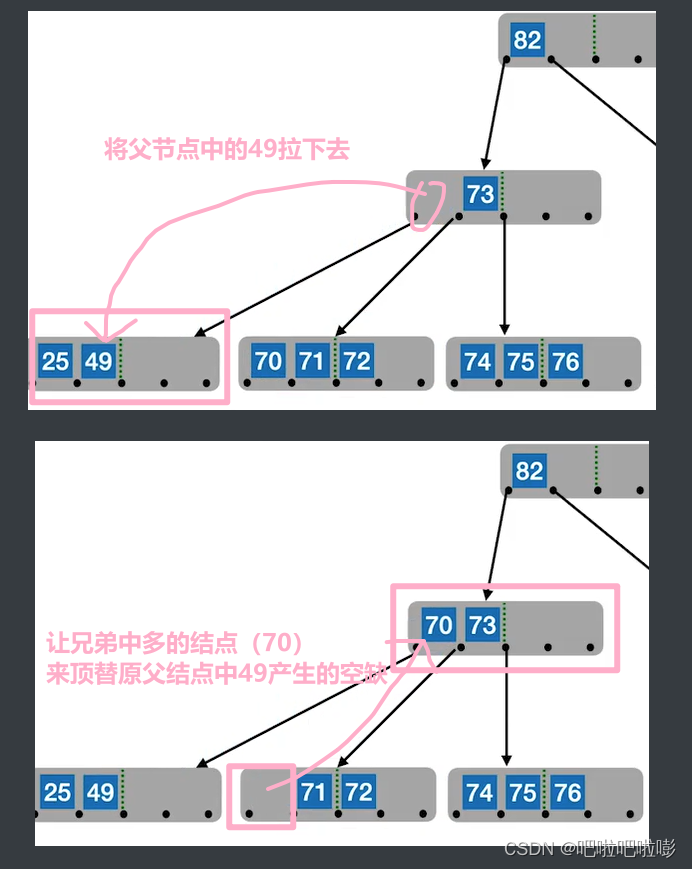
    即：
    
    左兄弟宽裕——找后继和后继的后继
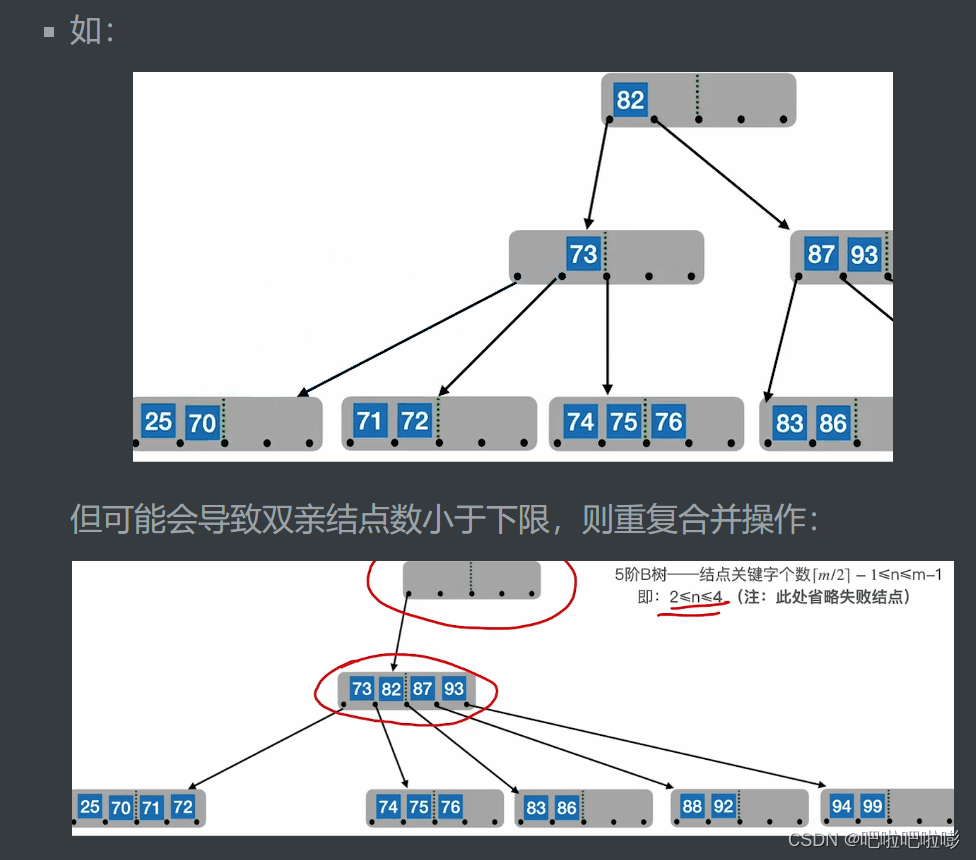
2.兄弟不够借

若被删除关键字所在结点删除前的关键字个数低于下限，且左右兄弟结点关键字个数均 $=⌈m/2⌉−1=\lceil m/2 \rceil-1$ ，

则将关键字删除后，与左（或右）兄弟结点及双亲结点中的关键字进行合并。

在合并过程中，双亲结点中关键字个数会减1。

若双亲结点是根结点且关键字个数减少为0，则直接将根结点删除，合并后的新结点为根；

若双亲结点不是根结点，且关键字个数低于下限，则又要与它自己的兄弟结点进行调整或合并操作，直到符合要求。
- 如：
删除操作总结

在这里插入图片描述

*完整代码 B树

#include <stdio.h>
#include <stdlib.h>

#define M 5 // B 树的阶数

typedef int ElemType; // 关键字的数据类型

// B 树的结点结构
typedef struct Node {
    ElemType keys[M - 1]; // 关键字数组
    struct Node *child[M]; // 子结点指针数组
    int num; // 结点中有几个关键字
} Node;

// 创建新结点
Node *createNode() {
    Node *newNode = (Node *)malloc(sizeof(Node)); // 分配新结点的内存空间
    newNode->num = 0; // 初始化结点中的关键字数量为0
    for (int i = 0; i < M; i++)
        newNode->child[i] = NULL; // 将子结点指针数组初始化为空
    return newNode; // 返回新创建的结点
}

// 在 B 树中查找关键字
Node *search(Node *root, ElemType key) {
    int i = 0;
    while (i < root->num && key > root->keys[i]) // 在当前结点中查找关键字的位置
        i++;
    if (i < root->num && key == root->keys[i]) // 如果找到关键字，则返回当前结点
        return root;
    if (root->child[i] == NULL) // 如果当前结点没有子结点，则关键字不存在
        return NULL;
    else
        return search(root->child[i], key); // 否则递归在子结点中查找关键字
}

// 分裂子结点
void splitChild(Node *parent, int index, Node *child) {
    Node *newChild = createNode(); // 创建新的子结点
    newChild->num = M / 2 - 1; // 新子结点中关键字数量为 M / 2 - 1
    for (int i = 0; i < M / 2 - 1; i++)
        newChild->keys[i] = child->keys[i + M / 2]; // 将原子结点的后半部分关键字复制到新子结点
    if (child->child[0] != NULL) {
        for (int i = 0; i < M / 2; i++)
            newChild->child[i] = child->child[i + M / 2]; // 如果子结点不是叶子结点，则将原子结点的后半部分子结点指针复制到新子结点
    }
    child->num = M / 2 - 1; // 更新原子结点中的关键字数量为 M / 2 - 1
    for (int i = parent->num; i > index; i--)
        parent->child[i + 1] = parent->child[i]; // 将父结点中的子结点指针数组向后移动一个位置
    parent->child[index + 1] = newChild; // 将新子结点插入到父结点的指定位置
    for (int i = parent->num - 1; i >= index; i--)
        parent->keys[i + 1] = parent->keys[i]; // 将父结点中的关键字数组向后移动一个位置
    parent->keys[index] = child->keys[M / 2 - 1]; // 将原子结点中的中间关键字提升到父结点中
    parent->num++; // 更新父结点中的关键字数量
}

// 插入关键字
void insertNonFull(Node *node, ElemType key) {
    int i = node->num - 1;
    if (node->child[0] == NULL) {
        while (i >= 0 && key < node->keys[i]) { // 在当前结点中找到关键字应插入的位置
            node->keys[i + 1] = node->keys[i]; // 将较大的关键字向后移动一个位置
            i--;
        }
        node->keys[i + 1] = key; // 将关键字插入到找到的位置
        node->num++; // 更新结点中的关键字数量
    } else {
        while (i >= 0 && key < node->keys[i])
            i--;
        i++;
        if (node->child[i]->num == M - 1) { // 如果子结点已满
            splitChild(node, i, node->child[i]); // 分裂子结点
            if (key > node->keys[i]) // 确定插入的位置
                i++;
        }
        insertNonFull(node->child[i], key); // 递归插入关键字到子结点
    }
}

// 插入操作
Node *insert(Node *root, ElemType key) {
    if (root == NULL) { // 如果根结点为空，创建新的根结点
        root = createNode();
        root->keys[0] = key;
        root->num = 1;
    } else {
        if (root->num == M - 1) { // 如果根结点已满
            Node *newRoot = createNode(); // 创建新的根结点
            newRoot->child[0] = root;
            splitChild(newRoot, 0, root); // 分裂根结点
            int i = 0;
            if (newRoot->keys[0] < key)
                i++;
            insertNonFull(newRoot->child[i], key); // 在新根结点中递归插入关键字
            root = newRoot; // 更新根结点
        } else {
            insertNonFull(root, key); // 根结点未满，直接插入关键字
        }
    }
    return root;
}

// 删除关键字
void removeFromNode(Node *node, ElemType key) {
    int i = 0;
    while (i < node->num && key > node->keys[i]) // 在当前结点中查找关键字的位置
        i++;
    if (i < node->num && key == node->keys[i]) { // 如果找到关键字
        if (node->child[0] == NULL) { // 如果是叶子结点，直接删除关键字
            for (int j = i; j < node->num - 1; j++)
                node->keys[j] = node->keys[j + 1]; // 将后面的关键字向前移动
            node->num--; // 更新结点中的关键字数量
        } else {
            Node *successor = node->child[i + 1]; // 如果不是叶子结点，找到关键字的后继
            while (successor->child[0] != NULL) // 后继为最左边的叶子结点
                successor = successor->child[0];
            node->keys[i] = successor->keys[0]; // 将后继的关键字替换当前关键字
            removeFromNode(successor, node->keys[i]); // 递归删除后继的关键字
        }
    } else { // 关键字在子结点中
        if (node->child[i] == NULL) { // 如果子结点为空，关键字不存在
            printf("关键字 %d 不存在\n", key);
            return;
        }
        removeFromNode(node->child[i], key); // 在子结点中递归删除关键字
    }
}

// 删除操作
Node *removeKey(Node *root, ElemType key) {
    if (root == NULL) { // 如果根结点为空，B 树为空
        printf("B 树为空\n");
        return NULL;
    }
    removeFromNode(root, key); // 在根结点中删除关键字
    // 如果根结点关键字数量为0，且根结点不是叶子结点，调整树的高度
    if (root->num == 0 && root->child[0] != NULL) {
        Node *newRoot = root->child[0];
        free(root); // 释放原根结点的内存
        root = newRoot; // 更新根结点
    }
    return root;
}

// 释放 B 树
void freeBTree(Node *root) {
    if (root) {
        for (int i = 0; i < root->num + 1; i++)
            freeBTree(root->child[i]); // 递归释放所有子结点的内存
        free(root); // 释放当前结点的内存
    }
}

// 打印 B 树（中序遍历）
void printBTree(Node *root) {
    if (root) {
        for (int i = 0; i < root->num; i++) {
            printBTree(root->child[i]); // 递归打印所有左子树
            printf("%d ", root->keys[i]); // 打印当前关键字
        }
        printBTree(root->child[root->num]); // 递归打印最右边的子树
    }
}

int main() {
    Node *root = NULL;

    // 插入操作测试
    root = insert(root, 10);
    root = insert(root, 20);
    root = insert(root, 5);
    root = insert(root, 6);
    root = insert(root, 12);
    root = insert(root, 30);
    root = insert(root, 7);
    root = insert(root, 17);
    root = insert(root, 21);
    root = insert(root, 25);

    printf("After insert B Tree:\n");
    printBTree(root);
    printf("\n");

    // 查询操作测试
    ElemType keyToFind = 12;
    Node *foundNode = search(root, keyToFind);
    if (foundNode)
        printf("Key %d in the B Tree\n", keyToFind);
    else
        printf("Key %d not in the B Tree\n", keyToFind);

    // 删除操作测试
    ElemType keyToRemove = 12;
    root = removeKey(root, keyToRemove);
    printf("The B tree after delete Key %d :\n", keyToRemove);
    printBTree(root);
    printf("\n");

    // 查询操作测试
    ElemType keyToFind2 = 12;
    Node *foundNode2 = search(root, keyToFind2);
    if (foundNode2)
        printf("Key %d in the B Tree\n", keyToFind2);
    else
        printf("Key %d not in the B Tree\n", keyToFind2);

    // 释放内存
    freeBTree(root);

    return 0;
}

4.2 B+树

定义

一棵m阶的B+树需满足下列条件：

（1）每个分支结点最多有m棵子树（孩子结点）。

（2）非叶根结点至少有两棵子树，

其他每个分支结点至少有 $⌈m/2⌉\lceil m/2 \rceil$ 棵子树。

（3）结点在子树个数与关键字个数相等。

（4）所有叶结点包含全部关键字及指向相应记录的指针，叶结点中将关键字大小顺序排列，并且相邻叶结点按大小顺序相互链接起来。

B和B+的区别

B树	B+树
n个关键字对应n+1棵子树。	n个关键字对应n个子树。
根结点的关键字树= $[1, m - 1]$ ；其他结点关键字数 $[⌈m/2⌉−1,m−1][\lceil m/2\rceil-1,m-1]$ 。	根结点的关键字树= $[1, m]$ ；其他结点关键字数 $[⌈m/2⌉,m][\lceil m/2\rceil,m]$ 。
各结点中包含的关键字不重复。	叶结点包含全部关键字，非叶结点中出现过的关键字也会出现在叶结点中。
结点中都包含了关键字对应的记录的存储地址。	叶子结点包含信息，所有非叶子结点仅起到索引作用，非叶子结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针，不含有该关键字对应记录的存储地址。

B+树优点

在B+树中，非叶结点不含有该关键字对应记录的存储地址。

可以使一个磁盘块可以包含更多个关键字，使B+树的阶更大，树高更矮，读磁盘次数更少，查找更快。

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。