数据结构树的基本操作_数据结构树的基本操作(主要遍历）

一．实验目的将树的基本操作C语言实现，主要考察树的先序，中序，后序和层次遍历。二.主要内容本文所使用的二叉树如图：显然先序：ABCDEGF中序：CBEGDFA后序：CGEFDBA层次：ABCDEFGBiTree.h内容C++typedef char TElemType;typedef int Status;typedef struct BiTNode{TElemType data;struct

胡安黄

773人浏览 · 2021-01-17 17:29:19

胡安黄 · 2021-01-17 17:29:19 发布

一．实验目的

将树的基本操作C语言实现，主要考察树的先序，中序，后序和层次遍历。

二.主要内容

本文所使用的二叉树如图：

显然

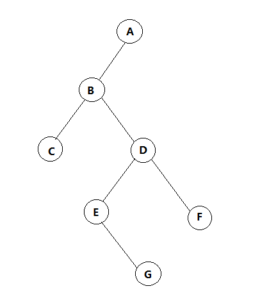
先序：ABCDEGF

中序：CBEGDFA

后序：CGEFDBA

层次：ABCDEFG

BiTree.h内容

C++

typedef char TElemType;

typedef int Status;

typedef struct BiTNode{

TElemType data;

struct BiTNode *lchild,*rchild;

}BiTNode,*BiTree;

Status PreCreateBiTree(BiTree &T);//先序输入二叉树

Status PreOrderTraverse(BiTree T,Status(*Visit)(TElemType e));

Status InOrderTraverse1(BiTree T,Status(*Visit)(TElemType e));

Status InOrderTraverse2(BiTree T,Status(*Visit)(TElemType e));

Status PostOrderTraverse(BiTree T,Status(*Visit)(TElemType e));

Status LevelOrderTraverse(BiTree T,Status(*Visit)(TElemType e));

Status Visit(TElemType e);

Status GetDepth(BiTree T);

Status CountNode(BiTree T,int &d);

typedefcharTElemType;

typedefintStatus;

typedefstructBiTNode{

TElemTypedata;

structBiTNode*lchild,*rchild;

}BiTNode,*BiTree;

StatusPreCreateBiTree(BiTree&T);//先序输入二叉树

StatusPreOrderTraverse(BiTreeT,Status(*Visit)(TElemTypee));

StatusInOrderTraverse1(BiTreeT,Status(*Visit)(TElemTypee));

StatusInOrderTraverse2(BiTreeT,Status(*Visit)(TElemTypee));

StatusPostOrderTraverse(BiTreeT,Status(*Visit)(TElemTypee));

StatusLevelOrderTraverse(BiTreeT,Status(*Visit)(TElemTypee));

StatusVisit(TElemTypee);

StatusGetDepth(BiTreeT);

StatusCountNode(BiTreeT,int&d);

主要函数：

① 先序创建二叉树

注意创建的时候如果没有左右子树要输入空格

输入：ABC_ _DE_G_ _F_ _ _

C++

Status PreCreateBiTree(BiTree &T)

{

char ch;

ch=getchar();

if(ch==' ')T=NULL;

else

{

if(!(T=(BiTNode *)malloc(sizeof(BiTNode))))exit(OVERFLOW);

T->data=ch;

PreCreateBiTree(T->lchild);

PreCreateBiTree(T->rchild);

}

return OK;

}

StatusPreCreateBiTree(BiTree&T)

{

charch;

ch=getchar();

if(ch==' ')T=NULL;

else

{

if(!(T=(BiTNode*)malloc(sizeof(BiTNode))))exit(OVERFLOW);

T->data=ch;

PreCreateBiTree(T->lchild);

PreCreateBiTree(T->rchild);

}

returnOK;

}

② 先序遍历(递归算法)

C++

Status PreOrderTraverse(BiTree T,Status(*Visit)(TElemType e))

{

if(T){

if(Visit(T->data))

if(PreOrderTraverse(T->lchild,Visit))

if(PreOrderTraverse(T->rchild,Visit))return OK;

return ERROR;

}else return OK;

}

StatusPreOrderTraverse(BiTreeT,Status(*Visit)(TElemTypee))

{

if(T){

if(Visit(T->data))

if(PreOrderTraverse(T->lchild,Visit))

if(PreOrderTraverse(T->rchild,Visit))returnOK;

returnERROR;

}elsereturnOK;

}

③ 中序遍历(递归算法)

C++

Status InOrderTraverse2(BiTree T,Status(*Visit)(TElemType e))

{

if(T){

InOrderTraverse2(T->lchild,Visit);

Visit(T->data);

InOrderTraverse2(T->rchild,Visit);

}

return OK;

}

StatusInOrderTraverse2(BiTreeT,Status(*Visit)(TElemTypee))

{

if(T){

InOrderTraverse2(T->lchild,Visit);

Visit(T->data);

InOrderTraverse2(T->rchild,Visit);

}

returnOK;

}

④ 中序遍历(非递归算法)

注意此处需要包含C++STL头文件include

C++

Status InOrderTraverse1(BiTree T,Status(*Visit)(TElemType e))

{

stackS;

BiTree p;

S.push(T);

while(!S.empty()){

while(p=S.top())S.push(p->lchild);

p=S.top();

S.pop();

if(!S.empty()){

p=S.top();

S.pop();

if(!Visit(p->data))return ERROR;

S.push(p->rchild);

}

return OK;

}

StatusInOrderTraverse1(BiTreeT,Status(*Visit)(TElemTypee))

{

stackS;

BiTreep;

S.push(T);

while(!S.empty()){

while(p=S.top())S.push(p->lchild);

p=S.top();

S.pop();

if(!S.empty()){

p=S.top();

S.pop();

if(!Visit(p->data))returnERROR;

S.push(p->rchild);

}

returnOK;

}

⑤ 后序遍历(递归算法)

C++

Status PostOrderTraverse(BiTree T,Status(*Visit)(TElemType e))

{

if(T){

PostOrderTraverse(T->lchild,Visit);

PostOrderTraverse(T->rchild,Visit);

Visit(T->data);

}

return OK;

}

StatusPostOrderTraverse(BiTreeT,Status(*Visit)(TElemTypee))

{

if(T){

PostOrderTraverse(T->lchild,Visit);

PostOrderTraverse(T->rchild,Visit);

Visit(T->data);

}

returnOK;

}

⑥ 层次遍历(使用QUEUE)

可以包含STL或者定义一个数组，使用循环队列即可。

C++

Status LevelOrderTraverse(BiTree T,Status(*Visit)(TElemType e))

{

BiTree p;

BiTNode *Q[100];

int front,rear;

front=rear=-1;

rear++;

Q[rear]=T;

while(front!=rear){

front=(front+1)%100;

p=Q[front];

Visit(p->data);

if(p->lchild!=NULL){

rear=(rear+1)%100;

Q[rear]=p->lchild;

}

if(p->rchild!=NULL){

rear=(rear+1)%100;

Q[rear]=p->rchild;

}

return OK;

}

StatusLevelOrderTraverse(BiTreeT,Status(*Visit)(TElemTypee))

{

BiTreep;

BiTNode*Q[100];

intfront,rear;

front=rear=-1;

rear++;

Q[rear]=T;

while(front!=rear){

front=(front+1)%100;

p=Q[front];

Visit(p->data);

if(p->lchild!=NULL){

rear=(rear+1)%100;

Q[rear]=p->lchild;

}

if(p->rchild!=NULL){

rear=(rear+1)%100;

Q[rear]=p->rchild;

}

returnOK;

}

⑦ Visit函数此处使用的是输出

C++

Status Visit(TElemType e)

{

printf("%c ",e);

return OK;

}

StatusVisit(TElemTypee)

{

printf("%c ",e);

returnOK;

}

⑧ 计算树的节点数

C++

Status CountNode(BiTree T,int &d)

{

if(T){

d++;

CountNode(T->lchild,d);

CountNode(T->rchild,d);

}

return OK;

}

StatusCountNode(BiTreeT,int&d)

{

if(T){

d++;

CountNode(T->lchild,d);

CountNode(T->rchild,d);

}

returnOK;

}

⑨ 计算树的深度

C++

Status GetDepth(BiTree T)

{

int hl,hr;

if(T==NULL)return 0;

else{

hl=GetDepth(T->lchild);

hr=GetDepth(T->rchild);

if(hl>hr)return hl+1;

else return hr+1;

}

StatusGetDepth(BiTreeT)

{

inthl,hr;

if(T==NULL)return0;

else{

hl=GetDepth(T->lchild);

hr=GetDepth(T->rchild);

if(hl>hr)returnhl+1;

elsereturnhr+1;

}

Main函数：

C++

int main()

{

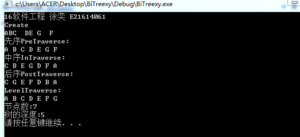
printf("16软件工程徐奕 E21614061\n");

printf("Create\n");

BiTree T;

PreCreateBiTree(T);

printf("先序PreTraverse:\n");

PreOrderTraverse(T,Visit);

printf("\n中序InTraverse:\n");

InOrderTraverse2(T,Visit);

printf("\n后序PostTraverse:\n");

PostOrderTraverse(T,Visit);

printf("\nLevelTraverse:\n");

LevelOrderTraverse(T,Visit);

printf("\n");

CountNode(T,d);

printf("\n节点数:%d\n",d);

printf("树的深度:%d\n",GetDepth(T));

system("pause");

return 0;

}

intmain()

{

printf("16软件工程徐奕 E21614061\n");

printf("Create\n");

BiTreeT;

PreCreateBiTree(T);

printf("先序PreTraverse:\n");

PreOrderTraverse(T,Visit);

printf("\n中序InTraverse:\n");

InOrderTraverse2(T,Visit);

printf("\n后序PostTraverse:\n");

PostOrderTraverse(T,Visit);

printf("\nLevelTraverse:\n");

LevelOrderTraverse(T,Visit);

printf("\n");

CountNode(T,d);

printf("\n节点数:%d\n",d);

printf("树的深度:%d\n",GetDepth(T));

system("pause");

return0;

}

实验小结

1. 遍历函数可以写成递归和非递归，递归函数更加简洁。

2. 层次遍历需要使用队列，可以包含C++STL或者定义一个数组，使用循环队列即可。注意每次判断时要把队列的头赋值给临时变量P，左右子树从队尾插入。

3.先序创建树时，要注意创建的时候如果没有左右子树要输入空格

输入：ABC_ _DE_G_ _F_ _ _

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。