树的基本概念

竞赛中常会出现的树的形式：

有序树：对于任意结点的多个子树严格按照从左到右的顺序排列
无序树：对于任意结点的子树之间无法确定顺序
有根树：树的根是确定的
无根树：树的根是不确定的，谁都有可能是树的根

树的存储方式

树的结构相对线性结构更为复杂，在存储时，既要存储树的值域，也要存储树的结点之间的关系。
树的存储方式有很多种，比如：双亲表示法，孩子表示法，孩子双亲表示法，孩子兄弟表示法等。
在此以孩子表示法举例，通过孩子表示法存储树结构，并在此基础上完成遍历。
注意：我们要存储的树都是无根树，根节点未知，所以在处理每一条边的时候，两种可能都要存储。比如题目给出 a - b ，那么我们既要存储b是a的子结点，又要存储a是b的子结点。
Q：这时候可能就有疑问了，如果说每个边的两种可能性都存储的话，那么如何完成遍历呢？会不会遍历多了一整倍的结点数量？
A：实际上并不会，因为我们在遍历的时候会给出一个根节点，然后按照根结点往下的顺序去遍历剩下的结点，并且我们会使用一个bool类型的数组去记录每个结点是否已经被遍历过了，如果被遍历过了就不会再遍历了。

vector数组实现

#include <iostream>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
vector<int> edges[N];
int n;

int main() 
{
	cin >> n; //给出n个节点 
	for(int i=1;i<n;i++) //读入n-1条边 
	{
		//a和b之间有一条边 
		int a,b; cin >> a >> b;
		edges[a].push_back(b);
		edges[b].push_back(a);
	}
	return 0;
}

链式前向星

//原则：当x有一个孩子y的时候，将y头插到x的链表中
#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int h[N],e[N*2],ne[N*2],id; //h数组中的第i位用来充当以i为首的链表的的头节点 ，e用来存放数据，ne用来存放孩子信息，相当于是很多个链表存储在了同一个数组中 

int n;

void push_front(int x,int y)
{
	id++;
	e[id] = y;
	ne[id] = h[x];
	h[x] = id; 
}

int main() 
{
	cin >> n; //给出n个节点 
	for(int i=1;i<n;i++)
	{
		int a,b; cin >> a >> b; //题目给出一组a和b，代表着a和b之间有一条边，但是不知道谁是谁的父亲节点，有两种可能，a是b的父节点，b是a的父节点，所以都要分别添加到他们自己的链表中
		push_front(a,b);
		push_front(b,a);
	}
	return 0;
} 

注意：vector数组实现是以尾插的方式添加结点，而链式前向星是以头插的方式添加结点

树的遍历

DFS

深度优先遍历，每次访问某个结点的子结点都尝试往更深的子结点去访问，说通俗点就是一条路走到黑。
流程是这样的：
1.从根节点出发，依次遍历每个子树
2.遍历子树的时候，重复第一步（将子树作为根结点，依次访问子树的子树）
这个“依次”就体现了深度优先，同时这个流程的特性（重复相同子问题）决定了DFS可以采用递归的方式去遍历。
递归的展开图就是一棵树
递归的过程就是对这颗树进行深度优先遍历

vector数组 DFS

#include <iostream>
#include <vector>
using namespace std;

const int N = 1e5 + 10;
vector<int> edges[N]; //存储树 
int n;

bool st[N]; //用来标记结点是否已经被遍历过了 

void dfs(int x)
{
	cout << x << " ";
	st[x] = true; //告诉全局的dfs这个点已经访问过了 
	for(auto v:edges[x])
	{
		if(!st[v]) dfs(v);
	}
}


int main() 
{
	//建树 
	cin >> n; //给出n个节点 
	for(int i=1;i<n;i++) //读入n-1条边 
	{
		//a和b之间有一条边 
		int a,b; cin >> a >> b;
		edges[a].push_back(b);
		edges[b].push_back(a);
	}
	
	//深度优先遍历 
	dfs(1); //假设1为根节点，以1为根dfs遍历 
	
	return 0;
}

链式前向星 DFS

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
int id,e[N*2],ne[N*2],h[N];//存储树 
int n;

bool st[N]; //用来标记结点是否已经被遍历过了 

void dfs(int x)
{
	cout << x << " ";
	st[x] = true;
	for(int i = h[x];i;i=ne[i])
	{
		int v = e[i]; //孩子 
		if(!st[v]) 
		{
//			cout << v << " ";
			dfs(v); 
		}
	}
}

void add(int x,int y) //这个add函数就是头插
{
	id++;
	e[id] = y;
	ne[id] = h[x];
	h[x] = id;
} 

int main() 
{
	//建树  //将a的子节点b头插到a的链表中 
	cin >> n;
	for(int i=1;i<n;i++)
	{
		int a,b; cin >> a >> b;
		add(a,b); add(b,a);
	}
	//深度优先遍历
	dfs(1); //还是假设1为根 
	
	
	return 0;
}

测试用例

11
1 3
7 3
3 10
1 5
4 5
2 1
11 2
6 11
11 8
11 9

测试结果
1.vector数组实现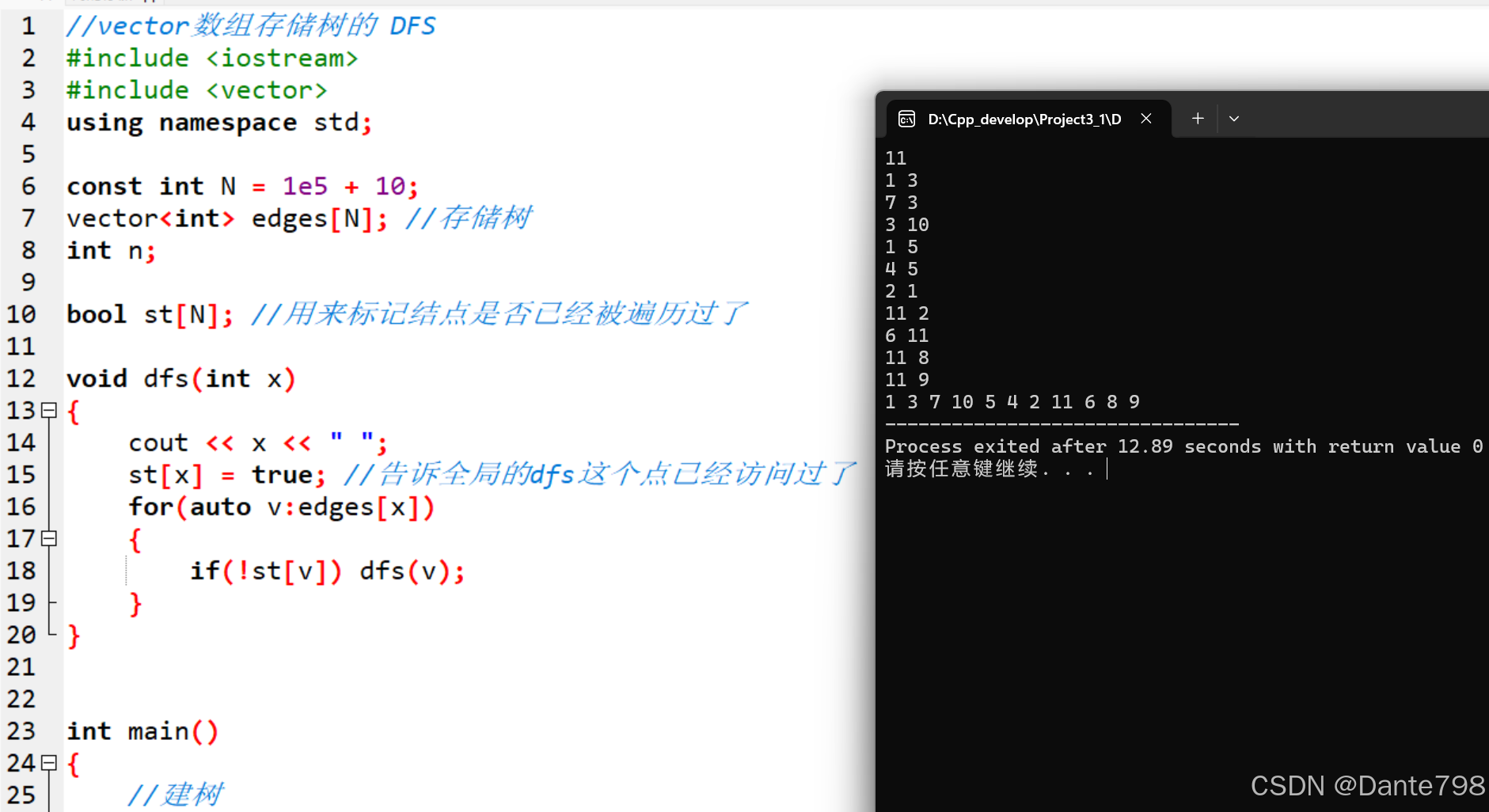

2.链式前向星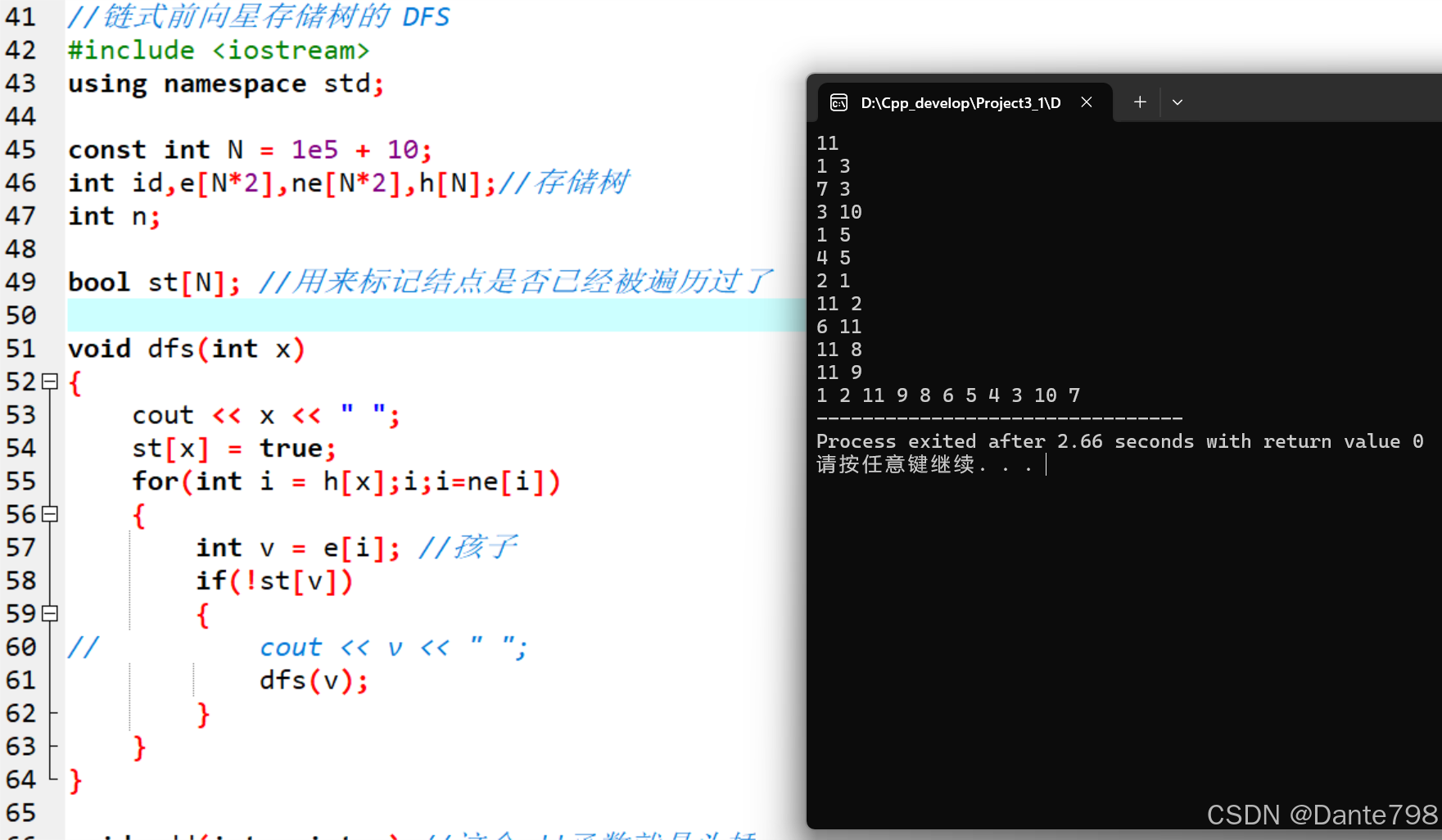

我们可以看到测试结果是完全不同的，难道是出错了吗？
其实不是，我们前面就提到过，一个是用尾插的方式添加结点，一个是用头插的方式添加结点，所以在遍历的时候，它们从左到右的顺序是完全相反的，但是结果都是正确的。

这是这个数本身的样子：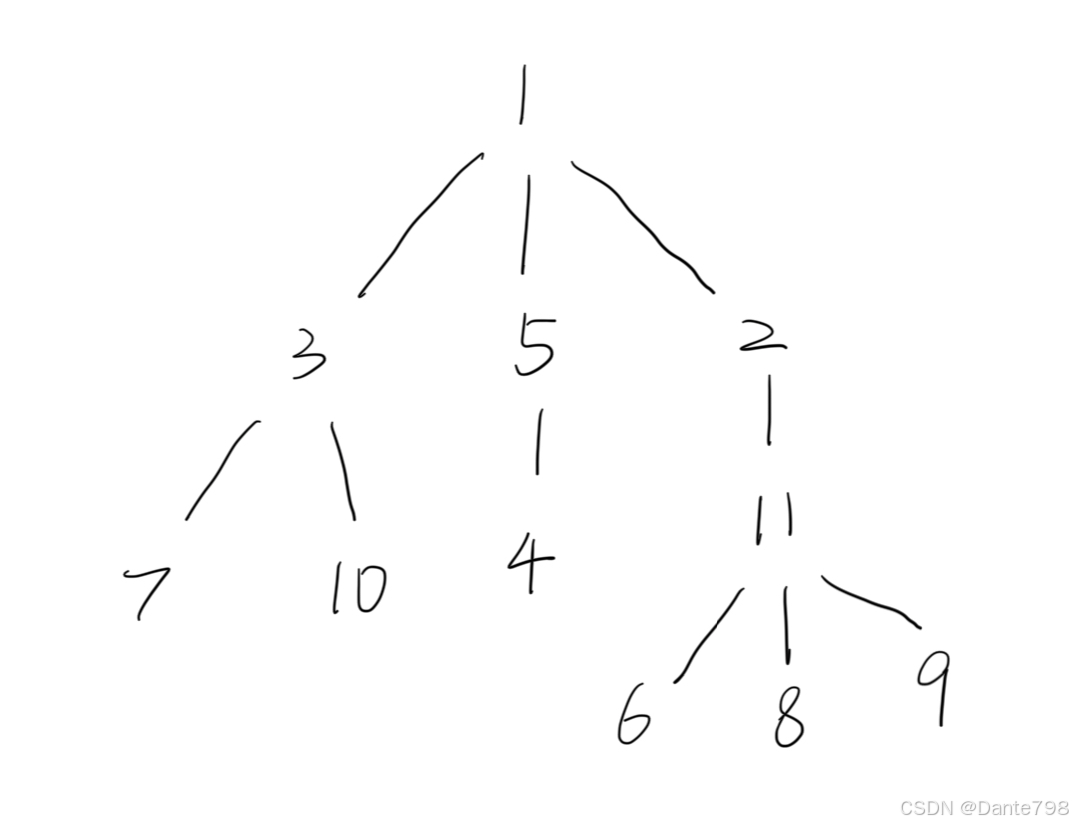

BFS

Breadth First Search 广度优先遍历，也叫层序遍历，每次访问同一层的所有结点。
bfs是通过队列来实现的。

vector数组存储树中的BFS

#include<iostream>
#include<vector>
#include<queue> 
using namespace std;

const int N = 1e5 + 10;
vector<int> edges[N]; 
bool st[N];
int n;
 
void bfs()
{
	queue<int> q; //队列的定义可以放到bfs函数内，因为在其他全局的地方用不上这个队列，仅仅是bfs的实现需要队列
	//这一部分是针对根节点的入队和标记操作 
	q.push(1); //这个1也可以作为参数传入bfs 
	st[1] = true;
	
	while(q.size()) //这有一个外层循环，当队列还有元素的时候就会一直执行 
	{
		int t = q.front(); q.pop();
		cout << t << " ";
		
		for(auto v:edges[t]) //实际上遍历t的结点不只是t的子结点，因为我们是针对无根树进行的存储，这里还会遍历到t的父结点，所以标记已经入队的结点相当重要，不然就会陷入死循环 
		{
			if(!st[v])
			{
				q.push(v); //只要入队，就要在st中标记这个结点 
				st[v] = true;
			}	
		} 
	}
}
 
int main()
{
	cin >> n; 
	for(int i=1;i<n;i++)
	{
		int a,b; cin >> a >> b;
		edges[a].push_back(b);
		edges[b].push_back(a);   
	}
	bfs();
	return 0;
}

链式前向星 BFS

#include<iostream>
#include<queue>
using namespace std;

const int N = 1e5 + 10;
int id,h[N],e[N*2],ne[N*2];
int n;
bool st[N];

void add(int a, int b)
{
	id++;
	e[id] = b;
	ne[id] = h[a];
	h[a] = id;
}

void bfs()
{
	queue<int> q;
	q.push(1);
	st[1] = true;
	while(q.size())
	{
		int t = q.front(); q.pop();
		cout << t << " ";
		for(int i=h[t];i;i=ne[i])
		{
			if(!st[e[i]])
			{
				q.push(e[i]);
				st[e[i]] = true;
			} 
		}
	}
}

int main()
{
	//建树 
    cin >> n;
    for(int i=1;i<n;i++)
    {
    	int a,b; cin >> a >> b;
    	add(a,b); add(b,a);
	}
	//BFS遍历 
	bfs();
	return 0;
}

运行结果

1.vector数组实现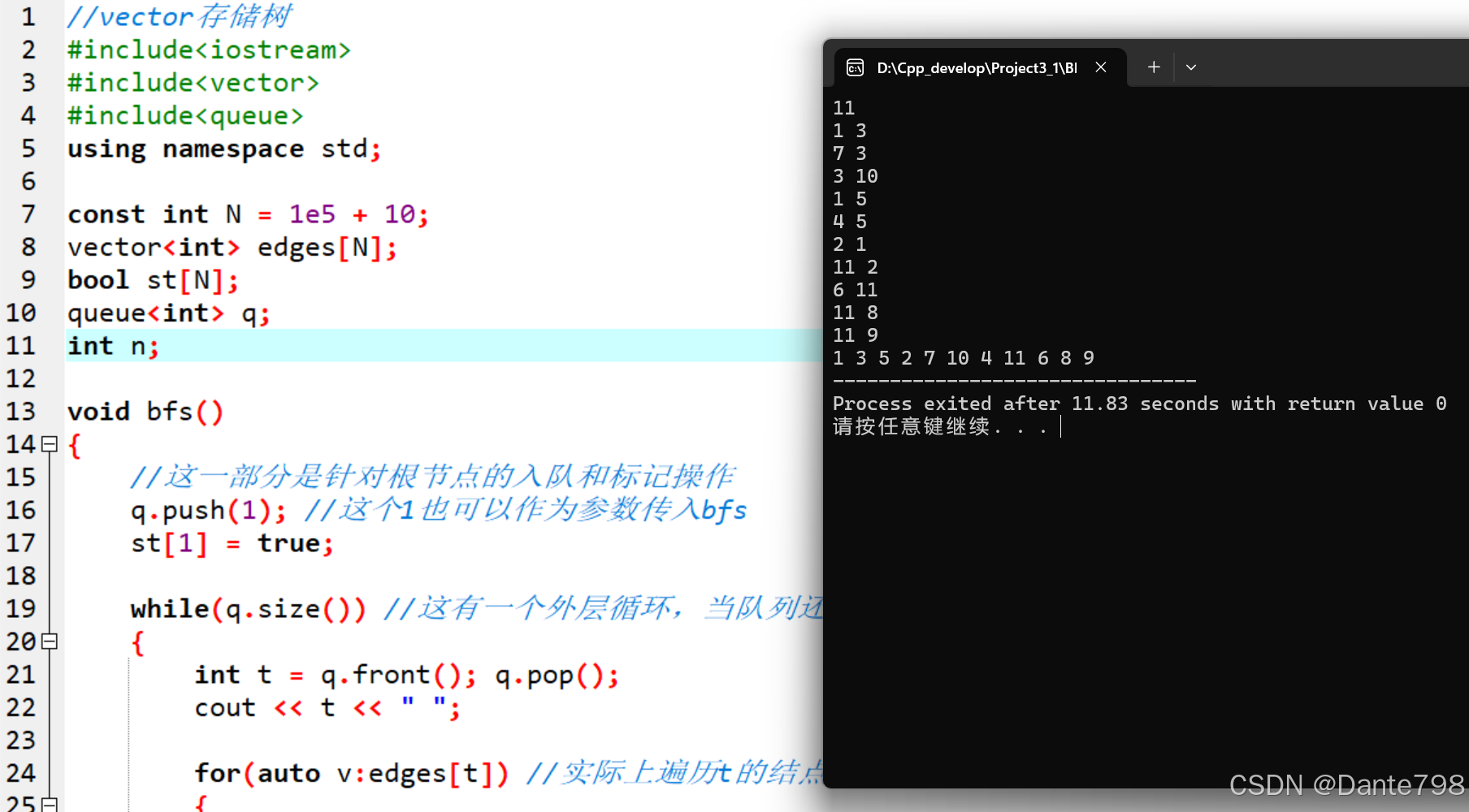

2.链式前向星实现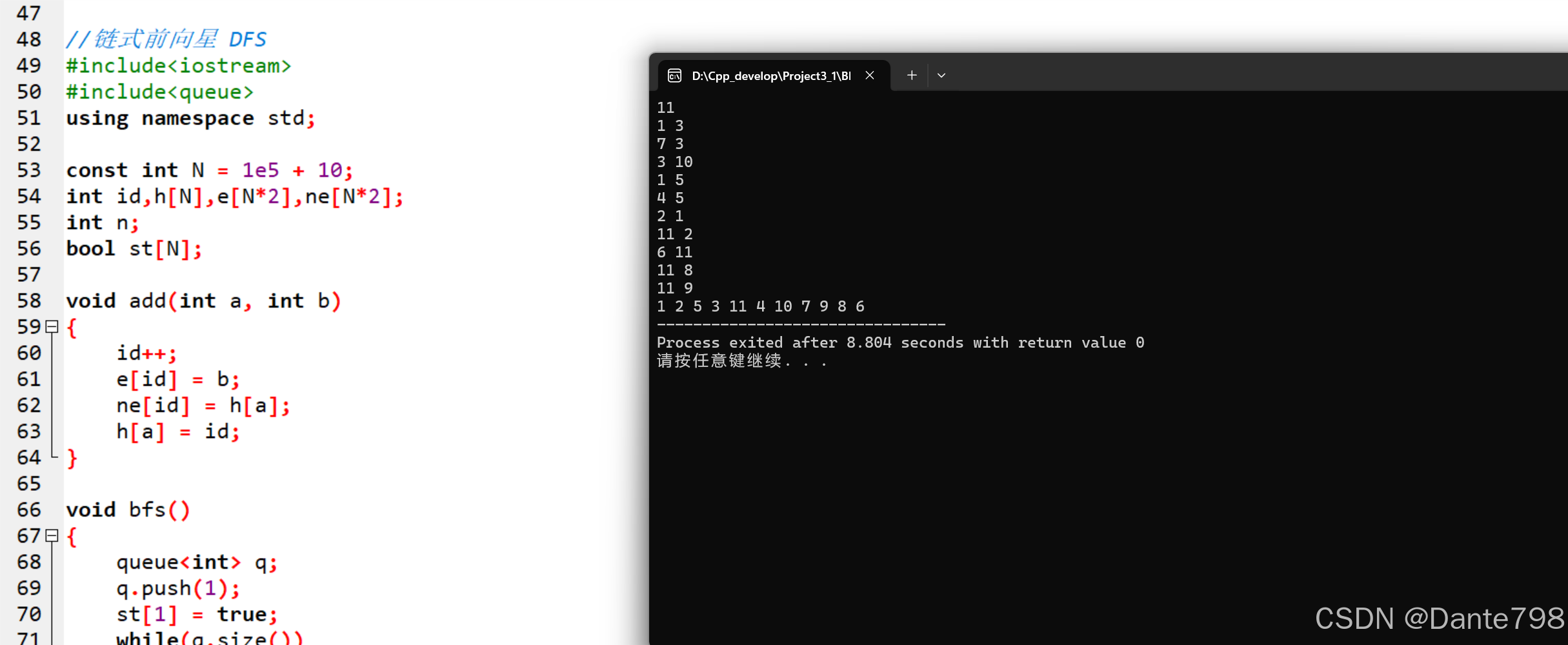

可以看到他们的结果在每一层子节点上是相反的，这也是插入结点方式的不同导致的