Python数据分析与应用

Koonan-Edogawa

1201人浏览 · 2023-02-23 13:08:03

Koonan-Edogawa · 2023-02-23 13:08:03 发布

文章目录

第1章 Numpy数值计算基础
第2章 Matplotlib数据可视化基础
第4章使用scikit-learn构建模型
第5章航空公司客户价值分析
第6章财政收入预测分析

第1章 Numpy数值计算基础

1.1 创建数组对象

1.1.1 数组的属性

属性	说明
ndim	数组维度
shape	数组尺寸
size	数组元素总和
dtype	数组中元素的类型

1.1.2 数组创建

import numpy as np
np.array([[1,2],[3,4]])

函数	说明与使用
arange	np.arange(0,1,0.1)
linspace	创建指定元素数量的数组 np.linspace(0,1,5)
logspace	创建指定等比数列 np.logspace(0,2,20)

函数	用法
zeros	np.zeros((2,3))
eye	np.eye(3)
diag	np.diag([1,2,3,4])
ones	np.ones((3,4))

1.2 生成随机数

import numpy as np
np.random.random(100)

函数	说明与使用
rand	均匀分布 np.random.rand(10,5)
randn	正态分布 np.random.randn(2,3)
randint	生成整数 np.random.randint(1,10,size=[2,6])

1.3 变换数组的形态

1.3.1 reshape

import numpy as np
arr = np.arange(12)
arr.reshape(3,4)

1.3.2 hstack 横向组合

import numpy as np
arr1 = np.arange(12).reshape(3,4)
arr2 = arr1 * 3
np.hstack((arr1, arr2))

1.3.3 vstack 纵向组合

import numpy as np
arr1 = np.arange(12).reshape(3,4)
arr2 = arr1 * 3
np.vstack((arr1, arr2))

1.4 创建矩阵

import numpy as np
np.matrix([[1,2,3],[4,5,6],[7,8,9]])

属性	含义
T	转置
H	共轭转置
I	逆矩阵

注：np.all表示逻辑 and ；np.any表示逻辑or

1.5 读/写文件

np.savetext(“文件路径”,“数据”) 可加载csv文件
np.loadtext(“文件路径”)

1.6 排序与搜索

1.6.1 sort 直接排序

np.random.seed(10)
arr = np.random.randint(1,10,size=7)
arr.sort()
print(arr)

1.6.2 argsort 返回重新排序值的下标

np.random.seed(10)
arr = np.random.randint(1,10,size=7)
arr.argsort()

1.6.3 lexsort 多个键值排序时按最后一个排序

a = np.array([3,2,4,5,6])
b = np.array([12,53,83,12,57])
c = np.array([100,200,300,500,400])
d = np.lexsort((a,b,c)) # 返回排序后的下标
list(zip(a[d],b[d],c[d]))

1.6.4 where 返回满足给定条件的元素索引

import numpy as np
arr = np.arange(12).reshape(3,4)
np.where(arr>5)

1.7 去重与重复数据

unique 去重
tile(“数据”,“次数”) 对数组进行重复
repeat(“数据”,“次数”,“维度”) 对数组的元素进行重复

1.8 常用统计函数

函数	特殊解释
sum mean std var min max	使用axis参数指定维度
argmin argmax	返回对应值的索引
cumsum cumprod	累计和与累计积

第2章 Matplotlib数据可视化基础

2.1 掌握绘图基础语法和常用参数

import matplotlib.pyplot as plt

2.1.1 创建画布与创建子图

函数	解释
plt.figure()	创建空白画布
figure.add_subplot()	创建并选中子图

2.1.2 添加画布内容

函数	解释
plt.title()	添加标题
plt.xlabel()	添加x轴名称
plt.ylabel()	添加y轴名称
plt.xlim()	指定x轴的范围
plt.ylim()	指定y轴的范围
plt.xticks()	指定x轴刻度的数目与取值
plt.yticks()	指定y轴刻度的数目与取值
plt.legend()	指定当前图形的图例
plt.text(‘x’,‘y’,‘文本’)	添加文本

2.1.3 保存与显示图形

函数	解释
plt.savafig()	保存绘制的图形
plt.show()	显示图形

2.1.4 预设风格

import matplotlib.pyplot as plt
plt.style.available # 查看预设风格

2.1.5 rc参数

plt.rcParams['lines.linestyle'] = '-.'

函数	解释
plt.rcParams	查看rc默认参数
lines.linewidth	线条宽度
lines.linestyle	线条样式
lines.marker	线条上点的形状
lines.markersize	点的大小

2.1.6 显示中文标题

plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_miuns'] = False # 设置正常显示符号

2.2 分析特征间关系

2.2.1 散点图：了解特征间的相关关系

plt.scatter('x','y',s='点的大小',c='点的颜色',
			marker='点的类型',alpha='点的透明度')

2.2.2 折线图：了解特征间的趋势关系（一次接收多组数据）

plt.plot('x','y',color='点的颜色',linestyle='线条类型',
			marker='点的类型',alpha='点的透明度')

2.2.3 直方图：数据的频数情况（定量数据）

plt.hist('数据',bins='长方形数',range='数据范围',
		normed='频率/频数',rwidth='长方形宽度')

2.2.4 条形图：数据的数量情况（分类数据）

plt.bar(left='x轴数据',height='x轴数据的数量',
		width='直方图宽度',color='直方图颜色')

2.2.5 饼图：数据的占比情况

plt.pie('数据')

函数	说明
explode	指定项距离饼图圆心为n个半径
labels	每一项的名称
color	饼图的颜色
autopct	数值的显示方式
pctdistance	指定每一项的autopct和距离圆心的半径
labeldistance	指定每一项名称label和距离圆心的半径0
radius	饼图的半径

2.2.6 箱线图：数据的分散情况

plt.boxplot('数据')

函数	用法
notch	箱体中间是否有缺口
sym	异常点的形状
vert	图形是横向还是纵向
positions	图形位置
widths	每个箱体的宽度
labels	每个箱体的标签
meanline	是否显示均值线

第4章使用scikit-learn构建模型

4.1 使用sklearn转换器处理数据

4.1.1 加载datasets模块中的数据集

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
cancer_data = cancer.data
cancer_target = cancer.target
cancer_names = cancer.feature_names
print('原始数据集数据的形状为：',cancer_data.shape)
print('原始数据集标签的形状为：',cancer_target.shape)

4.1.2 将数据集划分为训练集和测试集

from sklearn.model_selection import train_test_split
cancer_data_train, cancer_data_test,cancer_target_train, \
cancer_target_test = train_test_split(cancer_data, 
    cancer_target, test_size=0.2, random_state=42)
print('训练集数据的形状为：',cancer_data_train.shape)
print('测试集数据的形状为：',cancer_data_test.shape)
print('训练集标签的形状为：',cancer_target_train.shape)
print('测试集标签的形状为：',cancer_target_test.shape)

4.1.3 数据预处理

import numpy as np
from sklearn.preprocessing import MinMaxScaler
Scaler = MinMaxScaler().fit(cancer_data_train) # 生成规则
cancer_trainScaler = Scaler.transform(cancer_data_train) 
print('离差标准化前训练集数据的最小值为：',np.min(cancer_data_train))
print('离差标准化前训练集数据的最大值为：',np.max(cancer_data_train))
print('离差标准化后训练集数据的最小值为：',np.min(cancer_trainScaler))
print('离差标准化后训练集数据的最大值为：',np.max(cancer_trainScaler))
cancer_testScaler = Scaler.transform(cancer_data_test)
print('离差标准化前测试集数据的最小值为：',np.min(cancer_data_test))
print('离差标准化前测试集数据的最大值为：',np.max(cancer_data_test))
print('离差标准化后测试集数据的最小值为：',np.min(cancer_testScaler))
print('离差标准化后测试集数据的最大值为：',np.max(cancer_testScaler))

函数名称	说明
StandardScaler	标准差标准化
Normalizer	归一化
Binarizer	对定量特征进行二值化处理
OneHotEncoder	对定性特征进行独热编码处理

4.1.4 降维PCA

from sklearn.decomposition import PCA
pca_model = PCA(n_components=10).fit(cancer_trainScaler) # 生成规则
cancer_trainPca = pca_model.transform(cancer_trainScaler) # 将规则应用于训练集
print('PCA降维前训练集数据的形状为：',cancer_trainScaler.shape)
print('PCA降维后训练集数据的形状为：',cancer_trainPca.shape)
cancer_testPca = pca_model.transform(cancer_testScaler) # 将规则应用于测试集
print('PCA降维前测试集数据的形状为：',cancer_testScaler.shape)
print('PCA降维后测试集数据的形状为：',cancer_testPca.shape)

4.2 构建并评价聚类模型

4.2.1 使用sklearn估计器构建聚类模型

from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.cluster import KMeans
iris = load_iris()
iris_data = iris['data'] # 提取数据集中的特征
iris_target = iris['target'] # 提取数据集中的标签
iris_names = iris['feature_names'] # 提取特征名
scale = MinMaxScaler().fit(iris_data)# 训练规则
iris_dataScale = scale.transform(iris_data) # 应用规则
kmeans = KMeans(n_clusters=3,random_state=123).fit(iris_dataScale)
print('构建的K-Means模型为：\n',kmeans)
result = kmeans.predict([[1.5,1.5,1.5,1.5]])
print('花瓣花萼长度宽度全为1.5的鸢尾花预测类别为：', result[0])

4.2.2 聚类结果可视化

import pandas as pd
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
df = PCA(n_components=2).fit_transform(iris_data)
df = pd.DataFrame(df)
df['labels'] = kmeans.labels_
# 提取不同标签的数据
df1 = df[df['labels'] == 0]
df2 = df[df['labels'] == 1] 
df3 = df[df['labels'] == 2] 
fig = plt.figure(figsize=(9, 6)) 
plt.plot(df1[0],df1[1],'bo',df2[0],df2[1],'r*',df3[0],df3[1],'gD')
plt.show() # 显示图片

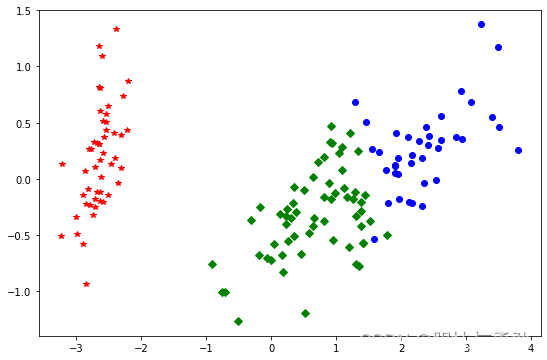
在这里插入图片描述

4.2.3 评价聚类模型

方法名称	真实值	最佳值	sklearn函数
ARI评价法（兰德系数）	需要	1.0	adjusted_rand_score
AMI评价法（互信息）	需要	1,0	adjusted_mutual_info_score
V-measure评分	需要	1.0	completeness_score
FMI评价法	需要	1.0	fowlkes_mallows_score
轮廓系数评价法	不需要	畸变程度最大	silhouette_score
Calinski-Harabasz指数评价法	不需要	相较最大	calinski_harabaz_score

4.2.3.1 使用FMI评价法评价K-means聚类模型

from sklearn.metrics import fowlkes_mallows_score
for i in range(2, 7):
    kmeans = KMeans(n_clusters=i, random_state=123).fit(iris_data)
    score = fowlkes_mallows_score(iris_target, kmeans.labels_)
    print('iris数据聚%d类FMI评价分值为：%f' %(i,score))

4.2.3.2 使用轮廓系数法评价K-means聚类模型

from sklearn.metrics import silhouette_score
import matplotlib.pyplot as plt
silhouettteScore = []
for i in range(2,15):
    kmeans = KMeans(n_clusters=i, random_state=123).fit(iris_data)
    score = silhouette_score(iris_data, kmeans.labels_)
    silhouettteScore.append(score)
plt.figure(figsize=(10,6))
plt.plot(range(2,15),silhouettteScore,linewidth=1.5, linestyle="-")
plt.show()

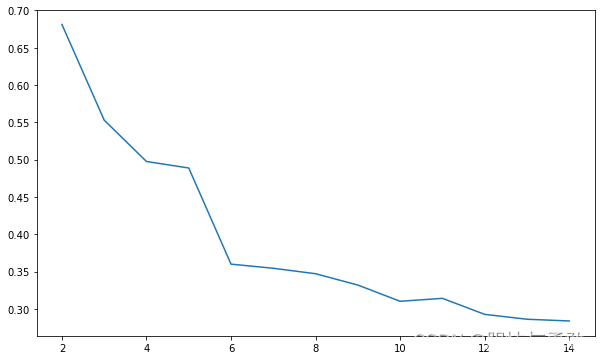
在这里插入图片描述

4.2.3.3 使用calinski_harabasz指数评价K-means聚类模型

from sklearn.metrics import calinski_harabasz_score
for i in range(2,7):
    kmeans = KMeans(n_clusters=i, random_state=123).fit(iris_data)
    score = calinski_harabasz_score(iris_data, kmeans.labels_)
    print('iris数据聚%d类calinski_harabasz指数为：%f'%(i,score))

4.3 构建并评价分类模型

模块名称	函数名称	算法名称
linear_model	LogisticRegression	逻辑斯蒂回归
svm	SVC	支持向量机
neighbors	KNeighborsClassifier	K最近邻分类
naive_bayes	GaussianNB	高斯朴素贝叶斯
tree	DesisionTreeClassifier	分类决策树
ensemble	RandomForestClassifier	随机森林分类
ensemble	GranientBoostingClassifier	梯度提升分类树

4.3.1 使用sklearn估计器构建分类模型

import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
cancer = load_breast_cancer()
cancer_data = cancer['data']
cancer_target = cancer['target']
cancer_names = cancer['feature_names']
# 将数据划分为训练集测试集
cancer_data_train,cancer_data_test,cancer_target_train, \
cancer_target_test = train_test_split(cancer_data,
    cancer_target, test_size = 0.2,random_state = 22)
# 数据标准化
stdScaler = StandardScaler().fit(cancer_data_train)
cancer_trainStd = stdScaler.transform(cancer_data_train)
cancer_testStd = stdScaler.transform(cancer_data_test)
# 建立SVM模型
svm = SVC().fit(cancer_trainStd,cancer_target_train)
print('建立的SVM模型为：\n',svm)
# 预测训练集结果
cancer_target_pred = svm.predict(cancer_testStd)
print('预测前20个结果为：\n',cancer_target_pred[:20])
# 分类结果的混淆矩阵与准确率
true = np.sum(cancer_target_pred == cancer_target_test)
print('预测对的结果数目为：', true)
print('预测错的的结果数目为：', cancer_target_test.shape[0]-true)
print('预测结果准确率为：', true/cancer_target_test.shape[0])

4.3.2 评价分类模型

方法名称	最佳值	sklearn函数
Precision(精确率)	1,0	metrics.precision_score
Recall(召回率)	1.0	metrics.recall_score
F1值	1.0	metrics.f1_score
Cohen’s Kappa系数	1.0	metrics.cohen_kappa_score
ROC曲线	靠近y轴	metrics.roc_curve

4.3.2.1 分类模型常用评价方法

from sklearn.metrics import accuracy_score,precision_score, \
recall_score,f1_score,cohen_kappa_score
print('使用SVM预测breast_cancer数据的准确率为：',
      accuracy_score(cancer_target_test, cancer_target_pred))
print('使用SVM预测breast_cancer数据的精确率为：',
      precision_score(cancer_target_test, cancer_target_pred))
print('使用SVM预测breast_cancer数据的召回率为：',
      recall_score(cancer_target_test, cancer_target_pred))
print('使用SVM预测breast_cancer数据的F1值为：',
      f1_score(cancer_target_test, cancer_target_pred))
print('使用SVM预测breast_cancer数据的Cohen’s Kappa系数为：',
      cohen_kappa_score(cancer_target_test, cancer_target_pred))

4.3.2.2 分类模型评价报告

from sklearn.metrics import classification_report
print('使用SVM预测iris数据的分类报告为：','\n',
      classification_report(cancer_target_test,cancer_target_pred))

4.3.2.3 绘制ROC曲线

from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
# 求出ROC曲线的x轴和y轴
fpr,tpr,thresholds = roc_curve(cancer_target_test,cancer_target_pred)
plt.figure(figsize=(10,6))
plt.xlim(0,1) # 设定x轴的范围
plt.ylim(0.0,1.1) # 设定y轴的范围
plt.xlabel('False Postive Rate')
plt.ylabel('True Postive Rate')
plt.plot(fpr,tpr,linewidth=2, linestyle="-",color='red')
plt.show()

在这里插入图片描述

4.4 构建并评价回归模型

4.4.1 使用sklearn估计器构建线性回归模型

from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
# 加载boston数据
boston = load_boston()
X = boston['data']
y = boston['target']
names = boston['feature_names']
# 将数据划分为训练集测试集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size = 0.2,random_state=125)
# 建立线性回归模型
clf = LinearRegression().fit(X_train,y_train)
print('建立的LinearRegression模型为：','\n',clf)
# 预测训练集结果
y_pred = clf.predict(X_test)
print('预测前20个结果为：','\n',y_pred[:20])

4.4.2 回归结果可视化

import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.sans-serif'] = 'SimHei'
fig = plt.figure(figsize=(10,6))
# 用不同的颜色表示不同数据
plt.plot(range(y_test.shape[0]),y_test,color="blue", linewidth=1.5, linestyle="-")
plt.plot(range(y_test.shape[0]),y_pred,color="red", linewidth=1.5, linestyle="-.")
plt.legend(['真实值','预测值']) 
plt.show() # 显示图片

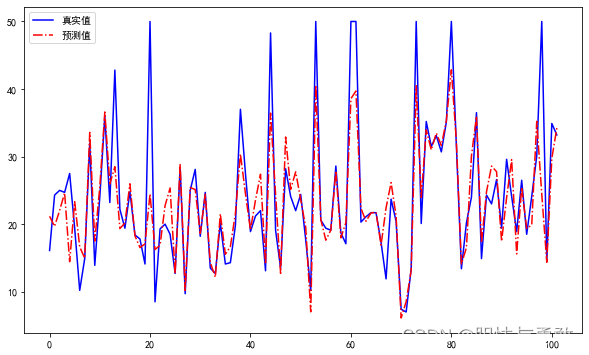
在这里插入图片描述

4.4.3 评价回归模型

方法名称	sklearn函数
平均绝对标准误	metrice.mean_absolute_erro
均方误差	metrice.mean_squared_error
中值绝对误差	metrice.median_absolute_error
可解释方差值	metrice.explained_variance_score
R平方值	metrice.r2_score

from sklearn.metrics import explained_variance_score,\
mean_absolute_error,mean_squared_error,\
median_absolute_error,r2_score
print('Boston数据线性回归模型的平均绝对误差为：',mean_absolute_error(y_test,y_pred))
print('Boston数据线性回归模型的均方误差为：',mean_squared_error(y_test,y_pred))
print('Boston数据线性回归模型的中值绝对误差为：',median_absolute_error(y_test,y_pred))
print('Boston数据线性回归模型的可解释方差值为：',explained_variance_score(y_test,y_pred))
print('Boston数据线性回归模型的R方值为：',r2_score(y_test,y_pred))

第5章航空公司客户价值分析

5.1 了解航空公司现状与客户价值分析

抽取航空公司2012年4月1日至2014年3月31日的数据
对抽取的数据进行数据清洗、特征构建和标准化等操作
基于RFM模型，使用K-Means算法进行客户分群

5.2 缺失值与异常值处理

import numpy as np
import pandas as pd
airline_data = pd.read_csv("./data/air_data.csv",encoding="gb18030")
print('原始数据的形状为：',airline_data.shape)
# 去除票价为空的记录
exp1 = airline_data["SUM_YR_1"].notnull()
exp2 = airline_data["SUM_YR_2"].notnull()
exp = exp1 & exp2
airline_notnull = airline_data.loc[exp,:]
print('删除缺失记录后数据的形状为：',airline_notnull.shape)
# 只保留票价非零的，且平均折扣率不为0且总飞行公里数大于0的记录。
index1 = airline_notnull['SUM_YR_1'] != 0
index2 = airline_notnull['SUM_YR_2'] != 0
index3 = (airline_notnull['SEG_KM_SUM']> 0) & \
    (airline_notnull['avg_discount'] != 0)
airline = airline_notnull[(index1 | index2) & index3]
print('删除异常记录后数据的形状为：',airline.shape)

5.3 选取并构建LRFMC模型的5个特征

airline_selection = airline[["FFP_DATE","LOAD_TIME",
    "FLIGHT_COUNT","LAST_TO_END","avg_discount","SEG_KM_SUM"]]
# 构建L特征
L = pd.to_datetime(airline_selection["LOAD_TIME"]) - \
        pd.to_datetime(airline_selection["FFP_DATE"])
L = L.astype("str").str.split().str[0]
L = L.astype("int") / 30
# 合并特征
airline_features = pd.concat([L,airline_selection.iloc[:,2:]],axis=1)
print('构建的LRFMC特征前5行为：\n',airline_features.head())
# 标准化LRFMC模型的特征
from sklearn.preprocessing import StandardScaler
data = StandardScaler().fit_transform(airline_features)
print('标准化后LRFMC五个特征为：\n',data[:5,:])

5.4 使用K-Means算法进行客户分群

常用参数	说明
n_clusters	分类簇的数量
max_iter	最大迭代次数
n_init	算法运行次数
init	初始点的选取

属性	说明
cluster_centers_	分类簇的均值向量
labels_	每个样本所属簇的标记
Inertia_	每个样本距离他们各自最近簇中心之和

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans # 导入kmeans算法
airline_scale = np.load('./tmp/airline_scale.npz')['arr_0']
k = 5 # 确定聚类中心数
# 构建模型
kmeans_model = KMeans(n_clusters = k,random_state=123)
fit_kmeans = kmeans_model.fit(airline_scale)   # 模型训练
print(kmeans_model.cluster_centers_) # 查看聚类中心
print(kmeans_model.labels_) # 查看样本的类别标签
# 统计不同类别样本的数目
r1 = pd.Series(kmeans_model.labels_).value_counts()
print('最终每个类别的数目为：\n',r1)

第6章财政收入预测分析

6.1 了解财政收入预测的背景和方法

分析、识别影响地方财政收入的关键特征
预测2014年和2015年的财政收入

6.2 分析财政收入数据特征的相关性

import numpy as np
import pandas as pd
inputfile = './data/data.csv'
data = pd.read_csv(inputfile) # 读取数据
# 保留两位小数
print('相关系数矩阵为：',np.round(data.corr(method='pearson'), 2))

6.3 使用Lasso回归选取财政收入预测的关键特征

import numpy as np
import pandas as pd
from sklearn.linear_model import Lasso
inputfile = './data/data.csv'
data = pd.read_csv(inputfile) # 读取数据
lasso = Lasso(1000,random_state=1234)  # 调用Lasso()函数，设置λ的值为1000
lasso.fit(data.iloc[:,0:13],data['y'])
print('相关系数为：',np.round(lasso.coef_,5))  # 输出结果，保留五位小数

6.4 计算相关系数非零的个数

print('相关系数非零个数为：',np.sum(lasso.coef_ != 0))
mask = lasso.coef_ != 0  # 返回一个相关系数是否为零的布尔数组
print('相关系数是否为零：',mask)
new_reg_data = data.iloc[:,:13].iloc[:, mask]  # 返回相关系数非零的数据
print('输出数据的维度为：',new_reg_data.shape)  # 查看输出数据的维度

6.5 使用SVR构建财政收入预测模型

参数名称	说明
epsilon	用于loss参数中的参数
tol	终止迭代的阈值
C	罚项系数
loss	损失函数
fit_intercept	是否计算模型的截距
max_iter	最大迭代次数

属性名称	说明
coef_	给出各个特征的权重
intercept_	决策函数中的常数项

import pandas as pd
import numpy as np
from sklearn.svm import LinearSVR
import matplotlib.pyplot as plt
from sklearn.metrics import explained_variance_score,\
        mean_absolute_error,mean_squared_error,\
        median_absolute_error,r2_score
inputfile = './tmp/new_reg_data_GM11.csv'
data = pd.read_csv(inputfile) # 读取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
data_train = data.iloc[:20,:].copy() # 取2014年前的数据建模
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean) / data_std # 数据标准化
x_train = data_train[feature].values # 特征数据
y_train = data_train['y'].values # 标签数据
linearsvr = LinearSVR()   # 调用LinearSVR()函数
linearsvr.fit(x_train, y_train)
# 预测，并还原结果
x = ((data[feature] - data_mean[feature])/ data_std[feature]).values
data[u'y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
print('真实值与预测值分别为：',data[['y','y_pred']])
print('预测图为：',data[['y','y_pred']].plot(subplots=True,style=['b-o','r-*']))
plt.show()

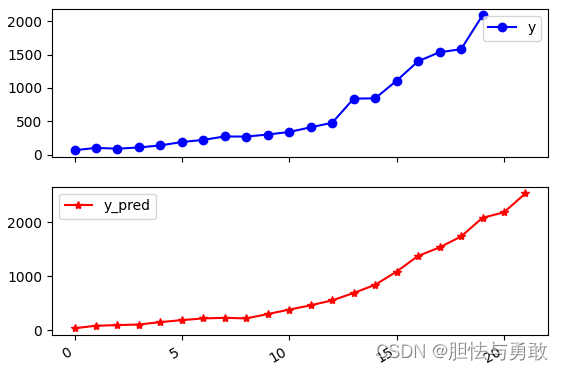
在这里插入图片描述

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

大数据毕业设计选题推荐-基于大数据的农作物产量数据分析与可视化系统-Hadoop-Spark-数据可视化-BigData

魔乐社区

大模型推理适配实战：手把手带你完成vLLM Ascend迁移实操

魔乐社区

基于python大数据的汽车数据分析系统设计与实现

魔乐社区

所有评论(0)

查看更多评论

Koonan-Edogawa

@qq_52652401

已为社区贡献1条内容

Python数据分析与应用

Koonan-Edogawa

文章目录

第1章 Numpy数值计算基础

1.1 创建数组对象

1.1.1 数组的属性

1.1.2 数组创建

1.2 生成随机数

1.3 变换数组的形态

1.3.1 reshape

1.3.2 hstack 横向组合

1.3.3 vstack 纵向组合

1.4 创建矩阵

1.5 读/写文件

1.6 排序与搜索

1.6.1 sort 直接排序

1.6.2 argsort 返回重新排序值的下标

1.6.3 lexsort 多个键值排序时按最后一个排序

1.6.4 where 返回满足给定条件的元素索引

1.7 去重与重复数据

1.8 常用统计函数

第2章 Matplotlib数据可视化基础

2.1 掌握绘图基础语法和常用参数

2.1.1 创建画布与创建子图

2.1.2 添加画布内容

2.1.3 保存与显示图形

2.1.4 预设风格

2.1.5 rc参数

2.1.6 显示中文标题

2.2 分析特征间关系

2.2.1 散点图：了解特征间的相关关系

2.2.2 折线图：了解特征间的趋势关系（一次接收多组数据）

2.2.3 直方图：数据的频数情况（定量数据）

2.2.4 条形图：数据的数量情况（分类数据）

2.2.5 饼图：数据的占比情况

2.2.6 箱线图：数据的分散情况

第4章 使用scikit-learn构建模型

4.1 使用sklearn转换器处理数据

4.1.1 加载datasets模块中的数据集

4.1.2 将数据集划分为训练集和测试集

4.1.3 数据预处理

4.1.4 降维PCA

4.2 构建并评价聚类模型

4.2.1 使用sklearn估计器构建聚类模型

4.2.2 聚类结果可视化

4.2.3 评价聚类模型

4.2.3.1 使用FMI评价法评价K-means聚类模型

4.2.3.2 使用轮廓系数法评价K-means聚类模型

4.2.3.3 使用calinski_harabasz指数评价K-means聚类模型

4.3 构建并评价分类模型

4.3.1 使用sklearn估计器构建分类模型

4.3.2 评价分类模型

4.3.2.1 分类模型常用评价方法

4.3.2.2 分类模型评价报告

4.3.2.3 绘制ROC曲线

4.4 构建并评价回归模型

4.4.1 使用sklearn估计器构建线性回归模型

4.4.2 回归结果可视化

4.4.3 评价回归模型

第5章 航空公司客户价值分析

5.1 了解航空公司现状与客户价值分析

5.2 缺失值与异常值处理

5.3 选取并构建LRFMC模型的5个特征

5.4 使用K-Means算法进行客户分群

第6章 财政收入预测分析

6.1 了解财政收入预测的背景和方法

6.2 分析财政收入数据特征的相关性

6.3 使用Lasso回归选取财政收入预测的关键特征

6.4 计算相关系数非零的个数

6.5 使用SVR构建财政收入预测模型

所有评论(0)

Koonan-Edogawa

第4章使用scikit-learn构建模型

第5章航空公司客户价值分析

第6章财政收入预测分析