最小生成树

• 用途：用最少的资源构建起支撑这n个节点的一张网或图

1、概念

• 生成树（要求连通但是没有回路）
  
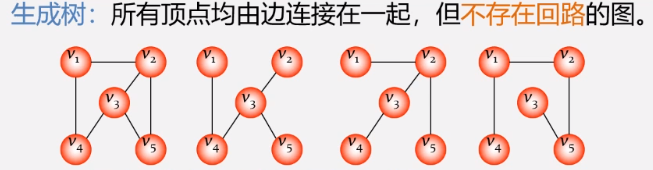
• 一个图可以有许多颗不同的生成树
• 所有生成树的共同特点：

1. 生成树的顶点个数与图的顶点个数相同
2. 生成树是图的极小连通子图，去掉一条边则非连通
3. 一个有n个顶点的连通图的生成树有n-1条边
4. 在生成树中再加一条边必然形成回路
5. 生成树中任意两个顶点间的路径是唯一的

• 含n个顶点n-1条边的图不一定是生成树

• 构造生成树的思路（以无向图的生成树为例）

1. 利用深度优先遍历搜索得到
   
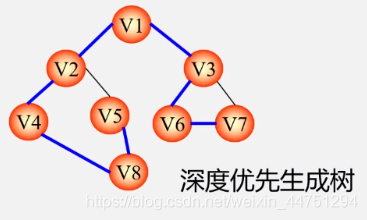
2. 利用广度优先遍历搜索得到
   
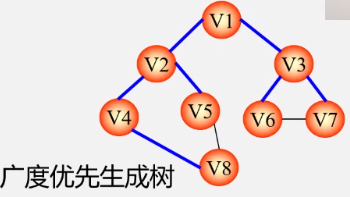
3. 总结
   

• 定义
  
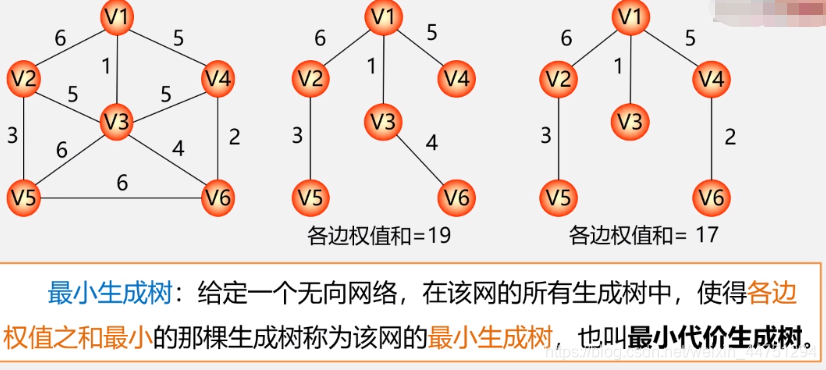
• 应用
  （n个城市最少就是n-1条路，确保连通，最多有C_n²条路）
  

2、MST概念

• MST性质：
  

• MST性质例子：
  
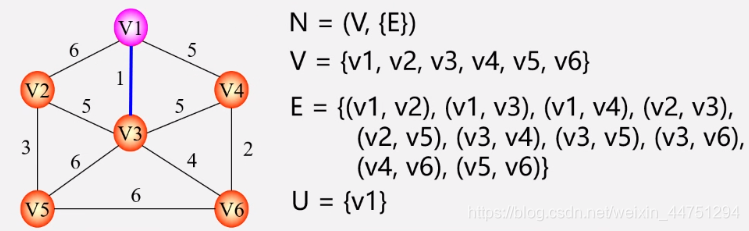
    此时，u是顶点集v的非空子集，再V-U集合就是差集。其中，以v1为例，其和v2,v3,v4都有一条边，其中v1到v3边的权值最小，根据MST性质，就是说其一定会包含在某一颗最小生成树中。

• MST性质解释
  
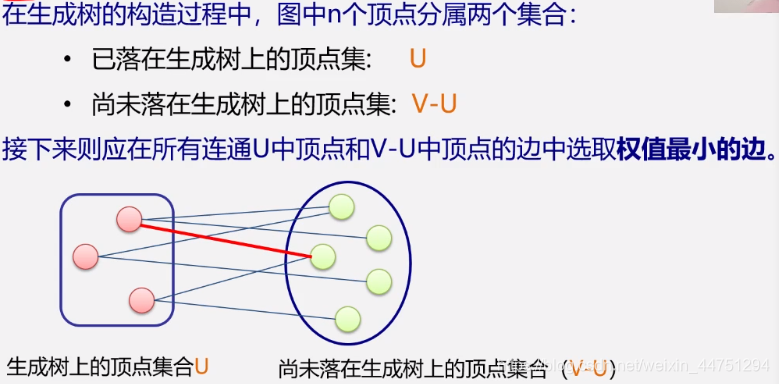
  ps：如果加上了这条边会造成回路，再忽略再选取其他权值最小的边。

3、实现

• 构造最小生成树方法一：普里姆算法（Prim算法）
  
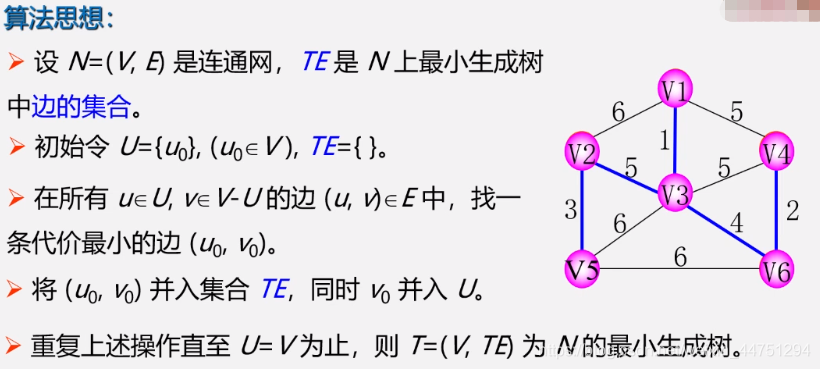
• 过程：

1. 假设一开始v1在u集合中，而u集合此时与差集只有v1-v2/v3/v43条边，选出其中权值最短的边v1-v3，权值是1，再将v3加入u集合。
2. 此时，u集合中有v1，v3两个顶点，这两个顶点与其他的顶点间权值最小的边是v3-v6，权值是4，然后将v6也加入u集合。
3. 此时，u集合中有v1，v3，v6，此时与其他顶点最短的边是v6-v4，权值是2的边，所以将v4也加入u集合。
4. 此时，u集合中有v1，v3，v4，v6，此时与其他顶点最短的边是v3-v2，权值是5，然后将v2也加入u集合。
5. 此时，u集合中离v5最短的边是v2-v5，将最后的v5加入u集合，结束，此时所选的边加上顶点就是最小生成树。

• 构造最小生成树方法二：克鲁斯卡尔（Kruskal算法）
  （将权值最小的边由小到大排序，不断的选取权值最小的边，前提是不能形成环）
  
  （最小生成树不唯一）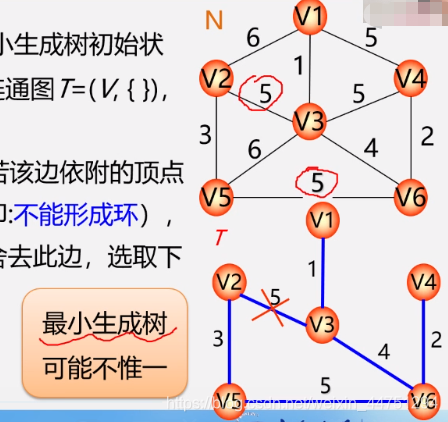
  
• 两种算法的比较
  
  （提示：由于Kruscal算法是按边来操作，而稀疏图的边比较少，所以适合稀疏图）

最短路径

• 用途：求两点间最短路径或某源点到其他各点最短路径

1、概念

• 问题：
  

• 第一类问题：两点间最短路径
  
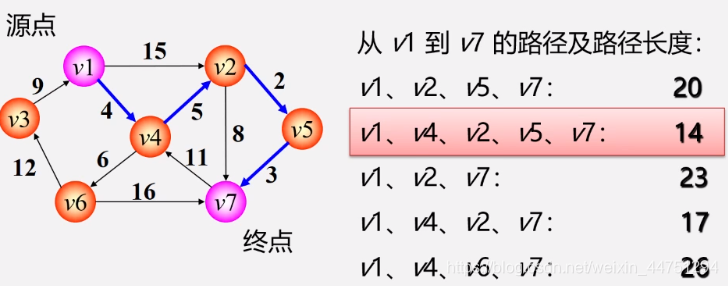
  可见，第二条路径最短最优

• 第二类问题：某源点到其他各点最短路径
  

• 实现的算法：
  

2、实现

Dijkstra(迪杰斯特拉)算法

• 单源最短路径 — Dijkstra(迪杰斯特拉)算法
  

• 实现思路：按路径长度递增次序产生最短路径
  

• 例子
  

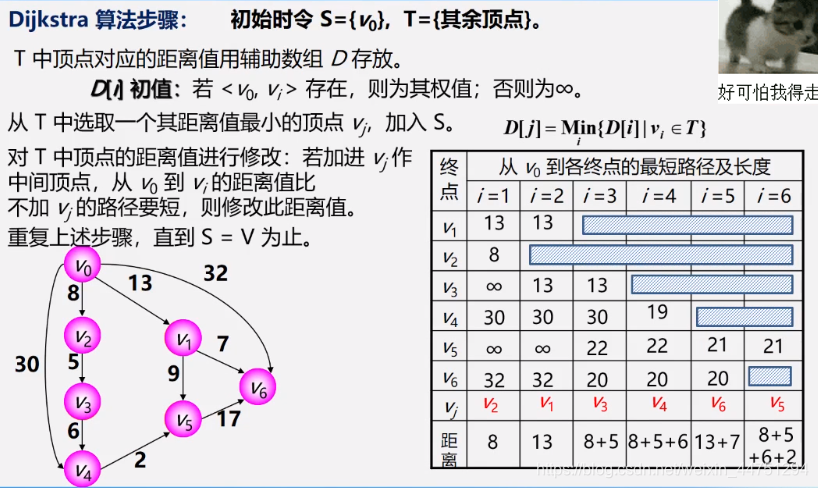
• 分析：

1. 一开始的S集合中只有v0，此时v0里其他顶点的距离如图所示，其中到达不了的设为无穷大。其中v0到v2的距离最短，为8，所以选取v2加入S集合，此后就不需要再对比到v2的距离。
2. 此时S的集合中有V0，v2，再次看看有了V2顶点的加入，能不能剪短到其他顶点的距离。可见，有了v2的加入，v0可以到达v3，距离为13，最短的距离，但是v0到v1也是最短的距离。所以这一次选取v1加入S集合，此后不需要再对比v1的距离。
3. 此时S的集合中有v0，v1，v2，再次看看有了v1顶点的加入，能不能剪短到其他顶点的距离。可见，有了v1的加入，v0又可以到达v5，v6，但是这次的最短距离是上次的v2到v3，所以选取v3加入S集合，此后不再需要对比v3的距离
4. 此时S的集合中有v0，v1，v2，v3，再次看看有了v3顶点的加入，能不能剪短到其他顶点的距离。可见，有了v3的加入，v0又可以到达v4，切这次到达v4的距离更短，为19，比此时其他的距离都短。所以选取v4加入S集合，此后不再需要对比v4的距离.
5. 此时S的集合中有v0，v1，v2，v3，v4，再次看看有了v4顶点的加入，能不能剪短到其他顶点的距离。可见，有了v4的加入，v0又可以到达v5，且这次到达v5的距离更短，为21，但是v0到v6的距离更短。所以选取v6加入S集合，此后不再需要对比v6的距离.
6. 最后一次，选取v5加入S集合，此时全部的顶点都加入了S集合，算法结束。

弗洛伊德（Floyd）算法

• 所有顶点间的最短路径

1. 方法一：每次以一个顶点为源点，重复执行Dijkstra算法n次。
2. 方法二：弗洛伊德（Floyd）算法

• 算法思路
  
• 例子：
  
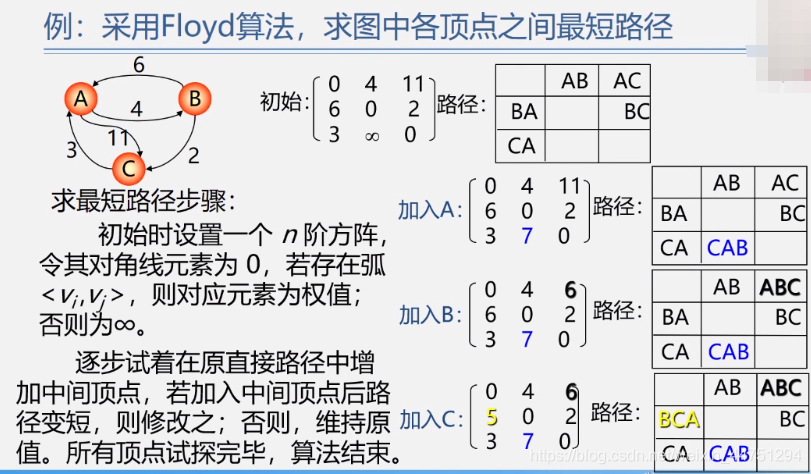
• 分析：

1. 本来的路径长度如图所示。
2. 加入了A顶点之后，本案例C是不能到达B的，所有距离是无穷大，但是增加了A顶点之后，C可以到达B，距离为3+4=7，所以表格的距离修改为7.
3. 加入了B顶点之后，本来A去C只能是11，但是现在可以借住B来到达C，距离更短，为6.
4. 加入了C顶点之后，本来B去A需要6个距离，现在借助C，2+3=5，距离更短。
5. 算法结束，此时就得到了有向网中的所以顶点的最短路径。经过的顶点和路径权值如最后的表所示。

拓扑排序

• 用途判断AOE网中是否存在环。

1、概念

• 有向无环图：无环的有向图，简称DAG图
  

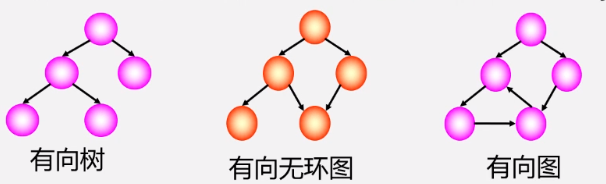
• 用途
  

• AOV网与AOE网
  
  ps：通常AOV网用来解决拓扑排序问题，而AOE网用来解决关键路径问题。

• AOV网的特点
  

• 其中：

1. C1是C4的直接前驱，C4是C1的直接后继
2. C1是C5的前驱，C5是C1的后继

问题：如何判断AOV网中是否存在回路？ ---- 拓扑排序

• 拓扑排序的定义
  

2、拓扑排序的方法

• 例子：过程如下所示（拓扑序列不唯一）
  
  
  
  
  
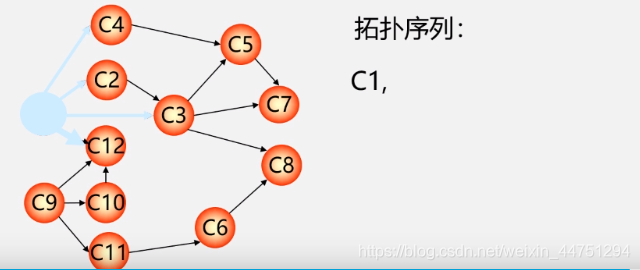
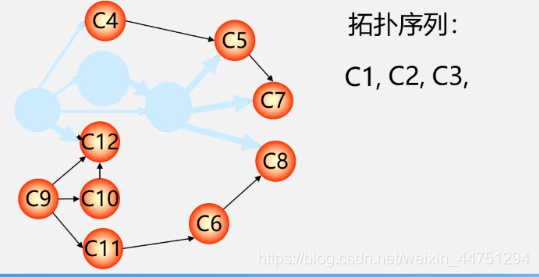
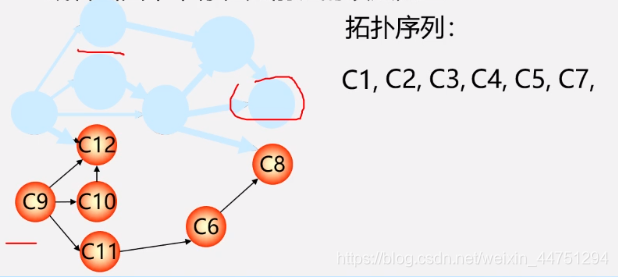
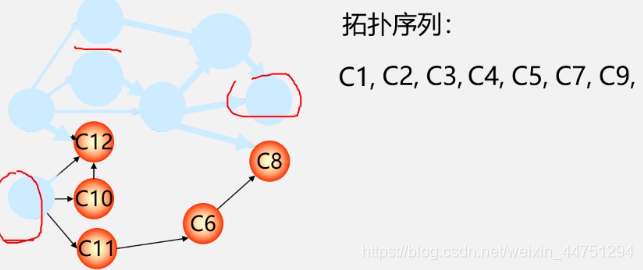
  不唯一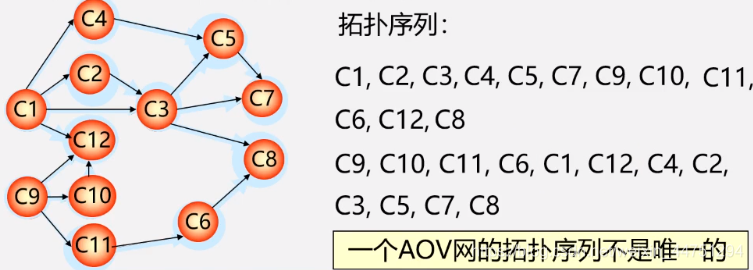
  
• 检测AOV网中是否存在环的方法：
  
  否则互相存在前驱必有环。

关键路径

• 引子
  

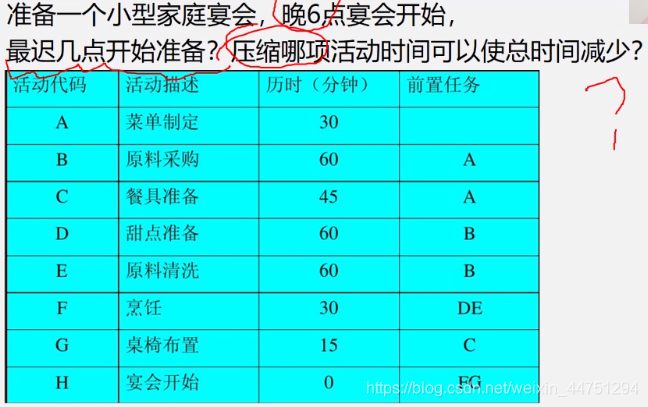
• 建模（AOE网的抽象）
  
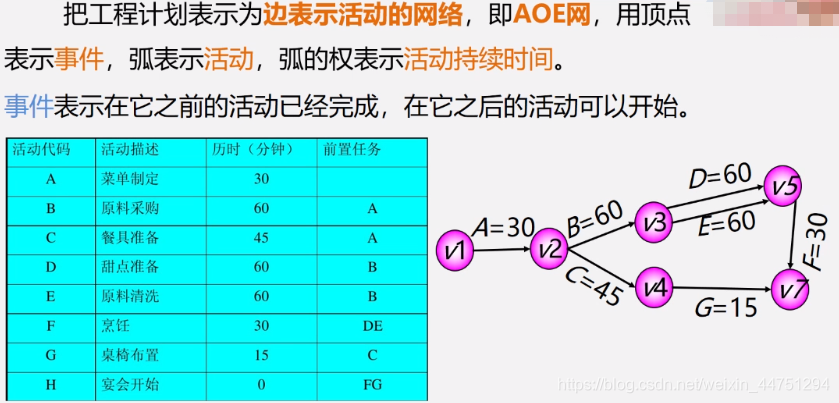
  解析：其中的v1->v2，表示菜单定制活动开始，到v2菜单定制活动结束，花费的时间A=20分钟。其他同理。

• 建模二
  
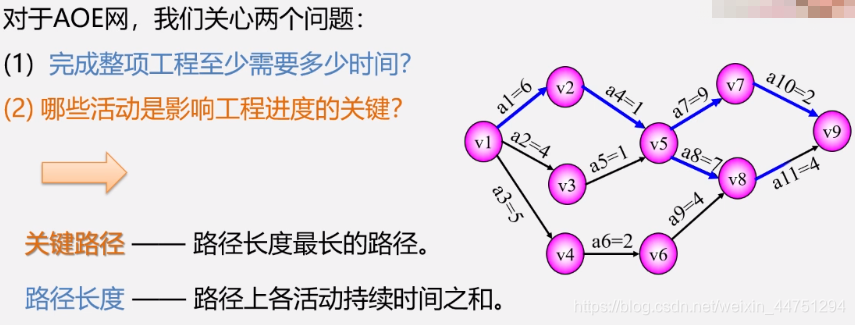
  将问题转化为求解关键路径问题–根据AOE网求解关键路径

• 关键路径所需的一些描述量
  

• 描述量的求解方法
  

• 最早发生时间求解例子 – 正在算
  
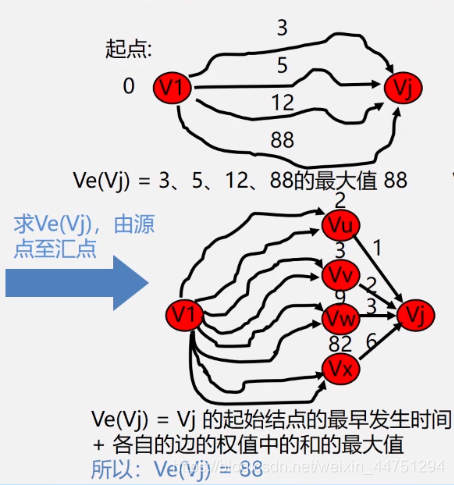
  解析：尽管v1只需2天的时间就到了Vu活到开始，再过1天时间就可以结束。但是v1到Vx要长达82天的时间，而之后还有进行6天才能结束，所以要提前82+6天才能确保活到完成，这个时间也就是最早发生时间。

• 最晚发生时间求解例子 – 逆着算
  

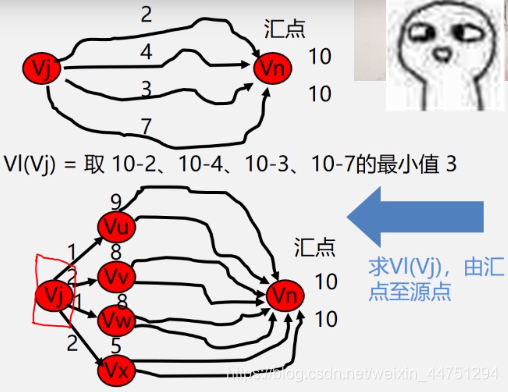
• 示例
  
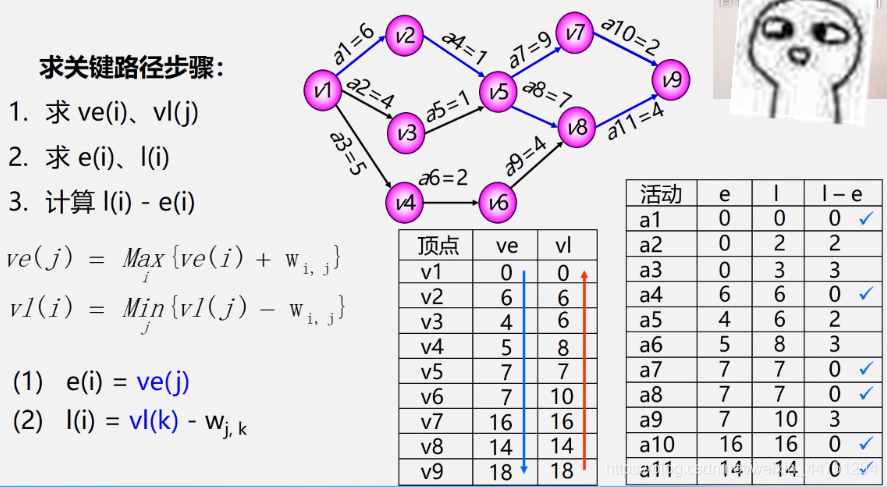
  如图所示：
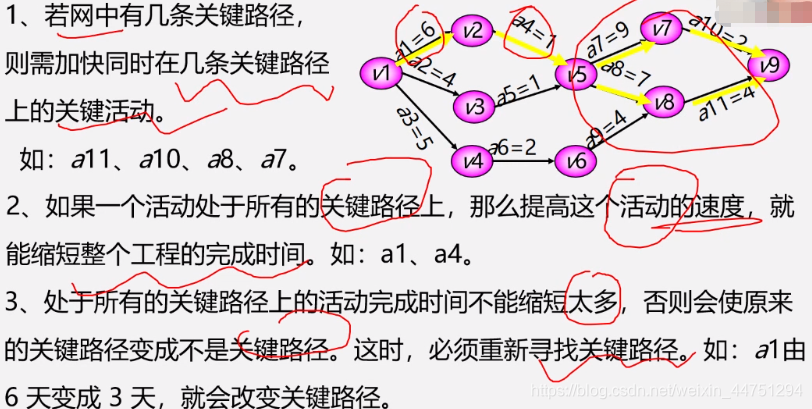
  时间余量为0的活动就是关键活动，由关键活动组成的路径就是关键路径。

• 总结
  

参考链接：王老师的教学视频