》》》算法竞赛

/**
 * @file            
 * @author          jUicE_g2R(qq:3406291309)————彬(bin-必应)
 *						一个某双流一大学通信与信息专业大二在读	
 * 
 * @brief           一直在算法竞赛学习的路上
 * 
 * @copyright       2023.9
 * @COPYRIGHT			 原创技术笔记：转载需获得博主本人同意，且需标明转载源
 *
 * @language        C++
 * @Version         1.0还在学习中  
 */

• UpData Log👆 2023.9.4 更新进行中
• Statement0🥇 一起进步
• Statement1💯

技术提升站点

高级数据结构

14 并查集

主要用于处理一些不相交集合的合并问题

经典的应用：连通图，最小生成树 Kruskal 算法，最近公共祖先LCA算法

14-1 基本操作

how many tables(HDU 1213)

要求

有 n 个人一起吃饭，互相认识的坐在同一个桌子：A认识B，B认识C，三人坐在同一张桌子

INPUT

第一行输入有几个测试 tst

第二行输入有 n 个人参加该测试，他们之间有 m 个关系（1<= n, m <= 1000）

接下来 m 行输入关系

1
10 7
1 2
2 3
4 5
5 6
7 8
9 10
10 6

容易看出来：

1 2 3

4 5 6 9 10

7 8

OUTPUT

输出桌子的个数（即集的个数）

3

一个桌子就是一个集，合并他们的朋友关系

//Merge_Set     集的合并
#include<bits/stdc++.h>
using namespace std;
const int MAX=1050;
vector<int> s(MAX);
int FindSet(int p){                     //查找
    return s[p]==p ? p:FindSet(p);      //s[p]==p不成立的话继续递归直到查到为止（实质就是DFS）
}
void MergeSet(int p1,int p2){            //合并集
    p1=FindSet(p1);     p2=FindSet(p2);
    if(p1!=p2)           s[p1]=s[p2];
}
int main(void){
    int t,n,m,x,y;              cin>>t;
    while(t--){
        cin>> n >> m;
        for(int i=1;i<=MAX;i++)         //初始化所有集
            s[i]=i;                     
        for(int i=1;i<=m;i++){    
            cin>> x >> y;
            MergeSet(x,y);
        }
        int ans=0;
        for(int i=1;i<=n;i++)
            if(s[i]==i)  
                ans++;
        cout<<ans<<endl;
    }
    return 0;
}

14-2 合并的优化

为何需要优化？

FindSet 与 MergeSet的搜索深度是树的高度，极端情况下复杂度都为O(n)

利用并查集的合并和查询优化，使 O(n) 优化到小于 O(log₂n) ，约为O(1)

vector<int> h(MAX,0);					//树的高度
void MergeSet(int p1,int p2){
    p1=FindSet(p1);     p2=FindSet(p2);
	//下面对合并操作进行了优化
    if(h[p1]==h[p2]){
        s[p2]=x;						//p2的根节点（即集）并到p1上
        h[p1]++;						//树增高
    }
    else{								//矮树并到高树上，树高不变
        if(h[p1]>h[p2])			s[p2]=p1;	
        else			 	    s[p1]=p2;
    }
}

注

一般无需合并的优化，因为在路径压缩时，附带有优化合并的作用

14-3 路径压缩（查询的优化）

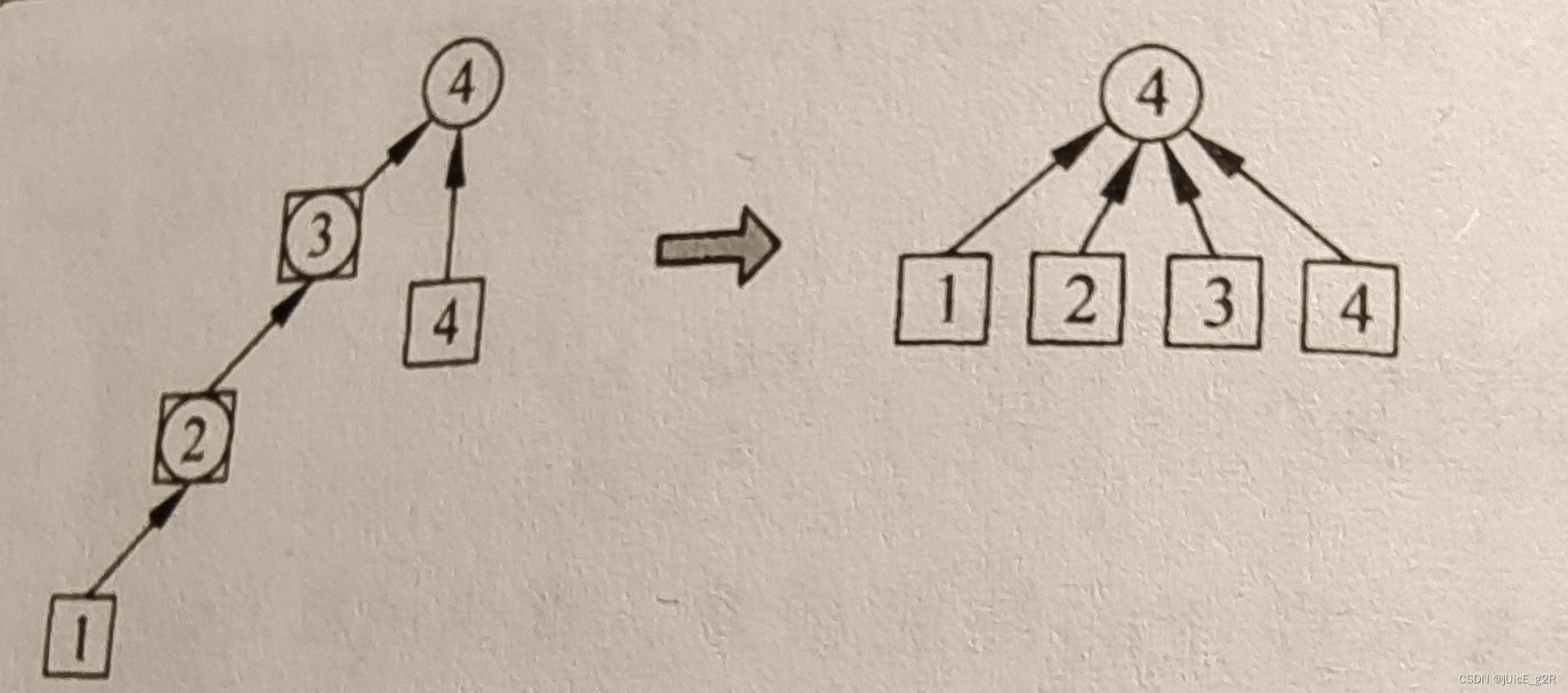
为何需要优化？

FindSet中，查询元素 i 的所属的集需要搜索路径找到根节点，返回根节点，这段路径可能会很长，每次搜索都需要重复该操作会很费时

在返回根节点的同时将 i 所属的集改为根节点即可节省后续搜索的时间（其实就是将 DFS 转为 BFS）

//原来DFS递归后只是单纯的直接返回根节点
int FindSet(int p){                     		//查找
    return s[p]!=p ? FindSet(p):p;      		//s[p]==p不成立的话继续递归直到查到为止（实质就是DFS）
}
//修改后
int FindSet(int p){
    if(s[p]!=p)		s[p]=FindSet(s[p]);			//将 i 所属的集改为根节点
    return s[p];							   //返回根节点
}

解决潜在的爆栈问题

上述递归过程，数据规模太大会引发爆栈问题，改为 非递归

int FindSet(int p){
    int root=p;
    while(s[root]!=root)	
        root=s[root];						//查找到根节点
    while(p!=root){
        int temp=s[p];
        s[p]=root;
        p=temp;
    }
    return root;
}

14-4 带权并查集

并查集和树这种数据结构很相似，并查集其实就是在维护若干棵树。

并查集的合并与查询优化，实际是在改变树的形状，把原来"细长的、操作低效的、大量的"小树，变为”粗短的、操作高效的、少量的“大树。

• 带权值的路径压缩（查询部分代码）

vector<int> w(MAX,0);					//权值
int FindSet(int p){
    if(p!=s[p]){
        int parent=s[p];				//父节点
        s[p]=FindSet(s[p]);				//路径压缩，递归返回根节点
        w[p]+=w[parent];				//最终将 p到root 路径上的权值全部加在根节点上
    }
    return s[p];						//返回根节点
}

如何理解带权并查集

部分转载源https://blog.csdn.net/hnjzsyjyj/article/details/120211514

带权并查集的核心能力就是维护多个元素之间的连通以及偏移关系，甚至可以维护多个偏移关系。而偏移量可以理解为当前结点到根结点的距离之和。其核心运算是向量运算。

• 思路

设roota是a的根结点，rootb是b的根结点，v是a->b的关系值，val[x]是某结点x到其根结点的关系值（如距离）

1、当roota ！= rootb时：

由上图可知，如果将 roota 归附于 rootb，那么依据向量运算规则（注：这里的 ‘->’ 不是指针，写的只是纯粹的数学式）可推出 roota->rootb = (a->b) + (b->rootb) - (a->roota)

由于 dis [x] 数组 存储的是某结点x到其根结点的距离，而 roota 的根节点是 rootb ，所以有等价表示 roota->rootb = dis[roota] 。相应的，有 b->rootb = dis[b]、a->roota = dis[a] ，则式子 roota->rootb = (a->b) + (b->rootb) - (a->roota) 可表示为：dis[roota] = v + dis[b] - dis[a]。

2、当roota == rootb时：

由上图可知， a和b的根结点相同。所以我们只需验证 a->b 是否与题目中给定的值一致。显然，依据向量运算规则可推出 a->b = (a->root) - (b->root)，等价表示为 v = dis[a] - dis[b]。

显然，依据向量运算规则可推出 a->b = (a->root) - (b->root)，等价表示为 v = dis[a] - dis[b]。

下面的代码都会参照上述的向量运算法则！！！

How many answers are wrong(HDU 3038)

要求

给出 区间[a,b] ，区间和为sum，输入m组数据，每输入一组，判断此组条件是否与前面冲突，最后输出与前面冲突的数据个数

例如给出 区间1：[1,5] ，区间和为100，区间2：[1,2]，区间和为200，两者间一定是有冲突的

INPUT

第一行 输入n（有n个数，<=200000），m（有 m 组数据,<=40000）

后面 m 行，每行输入 a,b,v

10 5
1 10 100
7 10 28
1 3 32
4 6 41
6 6 1

OUTPUT

输出冲突数据的个数

1

注意

由于问题HDU 3038使用的都是闭区间，闭区间会加上端点的值，这就提醒我们这个题在处理的时候应该将闭区间的某一端变成开区间，比如将[1,4]变成(0,4]，将[3,4]变成(2,4]，将[1,2]变成(0,2]等，即左开右闭。

• 代码展示

#include<bits/stdc++.h>
using namespace std;
using LL=long long int;
const int MAX=200010;
vector<int> s(MAX);                     //集
vector<LL> w(MAX,0);					//权值
int clash=0;                            //冲突
int FindSet(int p){
    if(p!=s[p]){
        int parent=s[p];				//父节点
        s[p]=FindSet(s[p]);				//路径压缩，递归返回根节点
        w[p]+=w[parent];				//最终将 p到root 路径上的权值全部加在根节点上
    }
    return s[p];						//返回根节点
}
void MergeSet(int p1,int p2,LL v){    //向量运算规则
    int root1=FindSet(p1);      int root2=FindSet(p2);
    if(root1==root2){                   //如果条件成立的话根据向量规则应该有下面条件成立，否则就产生了冲突
        if(w[p1]-w[p2]!=v)
            clash++;
    }
    else{
        s[root1]=root2;                 //root1集合并到root2上
        w[root1]=w[root2]-w[root1]+v;
    }
}
int main(void){
    int n,m;
    while(scanf("%d %d",&n,&m) != EOF){
        for(int i=0;i<=MAX;i++)             //集的初始化
            s[i]=i;                         
        while(m--){
            int a,b;    LL v;
            scanf("%d %d %lld",&a,&b,&v);
            a--;                            //左开右闭，前移一位左边值
            MergeSet(a,b,v);
        }
    }
    cout<<clash;
    return 0;
}