典型的：HTML 就是一个树结构

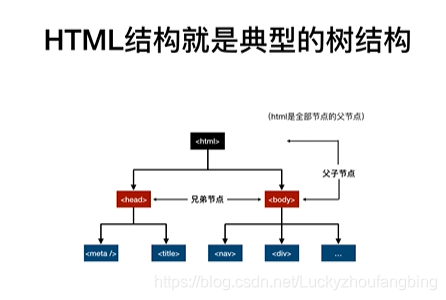
（一）二叉树

特点：

1. 每一个父结点都有两个子结点

2. 左侧子节点存储比父结点小的值，右侧子节点存储比父结点大的值

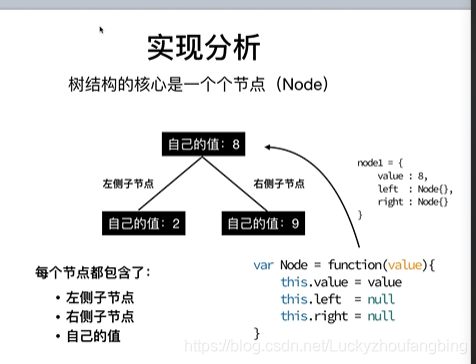
操作：增删改查

代码：

// 定义Node节点
    class Node {
      constructor (value) {
        this.value = value,
        this.left = null,
        this.right = null
      }
    }

    class Tree {
      constructor () {
        this.root = null // 首先定义根节点 为null
      }

      // 寻找插入节点
      insertNode (node, CurrentNode){
        if (node.value > CurrentNode.value) {
          if (CurrentNode.right) {
            this.insertNode(node, CurrentNode.right) // 递归 继续向下寻找
          } else {
            CurrentNode.right = node
          }
        } else if (node.value < CurrentNode.value) {
          if (CurrentNode.left) {
            this.insertNode(node, CurrentNode.left) // 递归 继续向下寻找
          } else {
            CurrentNode.left = node
          }
        }
      }
      // 插入
      insert (value) {
        var node = new Node(value)
        if (this.root) {
          this.insertNode(node, this.root)
          // 因为要递归 所以 单独封装方法
        } else {
          this.root  = node // 没有根节点 设置为根节点
        }
      }

      // 遍历节点
      traverse (callback) {
        this.traver(this.root, callback)
      }

      traver(node, callback) {
        if (node === null) {
          return
        }
        this.traver(node.left, callback)
        callback(node.value) // 中序遍历 后序遍历 前序遍历等等高改变这行代码位置
        this.traver(node.right, callback)
      }

      // 删除节点
      remove () {

      }

      // 二叉树最小值 找到最左节点
      getMin () {
        // 空树返回null
        if (this.root === null) {
          return null
        }
        var current = this.root
        while(current.left) {
          current = current.left
        }
        return current.value
      }

      // 获取二叉树搜索树最大值 最右节点
      getMax () {
        // 空树返回null
        if (this.root === null) {
          return null
        }
        var current = this.root
        while(current.right) {
          current = current.right
        }
        return current.value
      }

      // 获取树
      getTree () {
        return this.root
      }
    }
    var tree = new Tree()
    tree.insert(12)
    tree.insert(13)
    tree.insert(4)
    tree.insert(13)
    console.log(tree.getTree())
    tree.traverse((value) => {
      console.log('VALUE', value)
    })
    console.log(tree.getMin())
    console.log(tree.getMax())

还有删除一个结点，情况复杂 单独贴

移除一个结点 三种情况：

1. 该结点没有子节点 直接移除就可以

2. 该结点有一个子结点，将子结点替换为该结点

3. 该结点有两个子结点，这种情况最特殊 需要重新计算（最好的方案，一句话总结：替换为右侧子树的最小子结点）

一个结点，它左侧的树的所有值都比它小，它右侧的所有值都比他大，比它小才能往左侧走，比它大才能往右侧去

// 删除结点 先查找 再删除
      removeNode (node, value) {
        if (node === null) { return null }
        if (value < node.value) { // 左侧找
          node.left = this.removeNode(node.left, value)
          return node
        } else if (value > node.value) { // 右侧找
          node.right = this.removeNode(node.right, value)
          return node
        } else { // 值相等 找到 node 就是当前结点
          if (node.left === null && node.right === null) {  // 叶结点 没有子结点 直接删除 反向构建 一层层 return
            node = null
            return node
          }
          if (node.left === null && node.right) {
            node = node.right
            return node // 右结点替换
          }
          if (node.right === null && node.left) {
            node = node.left
            return node // 左结点替换
          }
          if (node.right && node.left) { // 左右结点都存在
            var minNode = this.findMinRight(node.right)
            node.value = minNode.value
            node.right = this.removeNode(node.right, node.value) // 从替换元素查找 删除value的元素
            return node
          }
        }
      }

      // 查找传入结点的最小子结点
      findMinRight (node) {
        if (node === null) {
          return null
        }
        while (node.left) {
          node = node.left
        }
        return node
      }
      // 删除节点 重新构建树
      remove (value) {
        this.root = this.removeNode(this.root, value)
      }

慢慢研究 一环套一环。。。头秃