面试复习——数据结构(五):串
数据结构复习(五):串
文章目录
串
串的基本概念
串的定义
串(即字符串,string)是由零个或多个字符组成的有限序列,是一类特殊的线性表。
BUT,串的基本操作和线性表有很大差别,通常以“串的整体”作为操作对象:在串中查找子串、插入子串、删除子串、替换子串。
s = " a 1 a 2 a 3 . . . a n " , n > = 0 s = "a_1a_2a_3...a_n", n>=0 s="a1a2a3...an",n>=0 (隐含结束符 ‘\0’)
特殊的串:
空串 null string: s = “ " s=“" s=“" 长度为0
空格串 blank string: s = “ s=“ s=“ " " " 长度为2
子串
子串是串中任意个连续的字符组成的子序列
主串
主串是包含子串的串
子串在主串中的位置是以子串的第一个字符在主串中的位置来表示的
PS:空串是任意串的子串,任意串是其自身的子串
真(proper)子串:除串本身以外的子串都称为真子串。
平凡(trivial)子串:非空且不同于串本身的子串
串的前缀
串的前缀是串中最靠前的若干个字符
串的后缀
串的后缀是串中最靠后的若干个字符
PS:空串是任何串的前缀、后缀,任意串是其自身的前缀、后缀
平凡前缀,平凡后缀,真前缀,真后缀
串的相等
两个串相等当且仅当这两个串的值相等,即,两个串的长度相等,且对应位置的字符均相同
字符相等意味着字符所对应的ASCII值相等
C语言中的串处理函数
用字符数组存放串
C语言<string.h>中的串处理函数
| 函数名 | 功能 |
|---|---|
| char *gets(char *str) | 从stdin中读取串 |
| int puts(char *str) | 向stdout输出串 |
| int strlen(char *str) | 返回串的长度 |
| char *strcpy(char *dest, char *src) | 复制串 |
| char *strcat(char *dest, char *src) | 联接串 |
| int strcmp(char *str1, char *str2) | 比较串, s1<s2时返回负数,相等返回0,s1>s2时返回正数 |
| char *strstr(char *str,char *substr) | 返回子串首次出现的位置 |
| strchr | 检索并返回字符c在字符串s中第一次出现的位置 |
| strrchr | 检索并返回字符串s中最后一次出现给定字符c的位置 |
| strspn | 检索并返回在s1和s2中均有的字符个数 |
| strpbrk | 检索并返回两个字符串中首个相同字符的位置 |
| strupr | 将字符串s中的小写字母全部转换成大写字母,并返回转换后的字符串 |
| strlwr | 将字符串s中的大写字母全部转换成小写字母,并返回转换后的字符串 |
| strtol | 将字符串str转换成长整型数,并返回这个数 |
| strtod | 将字符串str转换成双精度数,并返回这个数 |
| strdup | 将字符串s复制到新建的位置 |
| strrev | 将字符串逆置 |
| strtok | 将字符串分割成由定界符隔离的一个个片段 |
| strncat | 将字符串src中最多maxlen个字符复制到字符串dest中 |
| strncmp | 比较字符串s1与s2中的前maxlen个字符 |
| strncpy | 复制src中的前maxlen个字符到dest中 |
| stricmp | 以不区分大小写的方式比较字符串s1和s2,并返回s1-s2 |
| strnicmp | 以不区分大小写的方式比较字符串s1与s2中的前maxlen个字符 |
串的操作
基本操作
- 加工型
初始化串StrInit
销毁串StrDestry
清空串StrClear
串赋值StrAssign
串联接StrConcat
取子串StrSubstr - 引用型
求串长StrLen
判串等IsStrEqual
串比较StrComp
其他操作
- 加工型
串插入StrInsert
串删除 StrDelete
串复制StrCopy
串替换StrReplace - 引用型
判是否空串IsStrEmpty
串查找/串匹配StrIndex
串的具体实现
顺序串/定长顺序存储
定长顺序存储表示:用一组地址连续的存储单元存储串值的字符序列,属静态存储方式
#define MAXSTRLEN 255
Typedef unsigned char SString[MAXSTRLEN+1];
// !这里定义首字符存放串长度
// 串拼接
int StrConcat(SString t,SString s1,SString s2){
int uncut;
if (s1[0]+s2[0] <= MAXSTRLEN) {
strncpy(&t[1],&s1[1],s1[0]);
strncpy(&t[s1[0]+1],&s2[1],s2[0]);
t[0]=s1[0]+s2[0];t[t[0]+1]='\0';
uncut= 1;
}else if(s1[0]<MAXSTRLEN) {// s2被截断
strncpy(&t[1],&s1[1],s1[0]);
strncpy(&t[s1[0]+1],&s2[1], MAXSTRLEN-s1[0]);
t[0]=MAXSTRLEN;t[MAXSTRLEN+1]='\0'; uncut=0;
}else {
//s1[0] >= MAXSTRLEN,故s2被截断,仅取s1
strncpy(&t[1],&s1[1],MAXSTRLEN);
t[0]=MAXSTRLEN;t[MAXSTRLEN+1]='\0';
uncut=0;
}
return uncut;
}
//取子串,将s中从第pos个字符开始的连续len个字符放到sub中
bool StrSubStr(SString sub, SString s,int pos, int len) {
if(pos<1 || pos>s[0] || len <0 || len > s[0]-pos+1) return false;
strncpy(&sub[1],&s[pos],len);
sub[0]= len; sub[sub[0]+1]='\0';
return true;
}
一个比较经典的问题:串匹配
在主串s的第pos个字符之后寻找与t相等的子串,找到则返回第一个这样的子串在S中的位置,否则返回0
思路一:暴力求解算法
将主串s的第pos个字符和模式t的第1个字符比较
→ 若相等,继续逐个比较后续字符;
→ 若不等,则从主串s的(pos+1)字符起,重新与t第1个字符比较。
直到主串s的一个连续子串字符序列与模式t相等。返回值为s中与t匹配的子序列第一个字符的序号,即匹配成功,否则,匹配失败,返回值 0。
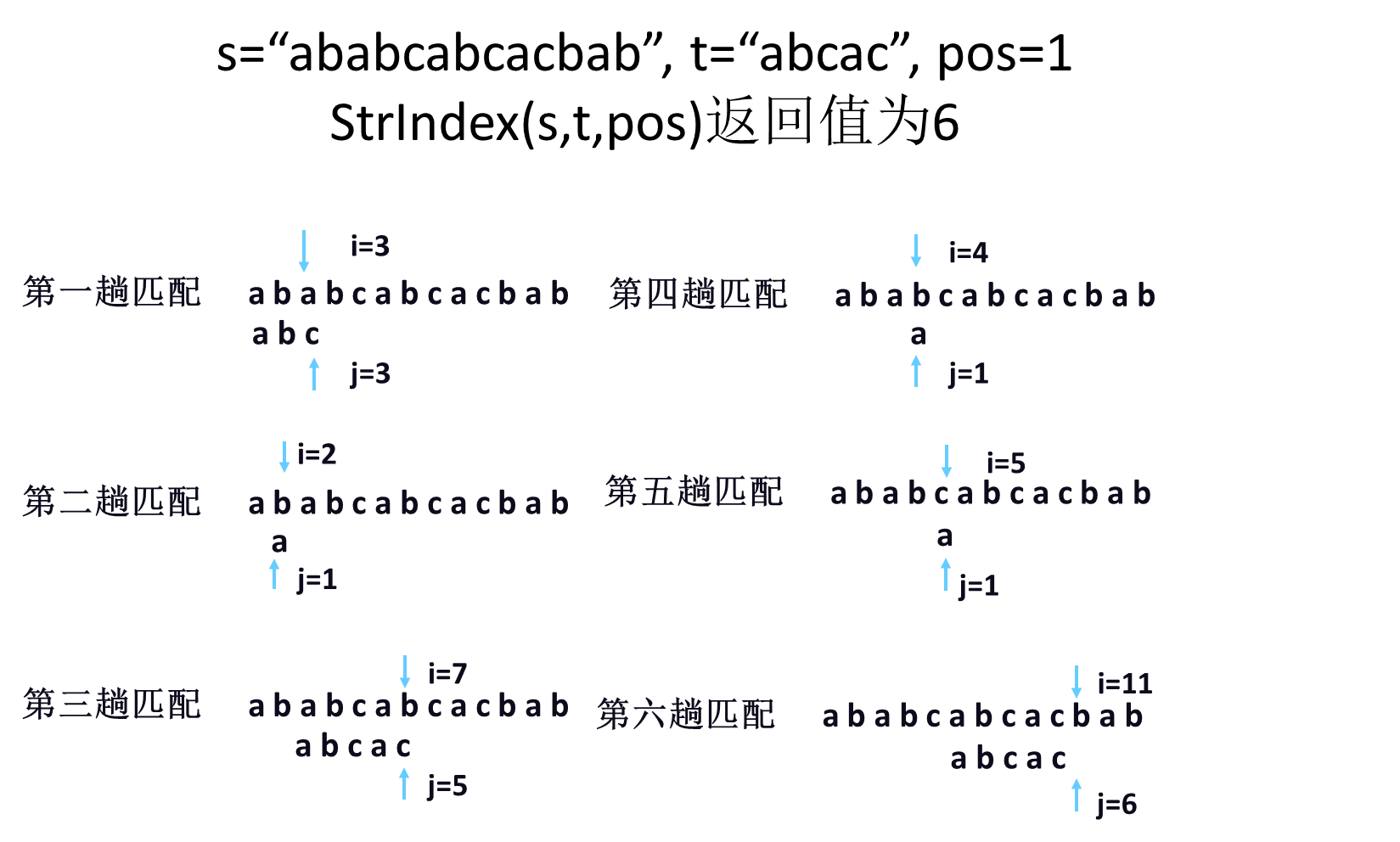
int StrIndex(SString s,SString t,int pos){
int i,j; i=pos;j=1;
while(i<=s[0] && j<=t[0]){
if(s[i] == t[j]) {i++;j++;} //继续比较后继字符
else {i=i-j+2;j=1;}
//指针i后退(至当前匹配起始位置的下一位置)
}
if(j>t[0])
return i-t[0]; //匹配成功,返回子串t的位置
else return 0;
}
复杂度:
令主串s的长度n,模式串t的长度m
最好情况:只经过一轮比对,即可确定匹配,匹配次数 = m = O(m)
最坏情况:每轮都比对到模式串的最后一个字符
- 每轮循环,匹配次数 = m (前m-1次匹配,成功;最后一次失败)
- 循环次数,n-m+1
- 一般有m << n,所以,总的匹配次数=m * (n-m+1) =O(n*m)
顺序串/堆分配存储
堆分配顺序存储表示:用一组地址连续的存储单元存储串值的字符序列,但存储空间是在程序执行过程中动态分配而得到的(堆:自由存储区,用C语言的动态分配函数从中获得可用的存储空间)
ADT定义:
#define INITSTRLEN 255
typedef struct {
char *ch; //若是非空串,则按串长度+1分配存储区
int length; //串长
int strsize; //存储空间大小,包含串的结束符
} HString;
// 1.初始化串
bool StrInit (HString *s);
// 2. 获取串的长度
int StrLen(HString *s);
// 3. 比较两个串是否相等
bool IsStrEqual(HString *s,HString *t);
// 4. 比较两个串
Int StrComp(HString *s,HString *t);
//5. 将字符串常量sc赋给字符串变量s
bool StrAssign (HString *s,char *sc);
//6. 将s1和 s2拼接成s
bool StrConcat (HString *s,HString *s1, HString *s2);
//7. 取子串,将s中从第i个字符开始的连续j个字符放到subs
bool StrSubstr(HString *subs, HString *s,int i,int j);
//8. 在s的第i个字符之前插入字符串t
bool StrInsert (HString *s,int i,HString *t);
//9. 删除s的第i个字符开始的连续j个字符
bool StrDelete(HString *s,int i,int j);
//10. 串替换,将s从第i个字符开始j个连续字符用字符串t替换
bool StrReplace (HString *s,int i,int j,HString *t);
//11. 将字符串变量的值赋给字符串变量s
bool StrCopy(HString *s,HString *t);
bool StrInit(HString *s){
s->ch = (char *)malloc(INITSTRLEN *sizeof(char));
if(!s->ch) return false;
s->ch[0]='\0';
s->length = 0;
s->strsize= INITSTRLEN;
return true;
}
int StrLen(HString *s){
return s->length;
}
bool IsStrEqual(HString *s1,HString *s2){
int i=0;
for(i=0;i<s1->length && i< s2->length; i++)
if(s1->ch[i]!= s2->ch[i]) return false;
if (i<s1->length || i<s2->length)
return false;
else return true;
}
//s等于t,返回0;s大于t,返回值大于0;s小于t,返回值小于0
int StrComp(HString *s,HString *t){
for(i=0;i<s->length && i<t->length;i++)
if(s->ch[i] !=t->ch[i]) return (s->ch[i]-t->ch[i]);
return (s->length-t->length);
}
// 将字符串常量赋给字符串变量s
bool StrAssign(HString *s, char *sc){
int i=0;
//求sc的串长度i,串尾特征是sc[i]=‘\0’
while(sc[i]!=‘\0’) i++;
if(i>= s->strsize) {
s->ch =(char *)realloc(s->ch, (i+1)*sizeof(char));
if(!s->ch) return false;
s->strsize = i+1; }
s->length = i;
for(i=0;i<s->length;i++)
s->ch[i] = sc[i];
s->ch[i]=‘\0’; //显式地补上串结束标志
return true;
}
bool StrConcat(HString *s,HString *s1, HString *s2) {
// 将s1,s2拼接成s
int i;
if(s->strsize < (s1->length + s2->length)){
s->ch = (char *)realloc(s->ch, (s1->length+s2->length+1) * sizeof(char));
if(!s->ch) return false;
s->strsize = s1->length + s2->length+1;
}
i=0;
while(i<s1->length) {s->ch[i]=s1->ch[i]; i++;} //拷贝s1串
while(i<s1->length+s2->length) {
s->ch[i]=s2->ch[i-s1->length];
i++;
} //拷贝s2串
s->ch[i]='\0'; s->length = s1->length+s2->length;
return true;
}
// 取子串,将s中从第i个字符开始的连续j个字符放到subs
bool StrSubstr(HString *subs, HString *s, int i, int j){
int k;
if(i<=0 || i> s->length || j<0 || j > s->length -i +1)
return false;
if(subs->strsize < j) {
subs->ch =(char *) realloc(subs->ch,(j+1)*sizeof(char));
if(!subs->ch) return ERROR;
subs->strsize =j+1;
}
for(k=0;k<j;k++)
subs->ch[k] = s->ch[i-1+k];
subs->ch[j]='\0';
subs->length=j;
return true;
}
//在s的第i个字符之前(1<=i<=s->length+1)插入字符串t
bool StrInsert(HString *s,int i,HString *t) { int j;
if(i<=0 || i>s->length+1) return false; // 位置不合法出错
if(s->strsize < s->length + t->length){ //空间不够
s->ch = (char *)realloc(s->ch,(s->length+t->length+1)* sizeof(char));
if(!s->ch) return false;
s->strsize = s->length + t->length;
}
for(j=s->length-1;j>=i-1;j--) //字符后移,腾挪空间
s->ch[j+t->length] = s->ch[j];
for(j=0;j<t->length;j++) // 插入t
s->ch[i+j-1] = t->ch[j];
s->length += t->length;
return true;
}
//串替换,将s从第i个字符开始j个连续字符用字符串t替换
bool StrReplace(HString *s, int i, int j, HString *t){
int k;
if(i<=0 || i> s->length || j<=0 || j>s->length-i+1) return false;
if(j<t->length) {
if(s->length + t->length-j > s->strsize) {
s->ch =(char *) realloc(s->ch,(s->length+t->length-j+1)*sizeof(char));
if(!s->ch) return false;
s->strsize = s->length + t->length –j+1;
}
for(k=s->length; k>=i+j-1;k--) //向后移,挪空间
s->ch[k-j+t->length] = s->ch[k];
}
else for(k=i-1+j;k<s->length;k++) s->ch[k-j+t->length] = s->ch[k]; //向前移
s->length = s->length + t->length -j; s->ch[s->length+1]='\0';
for(k=0;k<t->length;k++)
s->ch[k+i-1] = t->ch[k];
return true;
}
一个比较经典的问题:串匹配
在主串s的第pos个字符之后寻找与t相等的子串,找到则返回第一个这样的子串在S中的位置,否则返回0
思路一:暴力求解算法
块链存储
串的块链存储表示:链式方式存储,方便插入和删除结点
- 方法1:链表结点的数据分量长度取1(个字符)

这里方法1的存储密度为 1/2 - 方法2:链表结点(数据域)大小取n(例如n=4)
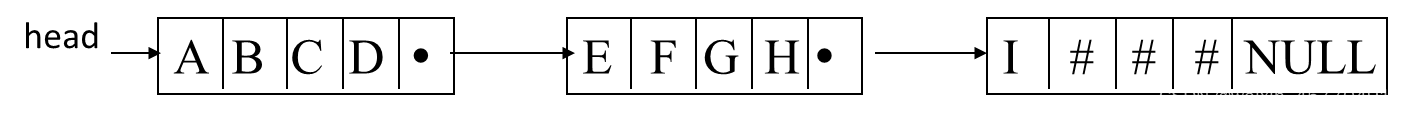
这里方法2的存储密度为 9/15 = 3/5
#define CHUNKSIZE 80 //每块大小,由用户定义
typedef struct Chunk { //首先定义结点类型
char ch[CHUNKSIZE];//每个结点中的数据域
struct Chunk * next ;//每个结点中的指针域
} Chunk;
typedef struct { //定义用链式存储的串类型
Chunk *head; //头指针
Chunk *tail; //尾指针
int curLen; //结点个数
} LString;
串的模式匹配
检测问题/Detection:检测模式串是否出现
定位问题/Location:首次在哪里出现
枚举问题/Enumeration:模式串分别出现在主串中的哪里
计数问题/Counting:模式串在主串中出现了几次
应用:
- 文本编辑器,编辑和格式化
Word,Tex,Latex - 正则表达式(Regular Expression):描述了一种字符串匹配的模式
- 心电图(ElectroCardioGraph,ECG)检测
串匹配问题
在主串s的第pos个字符之后寻找与t相等的子串,找到则返回第一个这样的子串在S中的位置,否则返回0
假设 S = “abcaabcaaabc”, T =“bca”,
Index(S, T, 1) = 2; Index(S, T, 3) = 6;
Index(S, T, 8) = 0;
思路一:暴力求解算法
将主串S的第pos个字符和模式串P的第1个字符比较
→ 若相等,继续逐个比较后续字符
→ 若不等,则从主串S的(pos+1)字符起,重新与P第1个字符比较
直到主串S的一个连续子串字符序列与模式串P相等。这时匹配成功,返回S中与P匹配的子序列第一个字符的序号,否则,匹配失败,返回值 0。
// 上面有用静态顺序串实现的方式
// 这里用的是顺序串堆实现的方式
int StrIndex(HString *s,HString *t, int pos){
int i,m,n;
HString sub; StrInit (&sub);
if(pos > 0) {
i=pos;n=StrLen(s);m=StrLen(t);
while(i<=n-m+1) {
StrSubstr(&sub,s,i,m);
if(!IsStrEqual(&sub,t)) i++;
else return i;
}
}
return 0;
}
思路二:KMP算法(1977)
每当一趟匹配过程中出现字符比较不相等时,不回溯主串指针,而是将模式串向右滑动恰当位置,继续比较——挖掘了模式串内在的关联信息
对于模式串 P = p 0 p 1 p 2 … p j − 1 p j . . . p n P=p_0 p_1 p_2 …p_{j-1}p_j...p_n P=p0p1p2…pj−1pj...pn
记录某一个k值,使得
p 0 p 1 … p k + 1 ≠ p j − k − 2 p j − k − 1 … p j − 1 p_0p_1 …p_{k+1}≠p_{j-k-2}p_{j-k-1}…p_{j-1} p0p1…pk+1=pj−k−2pj−k−1…pj−1
且 p 0 p 1 … p k = p j − k − 1 p j − k … p j − 1 p_0 p_1 …p_k = p_{j-k-1}p_{j-k}…p_{j-1} p0p1…pk=pj−k−1pj−k…pj−1
那么当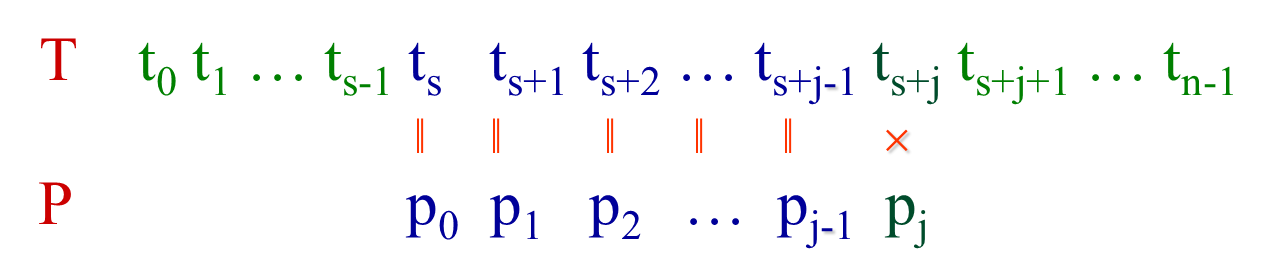
下一趟可以直接用 t s + j t_{s+j} ts+j与 p k + 1 p_{k+1} pk+1与 继续比较,因为前面都相等
PS:一些说明


消除了每趟失配后为实施下一趟比较时对主串指针的回退,避免了对已被匹配过的字符的再检查
提高了模式匹配效率,令主串的长度是n,模式串的长度是m,则算法的时间复杂度: O ( m + n ) O(m+n) O(m+n)
引入next数组/next特征向量用于记录当前字符前能以前缀子串匹配的最长长度k,那么k可以直接定位到下一次匹配的字符的位置
PS:注意图中的括号的左闭右开和左开右闭
设模式串 P = p 0 p 1 … p m − 2 p m − 1 P = p_0p_1… p_{m-2}p_{m-1} P=p0p1…pm−2pm−1
令 S e t X = 0 < k < j ∣ P [ 0.. k ) = P [ j − k . . j ) SetX={0<k<j | P[0..k) = P[j-k .. j)} SetX=0<k<j∣P[0..k)=P[j−k..j)
n e x t [ j ] = m a x ( S e t X ) next[j] = max (SetX) next[j]=max(SetX)
- 若 S e t X SetX SetX为空,那么 n e x t [ j ] = 0 next[j]=0 next[j]=0
- 当 j = 0 j=0 j=0,P的j位置前的串为空串,空串没有真子串,所以SetX为空集。令 n e x t [ 0 ] = − 1 next[0] = -1 next[0]=−1
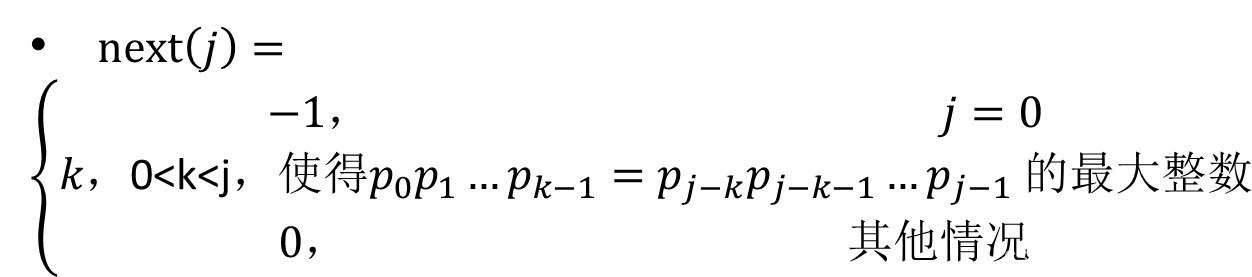
Q:如何求next[j]?
令 n e x t [ j ] = k next[j] = k next[j]=k,表示在模式串P 的 P [ 0 , j ) P[0,j) P[0,j) 中,自匹配的真前缀和真后缀的最大长度为k,那么, n e x t [ j + 1 ] = ? next[j+1]=? next[j+1]=?分两种情况: - 情况1:当 P [ j ] = P [ k ] P[j] = P[k] P[j]=P[k]时, n e x t [ j + 1 ] = n e x t [ j ] + 1 = k + 1 next[j+1] = next[j]+1 = k+1 next[j+1]=next[j]+1=k+1
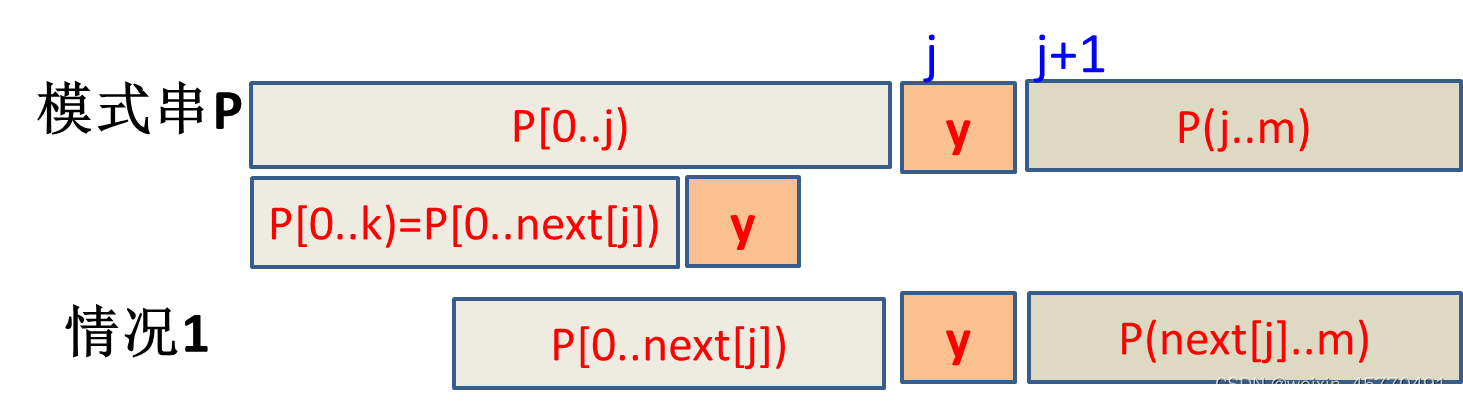
- 情况2:当 P [ j ] ≠ P [ k ] P[j] ≠ P[k] P[j]=P[k]时, n e x t [ j + 1 ] next[j+1] next[j+1]等于在 P [ 0.. n e x t [ j ] ) P[0..next[j]) P[0..next[j])的真前缀与 P [ 0.. j + 1 ) P[0..j+1) P[0..j+1)中真后缀匹配的最大长度
因为 n e x t [ j ] = k next[j] = k next[j]=k,所以 P [ j − k , . . j ) = P [ 0.. n e x t [ j ] ) P[j-k,..j)=P[0..next[j]) P[j−k,..j)=P[0..next[j]),求 P [ 0.. n e x t [ j ] ) P[0..next[j]) P[0..next[j])的真前缀与 P [ 0.. j + 1 ) P[0..j+1) P[0..j+1)中真后缀匹配的最大长度等价于求 P [ 0.. n e x t [ j ] ) P[0..next[j]) P[0..next[j])的真前缀与 P [ 0.. n e x t [ j ] ) P[0..next[j]) P[0..next[j])中真后缀匹配的最大长度→next[next[j]]=next[k]
代码实现:
void GetNext (HString *pattern, int next[]){
int j, k;
j=0; //j: 模式子串的位置
k= -1; //k: 模式自匹配指针
next[0]= -1;
while(j<pattern->length)
if(k== -1 || pattern->ch[j] == pattern->ch[k]) {
j++; k++;
next[j]=k;
} //失配
else k=next[k];
}
// 若模式串长度为m,则时间复杂度为O(m)
还可以对Next数组进行优化→ nextval:
将主串的S[i]、模式串的P[k]进行匹配。若P[k]=P[j],那么匹配一定不成功,串还要右滑,滑到next[k]位置。所以,可以直接将j的next值改成 next[k]。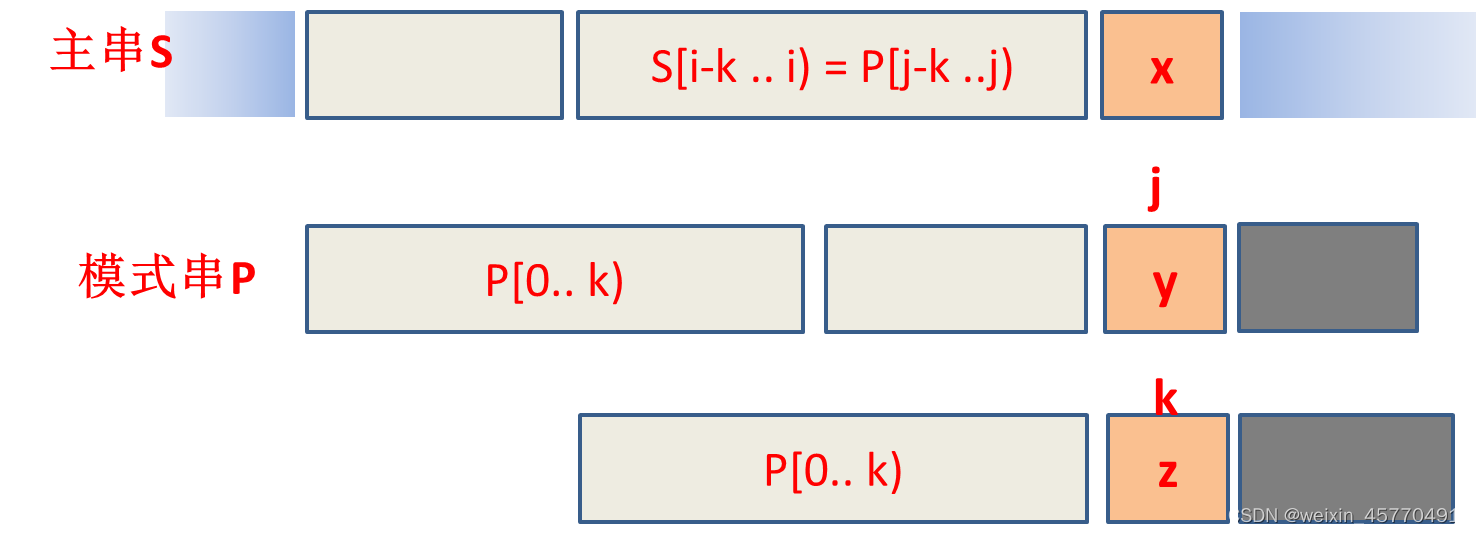
void GetNextVal(HString *pattern,int nextval[]){
int j,k; j=0;k= -1; nextval[0]= -1;
while(j<pattern->length)
if(k== -1 || pattern->ch[j] == pattern->ch[k]){
j++;k++;
if(pattern->ch[j] == pattern->ch[k]) nextval[j]=nextval[k];
else nextval[j]=k;
}
else k=nextval[k];
}
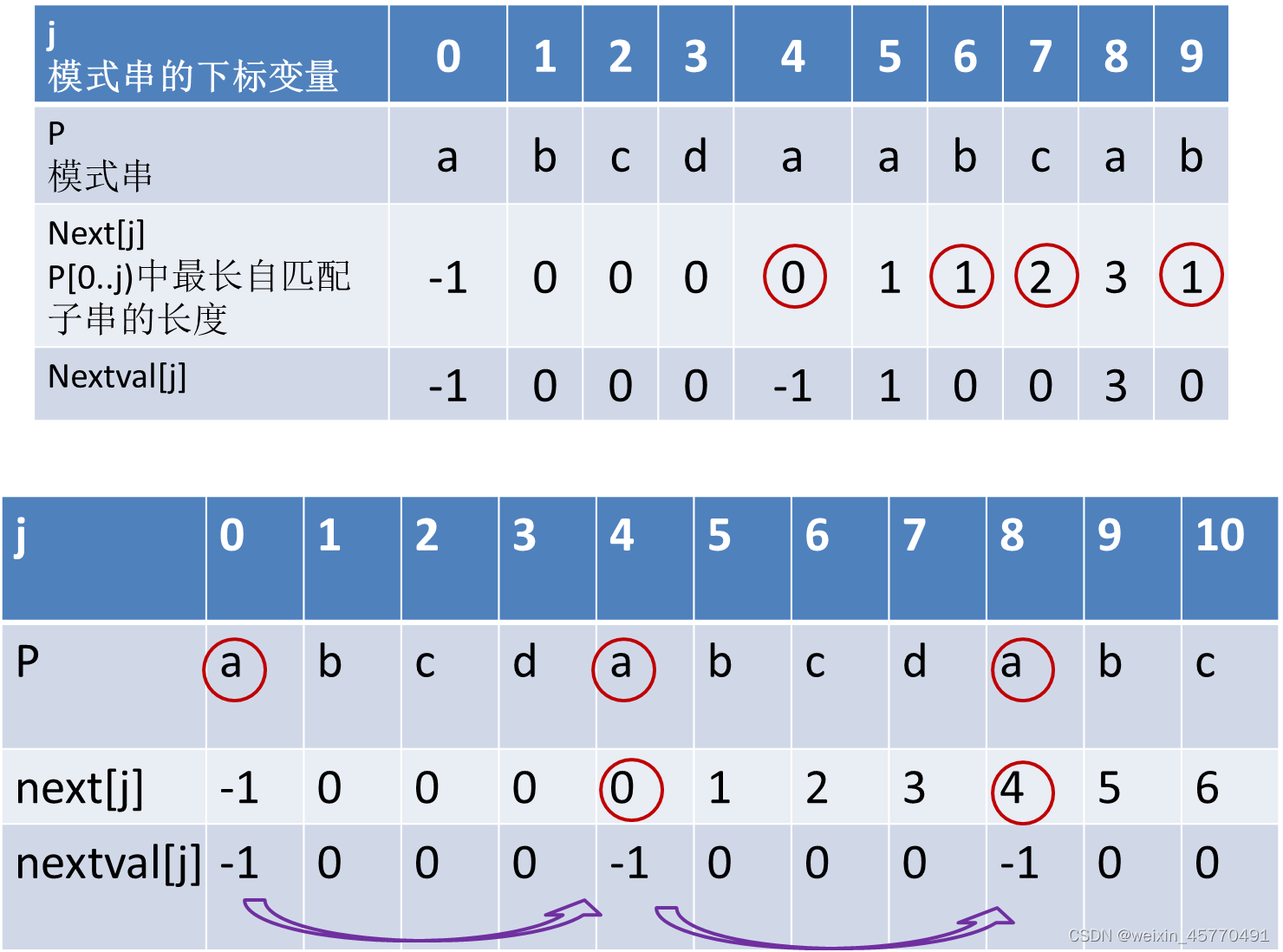
求字符串匹配举例: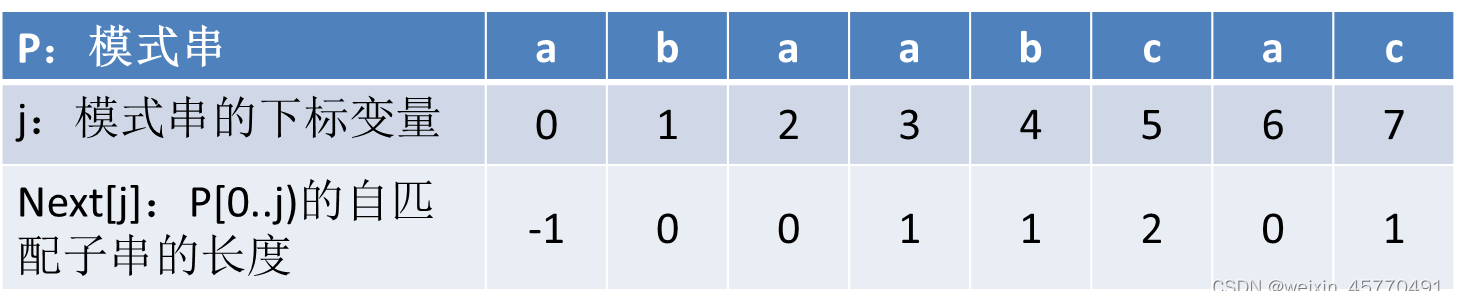
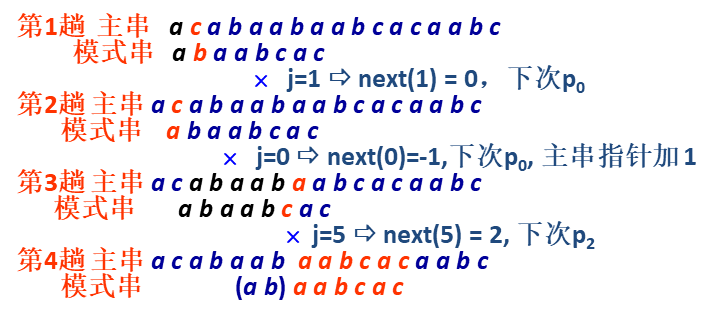
那么字符串匹配的实现为:
int StrIndexKMP(HString *s, HString *t, int pos) {
int next[INITSTRLEN]; GetNext(t, next);
int i,j;
i=pos-1; j=0;
while(i<s->length && j<t->length)
if(j== -1 || s->ch[i] == t->ch[j]) {i++;j++;}
else j=next[j];
if(j>=t->length)
return i -t->length+1;
//返回s中与t匹配的子序列第一个字符的序号
else
return 0; //走到主串末尾,匹配失败
}
总结:
KMP算法的优点:主串指针不回溯,算法的时间复杂度低,特别适用于模式串与主串之间存在许多部分匹配的情况
串操作应用举例
从文件读入书名、书号,建立关键字索引表
- 词表:线性表,顺序表示,线性表的元素是串
- 索引表:线性表,为方便查找,采用顺序存储结构,并保持字典序
关键字:串,堆分配存储表示,节省空间
书号:与关键字对应的书号个数不等,线性表,单链表

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容






所有评论(0)