数据结构与算法(C++)-算法
数据结构与算法(C++)——算法
参考:
1.0 十大经典排序算法 | 菜鸟教程 (runoob.com)
六大排序算法:插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序-CSDN博客
1、排序
1.1、冒泡排序
重复遍历待排序的序列,每次比较相邻的两个元素并判断是否交换,直到没有需要交换为止。
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
void bubble_sort(vector<int>& vec) {
int n = vec.size();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - 1 - i; j++) {
if (vec[j] > vec[j + 1]) { // ascending
swap(vec[j + 1], vec[j]);
}
}
}
}1.2、选择排序
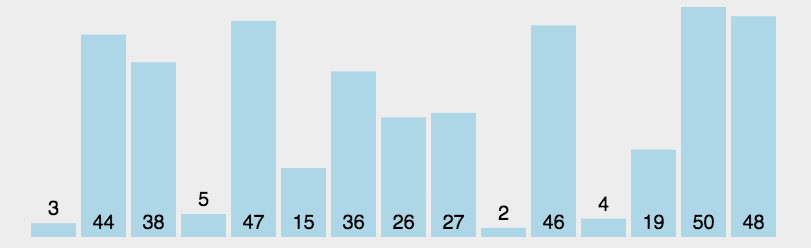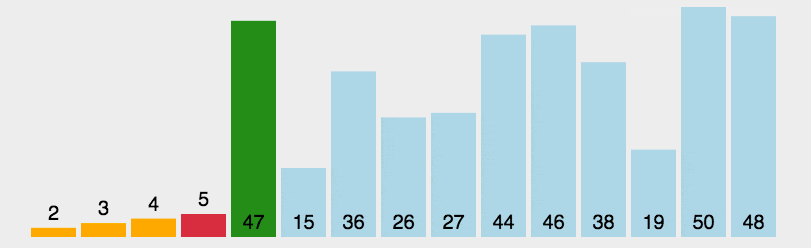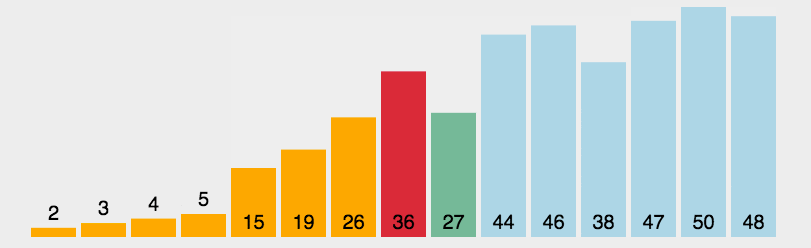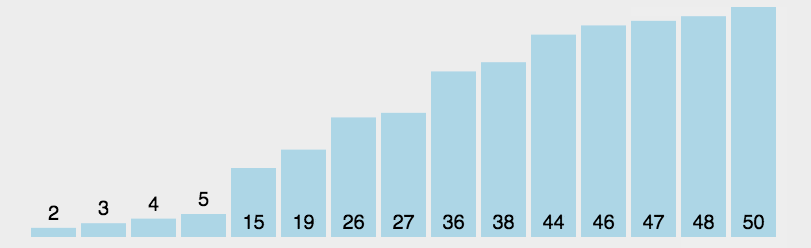
每次从未排序序列中选出最小(或最大)的元素,放到已排序序列的末尾。
是否可以同时选择最大的、最小的?
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
void selection_sort(vector<int>& vec) {
int n = vec.size();
for (int i = 0; i < n; i++) {
int minimum = vec[i]; // ascending
int pos = i; // record the minimum and its position
for (int j = i; j < n; j++) {
if (minimum > vec[j]) { // look for the minimun in the rest
minimum = vec[j];
pos = j;
}
}
vec[pos] = vec[i];
vec[i] = minimum; // inesrt the selected minimum element
}
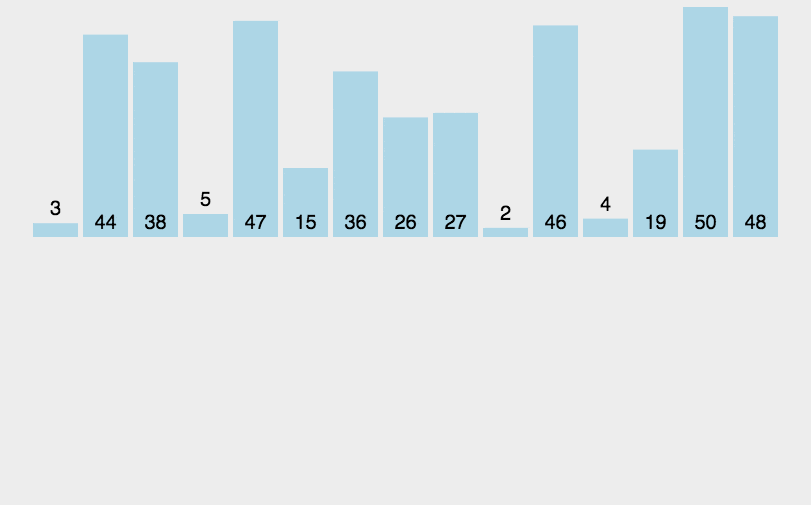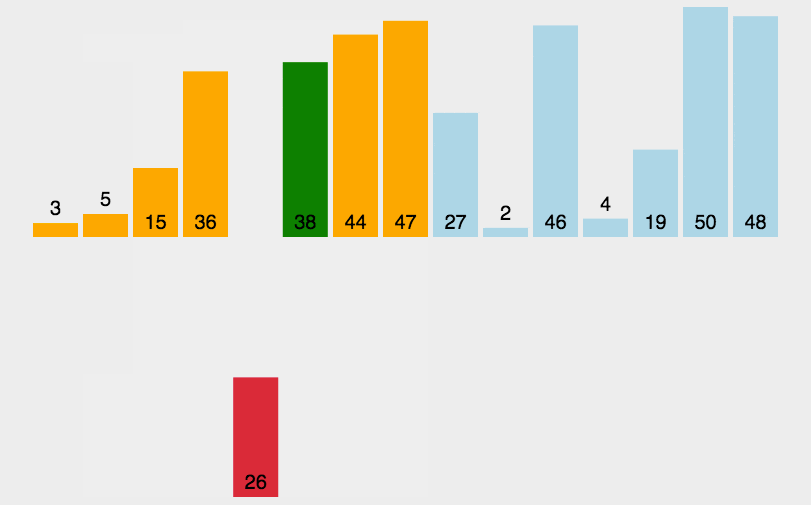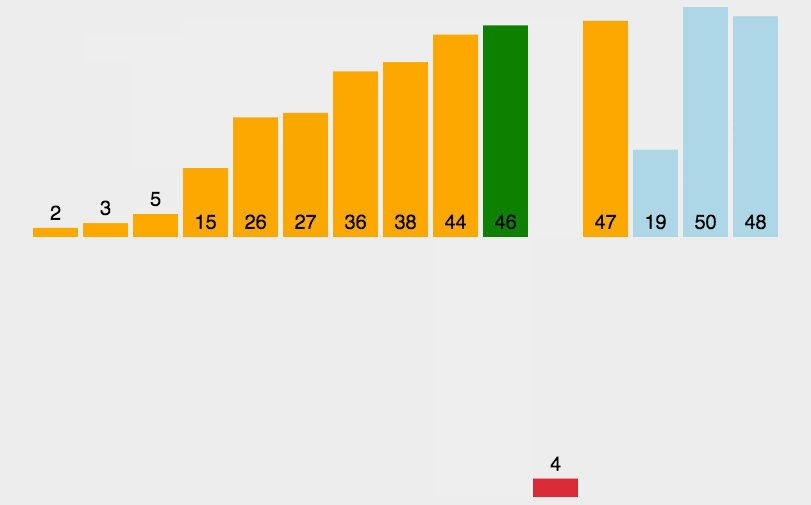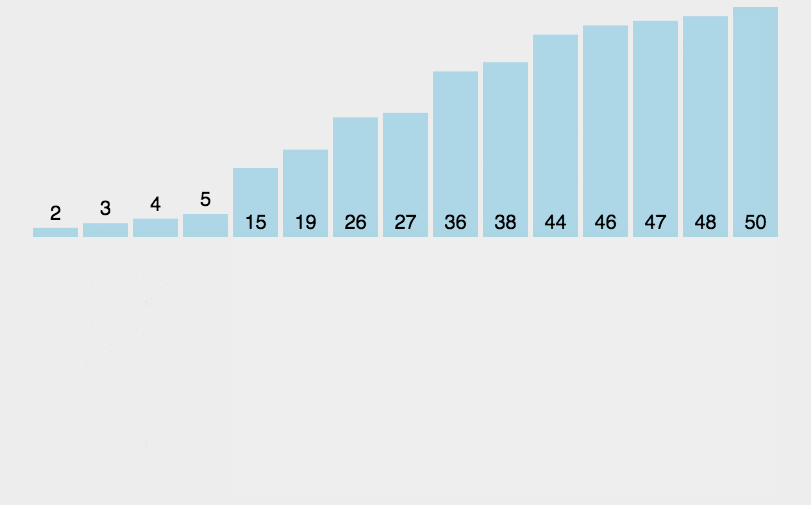
}1.3、插入排序
将未排序的元素插入到已排序序列中的适当位置。默认第一个元素已排好。
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
void insertion_sort(vector<int>& vec) {
int n = vec.size();
for (int i = 1; i < n; i++) { // consider that the first one is ordered
for (int j = i; j > 0; j--) { // swap the two elements from behind
if (vec[j - 1] > vec[j]) { // ascengding
swap(vec[j - 1], vec[j]);
}
else { // the proper position
break;
}
}
}
}1.4、希尔排序
改进的插入排序,也称为递减增量排序算法,通过比较相距一定间隔的元素来进行排序,以此来减少数据交换的次数,提高排序效率。希尔排序的核心思想是将待排序列分割成若干子序列分别进行插入排序,每次子序列的长度递减,直至1,例如n/2, n/4, ..., 1。子序列间的比较是在子序列中相同位置的元素进行比较,即相隔子序列长度整数倍的两个元素进行比较。当子序列长度为1时,和普通插入排序一样。

- 时间复杂度:
- 最坏情况下:O(n^2)(与增量序列选择有关,某些增量序列可以达到O(n log n))
- 平均情况下:O(n^1.5)
- 空间复杂度:O(1)
void shell_sort(vector<int>& vec) {
int n = vec.size();
for (int gap = n / 2; gap > 0; gap /= 2) { // descending gap
for (int i = gap; i < n; ++i) { // insertion_sort for every subseq
// compare the elem in the current subseq with the elem with the same order in the previous subseq
for (int j = i; j >= gap && vec[j - gap] > vec[j]; j -= gap) { // ascending
swap(vec[j], vec[j - gap]);
}
}
}
}1.5、归并排序
基于分治法的有效、稳定的排序算法。将数组分成两部分,分别排序后再合并成一个有序序列。可用递归或迭代来进行分、治。
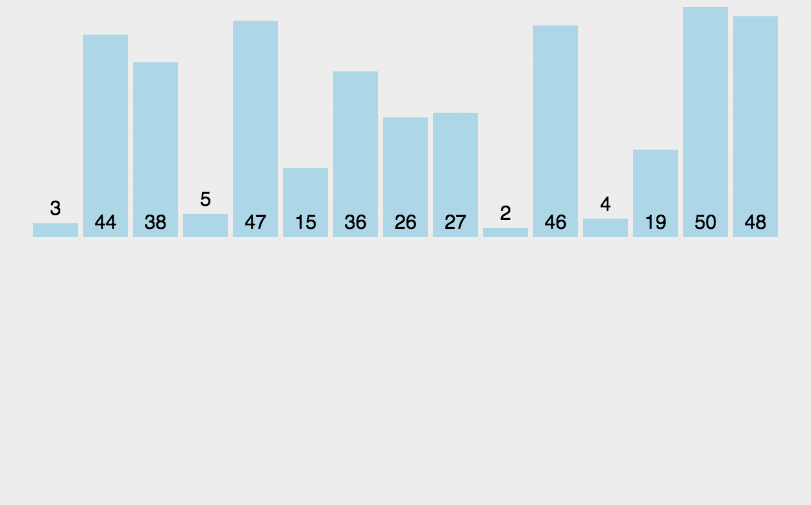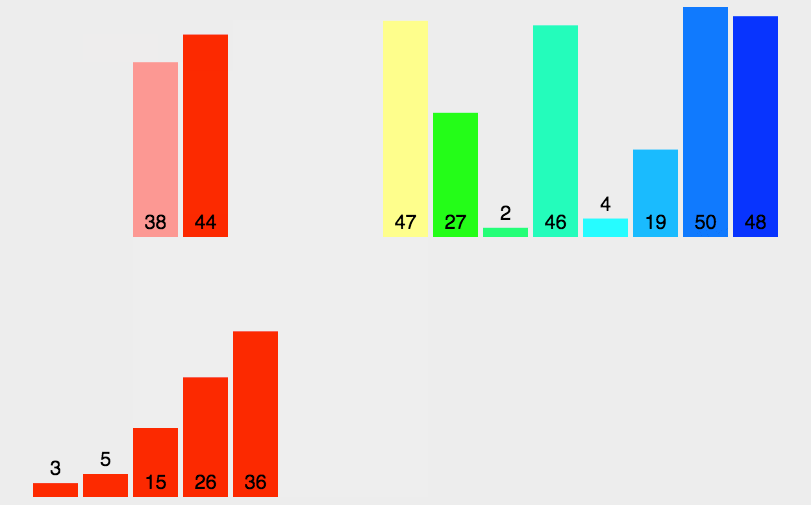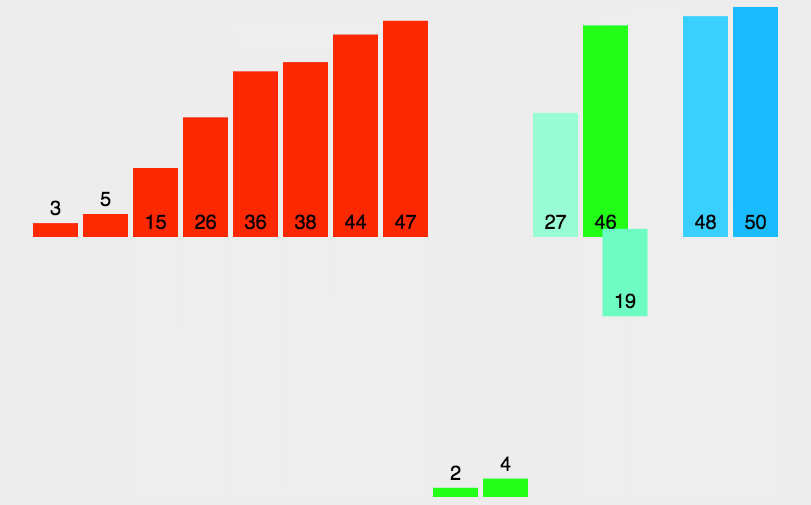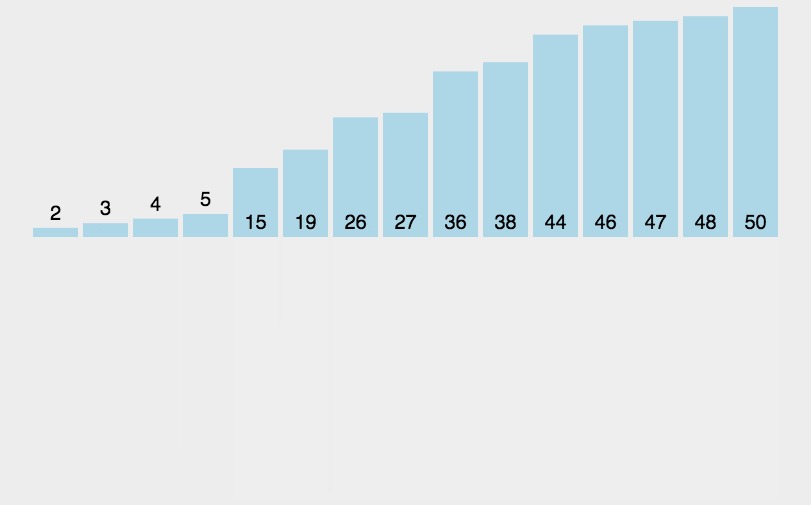
- 时间复杂度:O(n log n)
- 空间复杂度:O(n)
递归法:(递归深度大可能会栈溢出)
void merge_sort_recursion(vector<int>& vec, int start, int end) {
if (start >= end) return;
int mid = (start + end) / 2;
merge_sort_recursion(vec, start, mid); // divide
merge_sort_recursion(vec, mid + 1, end);
merge(vec, start, mid, end); // conquer
}
void merge(vector<int>& vec, int start, int mid, int end) {
// put the elems to be compared into two new arrays
vector<int> left(vec.begin() + start, vec.begin() + mid + 1);
vector<int> right(vec.begin() + mid + 1, vec.begin() + end + 1);
// put the elems had compared into original array
int left_index = 0;
int right_index = 0;
left.emplace_back(numeric_limits<int>::max()); // avoid array being out of range
right.emplace_back(numeric_limits<int>::max()); // due to the remaining elems in arrays
for (int i = start; i <= end; i++) {
if (left[left_index] <= right[right_index]) { // ascending
vec[i] = left[left_index];
left_index++;
}
else {
vec[i] = right[right_index];
right_index++;
}
}
}迭代法:
void merge_sort_iteration(vector<int>& vec) {
int n = vec.size();
for (int scale = 1; scale < n; scale += scale) { // the scale of subsequence
for (int start = 0; start < n - 1; start += 2 * scale) { // the start index of subseq at different scale
// put the elems to be compared into two new arrays
int mid = start + scale - 1;
int end = min(start + 2 * scale - 1, n - 1);
vector<int> left(vec.begin() + start, vec.begin() + mid + 1);
vector<int> right(vec.begin() + mid + 1, vec.begin() + end + 1);
// put the elems had compared into original array
int left_index = 0;
int right_index = 0;
left.emplace_back(numeric_limits<int>::max()); // avoid array being out of range
right.emplace_back(numeric_limits<int>::max());
for (int i = start; i <= end; i++) {
if (left[left_index] <= right[right_index]) { // ascending
vec[i] = left[left_index];
left_index++;
}
else {
vec[i] = right[right_index];
right_index++;
}
}
}
}
}1.6、快速排序
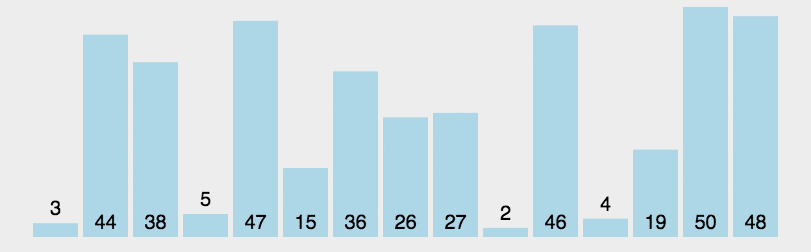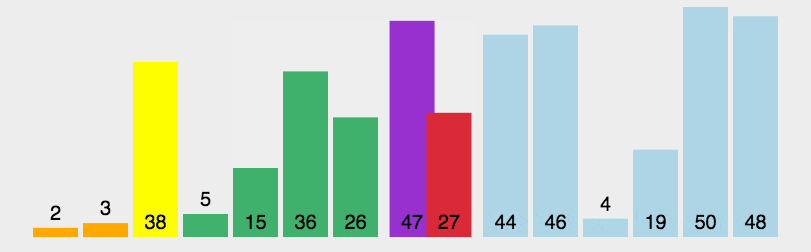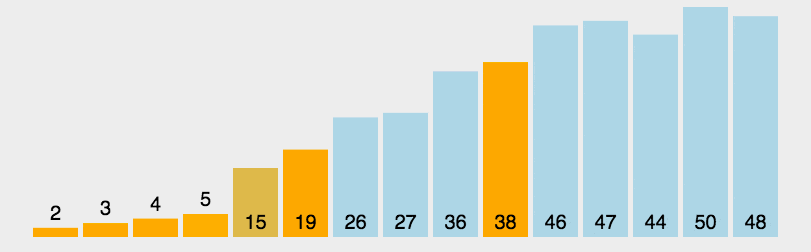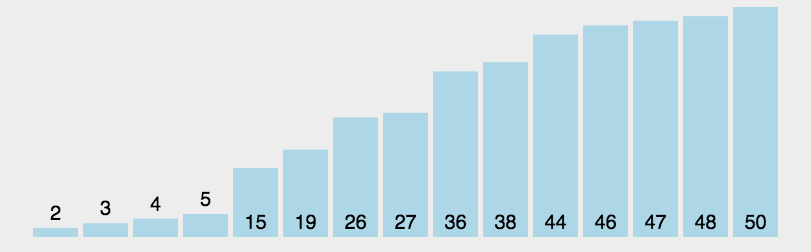
通过选择一个“基准”元素,将数组分成比基准小和比基准大的两部分,再递归地对两部分进行排序。
- 时间复杂度:平均O(n log n),最坏O(n^2)
- 空间复杂度:O(log n)
左右指针法(foare):递归。左指针指向大于pivot的元素,右指针指向小于pivot的元素,执行交换。当左右指针相遇时,与pivot交换,并返回pivot的实际位置。参数表中left、right初始只能指向数组的首尾。hoare_partition过程如下gif:

int hoare_partition(vector<int>& vec, int left, int right) {
int pivot = vec[left]; // select the leftmost elem as the pivot
int left_ptr = left; // pointer starts from the left
int right_ptr = right; // pointer starts from the right
while (left_ptr < right_ptr) { // ascending
while (vec[right_ptr] >= pivot && left_ptr < right_ptr) { // look for the elem less than the pivot in the right part
right_ptr--;
}
while (vec[left_ptr] <= pivot && left_ptr < right_ptr) { // look for the elem greater than the pivot in the left part
left_ptr++;
}
swap(vec[left_ptr], vec[right_ptr]);
}
swap(vec[left], vec[right_ptr]); // put the pivot to the proper position
return right_ptr; // return the position of the pivot
}
void quick_sort(vector<int>& vec, int left, int right) {
if (left >= right) return;
int pivot = hoare_partition(vec, left, right); // partition the array bu the pivot
quick_sort(vec, left, pivot);
quick_sort(vec, pivot + 1, right);
}前后指针法:递归。前指针指向大于pivot的元素的前一位,后指针指向小于pivot的元素,将前指针后移一位,执行交换。循环结束时,前指针将指向序列中最后一个大于pivot元素的前一位,将前指针后移一位,与pivot进行交换,并返回交换后pivot的实际位置。参数表中start、end初始只能指向数组的首尾。
int partition(vector<int>& vec, int start, int end) {
int pivot = vec[end]; // select the right-most elem as the pivot
int pre = start - 1; // pre pointer originally points to the previous position of the start of array
for (int cur = pre + 1; cur < end; cur++) {
if (vec[cur] <= pivot && pre++ != cur) { // ascending
// cur pointer points to the elem less than pivot
// pre pointer points to the elem greater than pivot
swap(vec[pre], vec[cur]);
}
}
swap(vec[pre + 1], vec[end]); // pre pointer points to the last elem greater than pivot, swap
return pre + 1; // return the pos of pivot
}
void quick_sort(vector<int>& vec, int start, int end) {
if (start >= end) return;
int pivot = partition(vec, start, end); // partition the array by the pivot
quick_sort(vec, start, pivot - 1); // sort the elems on both sides of the pivot
quick_sort(vec, pivot + 1, end);
}1.7、堆排序
利用堆这种数据结构,将数组看作一个完全二叉树,通过不断调整堆来进行排序。首先构造一个大顶堆(根节点最大),将堆顶与堆底元素互换,重复构造大顶堆,将堆顶元素与堆中倒数第二个元素互换,直至有序。升序通过构造大顶堆,降序通过构造小顶堆。
- 时间复杂度:O(n log n)
- 空间复杂度:O(1)
迭代法构建完全二叉树:
void max_heapify(vector<int>& vec, int start, int end) {
int father = start; // father node
int child = father * 2 + 1; // left child node, indexed by level traversal
while (child <= end) {
if (child + 1 <= end && vec[child] < vec[child + 1]) // choose the greater child node
child++;
if (vec[father] > vec[child]) // compare the father node and the greater child node
return;
else { // if the father node is less than child node
swap(vec[father], vec[child]); // swap the father node and child node
father = child; // compare the child node and grandchild node
child = father * 2 + 1;
}
}
}
void heap_sort(vector<int>& vec) {
int n = vec.size();
for (int i = n / 2 - 1; i >= 0; i--) { // initilization
max_heapify(vec, i, n - 1); // build the max heap
}
for (int i = n - 1; i > 0; i--) {
swap(vec[0], vec[i]); // swap the top and buttom of the heap
max_heapify(vec, 0, i - 1); // max_heapify the rest elems
}
}1.8、桶排序
将元素分到不同的桶中,每个桶内分别排序,然后将所有桶中的元素合并。
- 时间复杂度:O(n + k)
- 空间复杂度:O(n + k)
隐式指定桶的数量、大小,并处理异常大的元素。
template<typename T>
void bucket_sort(vector<T>& vec) {
int bucket_num = vec.size(); // the number of buckets equals to the size of array
if (bucket_num <= 0 ) return;
T maximum = vec[0];
T minimum = vec[0];
for (T elem : vec) { // look for the maximum and the minimum in the array
if (elem > maximum) maximum = elem;
if (elem < minimum) minimum = elem;
}
if (maximum == minimum) return;
float bucket_size = (maximum - minimum) / (bucket_num * 1.0); // the size of buckets > 0.0
vector<vector<T>> buckets(bucket_num); // build the buckets
for (int i = 0; i < bucket_num; ++i) { // allocate the elems into the proper bucket
int bucket_index = static_cast<int>((vec[i] - minimum) / bucket_size);
if (bucket_index <= bucket_num - 1) {
buckets[bucket_index].emplace_back(vec[i]);
}
else { // handle the expect elem which is too great
buckets[bucket_num - 1].emplace_back(vec[i]);
}
}
int index = 0;
for (auto bucket : buckets) {
if (bucket.empty()) continue;
sort(bucket.begin(), bucket.end()); // sort the elems in each bucket
for (T elem : bucket) { // merge the elems in all buckets
vec[index++] = elem;
}
}
}1.9、计数排序
通过计数每个元素出现的次数来排序,适用于元素范围有限的情况。
- 时间复杂度:O(n + k) (k 是数值范围)
- 空间复杂度:O(n + k)
1.10、基数排序
按照各个位数上的值进行多次排序,从最低位到最高位。
- 时间复杂度:O(d(n + k)) (d 是位数)
- 空间复杂度:O(n + k)
2、动态规划
动态规划(Dynamic Programming,DP)是一种算法设计方法,用于解决具有重叠子问题和最优子结构性质的问题。它通过将问题分解为子问题,记录子问题的解来避免重复计算,从而提高效率。动态规划广泛应用于最优化问题,如最短路径、最长子序列、背包问题等。设计困难,时间复杂度高
基本思想:
重叠子问题:问题可以分解为相同的子问题,并且这些子问题会被多次重复计算。
最优子结构:问题的最优解包含其子问题的最优解。
状态转移方程:通过递推关系,从子问题的解构造出原问题的解。
步骤:
定义状态:明确问题的子问题及其状态表示。
状态转移方程:找到状态之间的关系,构造递推公式。
初始条件和边界条件:确定基础子问题的解。
计算顺序:根据状态转移方程和初始条件,按照一定顺序计算子问题的解。
返回结果:根据计算得到的子问题解,得出原问题的解。
最长子序列:
int longestCommonSubsequence(const std::string& X, const std::string& Y) {
int m = X.size();
int k = Y.size();
// 避免处理边界条件,在前面多加一行一列,从[1,1]开始
std::vector<std::vector<int>> dp(m + 1, std::vector<int>(k + 1, 0));
// 初始条件dp[1][0]=0 dp[0][1]=0
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= k; ++j) {
if (X[i - 1] == Y[j - 1]) { // 状态转移方程
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else {
dp[i][j] = std::max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][k];
}
背包问题(物品不可分割):n个不同价值、重量的物品,选出总重量小于w的最大价值总和。
int knapsack(int W, const std::vector<int>& weights, const std::vector<int>& values) {
int n = weights.size();
std::vector<std::vector<int>> dp(n + 1, std::vector<int>(W + 1, 0)); // 对每个重量求最大值
// i为前i个物品,w为背包总重量,dp[i][w]为该条件下的最大价值
for (int i = 1; i <= n; ++i) {
for (int w = 0; w <= W; ++w) { // 递归(状态转义方程
if (weights[i - 1] <= w) { // 若第i个物品的重量小于背包限制重量w,就可以放进去
// 在背包重量限制为w下的最大价值就是 max(前i-1个物品最大价值, 把第i个物品放进去后的最大价值)
// 把第i个物品放进去后的最大价值 = 前i-1个物品在(w-第i个物品重量)下的最大价值 + 第i个物品的价值
dp[i][w] = std::max(dp[i - 1][w], dp[i - 1][w - weights[i - 1]] + values[i - 1]);
}
else { // 若第i个物品放不进去,那么在背包重量限制为w下,前i个物品最大价值 = 前i-1个物品最大价值
dp[i][w] = dp[i - 1][w];
}
std::cout << i << " " << w << " " << dp[i][w]<< std::endl;
}
}
return dp[n][W];// i=5,W=50时,是最终解
}
目标和(leetcode 494):n个非负整数,通过加减使之和为target,有多少种组合方案。
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for(int num : nums){ // 这些数的总和
sum += num;
}
if(sum < target || (sum - target) % 2 == 1 ) return 0; // 由于是整数,sum-target必须是2的倍数
int len = nums.size();
// 问题转化,n个数加减的和为target,即选出哪些数为负,设所有选为负的数和为x,那保持为正的数总和为sum-x,得方程(sum-x)-x=target。
// 因此只要选出总和为(sum-target)/2的数,将其减去,即符合题意。
int real_target = (sum - target) / 2;
vector<vector<int>> dp(len + 1, vector<int>(real_target + 1)); // dp[i][j]为前i个数和为j的方案个数
for(int j = 0; j <= real_target; j++) dp[0][j] = 0; // 初始条件
dp[0][0] = 1;
for(int i = 1; i <= len; i++){ // 状态转移方程
for(int j = 0; j <= real_target; j++){
dp[i][j] = dp[i - 1][j]; // 不选第i个数的方案个数(前i-1个数已经满足和为j,后面的数都可以不选)
if(j >= nums[i - 1]){
dp[i][j] += dp[i - 1][j - nums[i - 1]]; // 选第i个数的方案个数(若第i个数小于等于j,方案个数等于前i-1个数的和等于j减去第i个数的方案个数)
}
}
}
return dp[len][real_target];
}3、贪心算法
贪心算法(Greedy Algorithm)是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望能够得到全局最优解的一种算法设计策略。贪心算法在许多问题中都能得到最优解,但并不是所有问题都适用。应用场景有:最小生成树(如Kruskal和Prim算法)、最短路径问题(Dijkstra算法)、活动选择问题(选择最多的非重叠活动)、背包问题、哈夫曼编码。简单易实现,但不能保证所有问题的最优解。
基本思想:
贪心选择性质:可以通过局部最优选择来达到全局最优解。
最优子结构性质:问题的最优解包含其子问题的最优解。(与动态规划类似)
步骤:
选择贪心策略:确定在每一步选择中应该采取的局部最优选择。
证明贪心选择的正确性:证明通过贪心选择可以得到全局最优解。
构造最优解:通过一次次贪心选择构造出问题的最优解。
活动选择问题:
struct Activity { // 记录活动的开始时间、结束时间
int start, end;
};
bool compare(Activity a1, Activity a2) { // 仿函数,用于按结束时间升序排序
return a1.end < a2.end;
}
vector<Activity> activitySelection(vector<Activity>& activities) {
sort(activities.begin(), activities.end(), compare); // 将活动时间按结束时间升序排序
vector<Activity> selectedActivities;
int lastEnd = -1; // 初始化第一个结束时间
for (const auto& activity : activities) {
// 贪心策略:选择结束时间最早,并且与已选择活动不冲突的活动
if (activity.start >= lastEnd) { // 开始时间晚于上一个活动的结束时间,不冲突
selectedActivities.push_back(activity);
lastEnd = activity.end;
}
}
return selectedActivities;
}
背包问题(物品可分割):
struct Item { // 记录每个物体的重量、价值
int weight;
int value;
};
bool compare(Item a, Item b) { // 仿函数,按物体的单位重量价值降序排序
double r1 = (double)a.value / a.weight;
double r2 = (double)b.value / b.weight;
return r1 > r2;
}
double fractionalKnapsack(int W, vector<Item>& items) {
sort(items.begin(), items.end(), compare); // 按(价值/重量)降序排序
int currentWeight = 0;
double finalValue = 0.0;
// 贪心策略:每次选择单位价值最大的物品
for (const auto& item : items) {
if (currentWeight + item.weight <= W) {
currentWeight += item.weight;
finalValue += item.value;
}
else { // 剩余重量不够时,将物品分割
int remain = W - currentWeight;
finalValue += item.value * ((double)remain / item.weight);
break;
}
}
return finalValue;
}
int main() {
int W = 50; // 背包容量
vector<Item> items = { {10, 60}, {20, 100}, {30, 120} };
cout << "Maximum value in Knapsack = " << fractionalKnapsack(W, items) << endl;
return 0;
}
1111

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)