数据结构|C语言|图的基本操作、遍历(DFS、BFS)
图的基本操作 队列 链表 线性表 数据结构 深度优先遍历 广度优先遍历 DFS BFS C语言
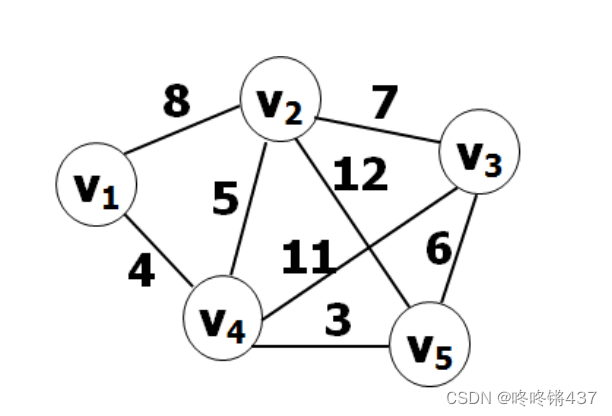
实现以下图的各种基本操作的程序:
① 用邻接矩阵作为储结构存储图G并输出该邻接矩阵;
② 用邻接链表作为储结构存储图G并输出该邻接链表;
③ 按DFS算法输出图G中顶点的遍历序列;
④ 按BFS算法输出图G中顶点的遍历序列;
⑤ 主函数通过函数调用实现以上各项操作。
①图的深度优先遍历DFS是从初始结点开始扩展,扩展顺序总是先扩展最新产生的结点。这就使得搜索沿着状态空间某条单一的路径进行下去,直到最后的结点不能产生新结点或者找到目标结点为止。当搜索到不能产生新的结点的时候,就沿着结点产生顺序的反方向寻找可以产生新结点的结点,并扩展它,形成另一条搜索路径。
由于在深度优先搜索算法中,要满足先生成的结点后扩展的原则,所以存储结点的表一般采用栈这种数据结构。
深度优先搜索算法的搜索步骤一般是:
I.从初始结点开始,将待扩展结点依次放到栈中。
II.如果栈空,即所有待扩展结点已全部扩展完毕,则问题无解,退出。
III.取栈中最新加入的结点,即栈顶结点出栈,并用相应的扩展原则扩展出所有的子结点,并按顺序将这些结点放入栈中。若没有子结点产生,则转II。
V.如果某个子结点为目标结点,则找到问题的解(这不一定是最优解),结束。如果要求得问题的最优解,或者所有解,则转II,继续搜索新的目标结点。
来源:DFS(一):深度优先搜索的基本思想 - aTeacher - 博客园 (cnblogs.com)
②图的广度优先遍历BFS从初始节点开始,应用算符生成第一层节点,检查目标节点是否在这些后继节点中,若没有,
再用产生式规则将所有第一层的节点逐一扩展,得到第二层节点,并逐一检查第二层节点中是否包含目标节点。
若没有,再用算符逐一扩展第二层的所有节点……,如此依次扩展,检查下去,直到发现目标节点为止。
为了便于进行搜索,要设置一个表存储所有的结点。由于在广度优先搜索算法中,要满足先生成的结点先扩展的原则,所以存储结点的表一般采用队列这种数据结构。
广度优先搜索算法的搜索步骤一般是:
I.从队列头取出一个结点,检查它按照扩展规则是否能够扩展,如果能则产生一个新结点。
II.检查新生成的结点,看它是否已在队列中存在,如果新结点已经在队列中出现过,就放弃这个结点,然后回到第I步。否则,如果新结点未曾在队列中出现过,则将它加入到队列尾。
III.检查新结点是否目标结点。如果新结点是目标结点,则搜索成功,程序结束;若新结点不是目标结点,则回到第I步,再从队列头取出结点进行扩展。
来源:BFS(一):广度优先搜索的基本思想 - aTeacher - 博客园 (cnblogs.com)
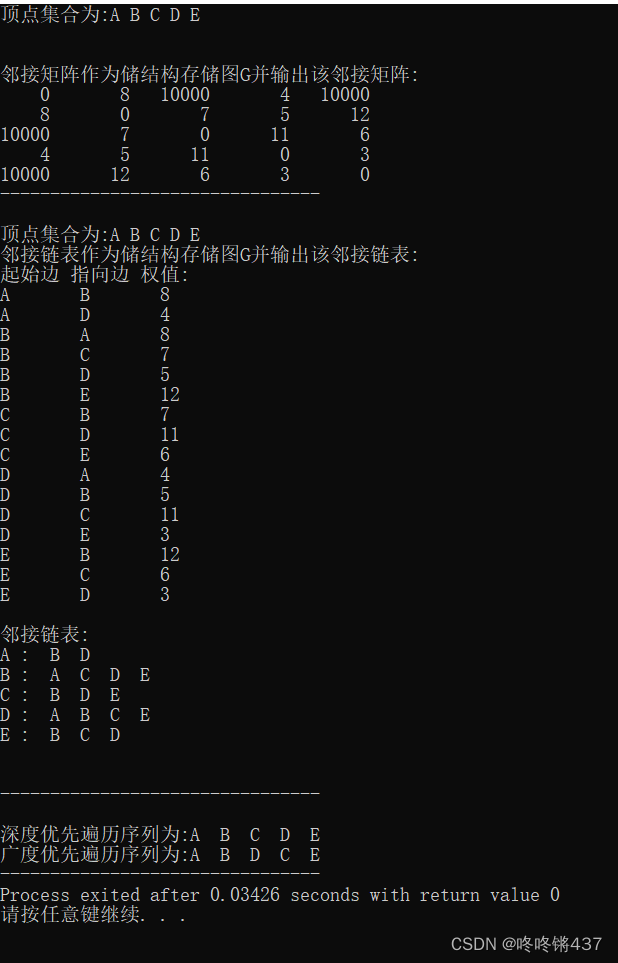
程序运行结构如下:
main.cpp
//main.cpp
#include<stdio.h>
#include<stdlib.h>
typedef char DataType;
#define MaxSize 100
#define MaxQueueSize 100
#define MaxVertices 10
#define MaxWeight 10000
#include "AdjMGraph.h"
#include "AdjMGraphCreate.h"
#include "AdjLGraph.h"
#include "AdjLGraphCreate.h"
int main()
{
AdjMGraph g1;
DataType a[] = {'A' , 'B' , 'C' , 'D' , 'E'};
RowColWeight rcw[] = {{0,1,8},{0,3,4},{1,0,8},{1,2,7},{1,3,5},
{1,4,12},{2,1,7},{2,3,11},{2,4,6},{3,0,4},
{3,1,5},{3,2,11},{3,4,3},{4,1,12},{4,2,6},{4,3,3}};
int n = 5 , e = 16;
int i , j;
CreateGraph(&g1,a,n,rcw , e);
printf("顶点集合为:");
for(i = 0 ; i < g1.Vertices.size ; i++)
printf("%c " , g1.Vertices.list[i]);
printf("\n");
printf("\n\n邻接矩阵作为储结构存储图G并输出该邻接矩阵:\n");
for(i = 0 ; i < g1.Vertices.size ; i++){
for(j = 0 ; j < g1.Vertices.size ; j++)
printf("%5d\t" , g1.edge[i][j]);
printf("\n");
}
printf("--------------------------------\n\n");
AdjLGraph g2;
CreateGraph(&g2 , a , n , rcw , e);
printf("顶点集合为:");
for(i = 0 ; i < g2.numOfVerts ; i++)
printf("%c " , g2.a[i].data);
printf("\n");
printf("邻接链表作为储结构存储图G并输出该邻接链表:\n");
printf("起始边 指向边 权值:\n");
for(i = 0 ; i < g2.numOfEdges ; i++){
printf("%c\t%c\t%d\n" , rcw[i].row+'0'+17 , rcw[i].col+'0'+17 , rcw[i].weight);
}
printf("\n邻接链表:\n");
Edge *p;
for(i = 0 ; i < g2.numOfVerts ; i++){
printf("%c : " , g2.a[i].data);
for(j = 0 ; j < e ; j++){
if(rcw[j].row == i)
printf("%c " , rcw[j].col+'0'+17);
}
printf("\n");
}
printf("\n\n--------------------------------\n\n");
printf("深度优先遍历序列为:");
DepthFirstSearch(g1,Visit);
printf("\n广度优先遍历序列为:");
BoradFirstSearch(g1,Visit);
return 0;
}
LinList.h
//单链表的基本操作 LinList.h
#include<stdio.h>
#include<stdlib.h>
typedef struct node{
DataType data;
struct node *next;
}SLNode;
//初始化ListInitiate(SLNode *head)
void ListInitiate(SLNode *head){
head = (SLNode *)malloc(sizeof(SLNode));
head->next = NULL;
}
//求当前数据元素个数 ListLength(SLNode *head)
int ListLength(SLNode *head){
SLNode *p = *head;
while(p->next != NULL){
size++;
p = p->next;
}
return size;
}
//插入数据 ListInsert(SLNode *head , int i , DataType x)
int ListInsert(SLNode *head , int i , DataType x){
SLNode *p = head;
int j;
SLNode *q = (SLNode *)malloc(sizeof(SLNode));
q->data = x;
for(j = 0 ; (j < i)&&(p->next != NULL) ; j++)
p = p->next;
if(j != i){
printf("插入元素位置参数错误!");
return 0;
}
q->next = p->next;
p->next = q;
return 1;
}
//删除ListDelete(SLNode *head , int i , DataType *x)
int ListDelete(SLNode *head , int i , DataType *x){
SLNode *p , *q;
int j;
p = head;
for(j = 0 ; (j < i-1) && (p->next != NULL); j++)
p = p->next;
if(j != i-1){
printf("输入元素位置参数错误!\n");
return 0;
}
*q = p->next;
*x = q->data;
p->next = q->next;
free(q);
return 1;
}
//取数据元素个数ListGet(SLNode *head , int i , DataType x)
int ListGet(SLNode *head , int i , DataType *x){
SLNode *p;
int j;
p = head;
j = -1;
while(p->next != NULL && j < i){
p = p->next;
j++;
}
if(j != i){
printf("取元素位置参数错误!\n");
return 0;
}
*x = p->data;
return 1;
}
//撤销单链表Destroy(SLNode *head)
void Destroy(SLNode *head){
SLNode *p , *p1;
p = head;
while(p != NULL){
p1 = p;
p = p->next;
free(p1);
}
head = NULL;
} SeqList.h
//顺序表的基本操作 SeqList.h
typedef struct{
DataType list[MaxSize];
int size;
}SeqList;
//初始化ListInitiate(L)
void ListInitiate(SeqList *L){
L->size = 0;
}
//求当前数据元素个数(L)
int ListLength(SeqList L){
return L.size;
}
//插入数据元素ListInsert(L , i , x)
int ListInsert(SeqList *L , int i , DataType x){
//插入成功返回1 失败返回0
int j;
if(L->size >= MaxSize){
printf("顺序表已满无法插入!\n");
return 0;
}
else if(i < 0 || i > L->size){
printf("参数i非法!\n");
return 0;
}
else{
for(j = L->size ; j > i ; j--)
L->list[j] = L->list[j-1];
L->list[i] = x;
L->size++;
return 1;
}
}
//删除数据元素ListDelete(L , i , x)
int ListDelete(SeqList *L , int i , DataType *x){
//成功返回1 失败返回0
int j;
if(L->size <= 0){
printf("顺序表已空无数据元素可删!\n");
return 0;
}
else if(i < 0 || i > L->size-1){
printf("参数i不合法!\n");
return 0;
}
else{
*x = L->list[i];
for(j = i + 1 ; j < L->size ; j++)
L->list[j-1] = L->list[j];
L->size--;
return 1;
}
}
//取数据元素ListGet(L , i , x)
int ListGet(SeqList L , int i , DataType *x){
if(i < 0 || i > L.size -1){
printf("参数i不合法!\n");
return 0;
}
*x = L.list[i];
return 1;
}
//Visit()
void Visit(DataType item){
printf("%c " , item);
} SeqCQueue.h
//SeqCQueue.h
typedef struct{ //顺序循环队列结构体
int rear; //尾指针
int front; //头指针
int count; //计数器
DataType queue[MaxQueueSize];
}SeqCQueue;
//初始化队列Q
void QueueInitiate(SeqCQueue *Q){
Q->rear = 0; //尾指针初始为0
Q->front = 0; //头指针初始为0
Q->count = 0; //计数器初始为0
}
//判断队列Q是否为空
int QueueNotEmpty(SeqCQueue Q){
//队列为空返回0 不空返回1
if(Q.count == 0) return 0;
else return 1;
}
//入队列操作
int QueueAppend(SeqCQueue *Q , DataType x){
//队尾插入数据x 插入成功返回1 失败返回0
if(Q->count > 0 && Q->rear == Q->front){
printf("队列已满无法插入 出错!\n");
return 0;
}
else{
Q->queue[Q->rear] = x;
Q->rear = (Q->rear + 1)%MaxQueueSize;
Q->count++;
return 1;
}
}
//出队列操作
int QueueDelete(SeqCQueue *Q , int *d){
//删除顺序循环队列队头元素并赋值给d 成功返回1 失败返回0
if(Q->count == 0){
printf("队列已空无法出队 出错!\n");
return 0;
}
else{
*d = Q->queue[Q->front]; //取出队头元素赋值给d
Q->front = (Q->front + 1)%MaxQueueSize; //更新队头指针 队头指针+1
Q->count--; //计数器-1
return 1;
}
}
//输出队列元素个数
void QueuePrintCount(SeqCQueue Q){
printf("Queue count: %d\n" , Q.count);
} AdjMGraph.h
//AdjMGraph.h
//邻接矩阵 邻接矩阵作为储结构存储图G
#include "SeqList.h" //包含顺序表头文件
#include "SeqCQueue.h" //包含顺序循环队列头文件
typedef struct{
SeqList Vertices; //存放顶点的顺序表
int edge[MaxVertices][MaxVertices]; //存放边的邻接矩阵
int numOfEdges; //边的条数
}AdjMGraph;
//初始化有n个顶点的顶点顺序表和邻接矩阵
void Initiate(AdjMGraph *G , int n){
int i , j;
for(i = 0 ; i < n ; i++){
for(j = 0 ; j < n ; j++){
if(i == j) G->edge[i][j] = 0;
else G->edge[i][j] = MaxWeight; //MaxWeight表示无穷大
}
}
G->numOfEdges = 0; //边的条数置为0
ListInitiate(&G->Vertices); //顺序表初始化
}
//在图G中插入顶点vertex
void InsertVertex(AdjMGraph *G , DataType vertex){
ListInsert(&G->Vertices , G->Vertices.size , vertex);
}
//在图G中插入边<v1,v2>,边<v1,v2>的权为weight
void InsertEdge(AdjMGraph *G , int v1 , int v2 , int weight){
if(v1 < 0 || v1 >= G->Vertices.size || v2 < 0 || v2 >= G->Vertices.size){
printf("参数v1或v2越界出错!\n");
return ;
}
G->edge[v1][v2] = weight;
G->numOfEdges++;
}
//删除边<v1,v2>
void DeleteEdge(AdjMGraph *G , int v1 , int v2){
if(v1 == v2 ||v1 < 0 || v1 >= G->Vertices.size || v2 < 0 || v2 >= G->Vertices.size){
printf("参数v1或v2出错!\n");
return ;
}
if(G->edge[v1][v2] == MaxWeight || v1==v2){
printf("该边不存在!\n");
return ;
}
G->edge[v1][v2] = MaxWeight;
G->numOfEdges--;
}
//在图G中寻找序号为v的顶点的第一个邻接顶点
int GetFirstVex(AdjMGraph G , int v){
int col;
if(v < 0 || v >= G.Vertices.size){
printf("参数v越界出错!\n");
return -1;
}
for(col = 0 ; col < G.Vertices.size ; col++){
if(G.edge[v][col] > 0 && G.edge[v][col] < MaxWeight)
return col;
}
return -1;
}
//取图G的下一个邻接顶点
int GetNextVex(AdjMGraph G , int v1 , int v2){
int col;
if(v1 < 0 || v1 >= G.Vertices.size || v2 < 0 || v2 >= G.Vertices.size){
printf("参数v1或v2越界出错!\n");
return -1;
}
for(col = v2+1 ; col < G.Vertices.size ; col++){
if(G.edge[v1][col] > 0 && G.edge[v1][col] < MaxWeight)
return col;
}
return -1;
}
//连通图的深度优先遍历函数
void DepthFSearch(AdjMGraph G , int v , int visited[] , void Visit(DataType item)){
//连通图G以v为起始顶点的、访问操作为Visit()的深度优先遍历
//数组visited标记相应顶点是否已经被访问过(0表示未访问过,1表示已访问过)
int w;
Visit(G.Vertices.list[v]); //访问顶点v
visited[v] = 1; //将顶点v置为已访问标记
w = GetFirstVex(G , v); //取第一个邻接顶点
while(w != -1){
if(!visited[w]) //如果w未被访问
DepthFSearch(G,w,visited,Visit);//递归
w = GetNextVex(G,v,w); //取下一个邻接顶点
}
}
//非连通图的深度优先遍历函数
void DepthFirstSearch(AdjMGraph G , void Visited(DataType item)){
//非连通图访问操作为Visit()的深度优先遍历
int i;
int *visited = (int *)malloc(sizeof(int)*G.Vertices.size);
for(i = 0 ; i < G.Vertices.size ; i++)
visited[i] = 0; //访问标记初始化为0
for(i = 0 ; i < G.Vertices.size ; i++)
if(!visited[i])
DepthFSearch(G , i , visited , Visit); //以每个顶点为初始顶点进行调用
free(visited);
}
//连通图的广度优先遍历函数
void BoradFSearch(AdjMGraph G , int v , int visited[] , void Visit(DataType item)){
//连通图G以v为初始顶点的、访问操作为Visit()的广度优先遍历
int u , w;
SeqCQueue queue;
Visit(G.Vertices.list[v]); //访问顶点v
visited[v] = 1; //将顶点v置为已访问标记
QueueInitiate(&queue);
QueueAppend(&queue , v); //入队列
while(QueueNotEmpty(queue)){ //当队列非空时
QueueDelete(&queue , &u); //出队列
w = GetFirstVex(G , u); //取顶点u的第一个邻接顶点
while(w != -1){
if(!visited[w]){ //若顶点w没有被访问过
Visit(G.Vertices.list[w]); //访问顶点w
visited[w] = 1; //将顶点w置为已访问标记
QueueAppend(&queue,w); //顶点w入队列
}
w = GetNextVex(G , u , w); //取下一个邻接顶点
}
}
}
//非连通图的广度优先遍历函数
void BoradFirstSearch(AdjMGraph G , void Visit(DataType item)){
int i;
int *visited = (int *)malloc(sizeof(int)*G.Vertices.size);
for(i = 0 ; i < G.Vertices.size ; i++)
visited[i] = 0; //访问标记初始化为0
for(i = 0 ; i < G.Vertices.size ; i++)
if(!visited[i])
BoradFSearch(G , i , visited , Visit); //以每个顶点为初始顶点进行调用
free(visited);
} AdjMGraphCreate.h
//AdjMGraphCreate.h
//用邻接矩阵创建图G
typedef struct{
int row;
int col;
int weight;
}RowColWeight;
void CreateGraph(AdjMGraph *G , DataType V[] , int n , RowColWeight E[] , int e){
int i , k;
Initiate(G , n); //顶点顺序表初始化
for(i = 0 ; i < n ; i++)
InsertVertex(G , V[i]); //插入顶点
for(k = 0 ; k < e ; k++)
InsertEdge(G , E[k].row , E[k].col , E[k].weight);//插入边
}AdjLGraph.h
//AdjLGraph.h
//邻接链表作为储结构存储图G
#include<stdio.h>
#include<stdlib.h>
#define MaxVertices 10
typedef char DataType;
typedef struct Node{
int dest; //邻接边的弧头顶点序号
struct Node *next; //单链表的下一个结点指针
}Edge; //邻接边单链表的结点结构体
typedef struct{
DataType data; //顶点数据元素
int source; //邻接边的弧尾顶点序号
Edge *adj; //邻接边的头结点
}AdjLHeight; //数组的数据元素类型结构体
typedef struct{
AdjLHeight a[MaxVertices]; //邻接表数组
int numOfVerts; //顶点个数
int numOfEdges; //边个数
}AdjLGraph; //邻接表结构体
//初始化图G AdjInitiate(AdjLGraph *G)
void AdjInitiate(AdjLGraph *G){
int i;
G->numOfEdges = 0;
G->numOfVerts = 0;
for(i = 0 ; i < MaxVertices ; i++){
G->a[i].source = i; //置邻接边的弧头顶点序号
G->a[i].adj = NULL; //置邻接边单链表头指针初值为0
}
}
//插入顶点 InsertVertex(AdjLGraph *G , int i , DataType vertex)
void InsertVertex(AdjLGraph *G , int i , DataType vertex){
//在图G中的第i(0<=i<MaxVertices)个位置插入顶点数据元素vertex
if(i >= 0 && i < MaxVertices){
G->a[i].data = vertex; //存储顶点数据元素vertex
G->numOfVerts++;
}
else printf("顶点越界!\n");
}
//插入边
void InsertEdge(AdjLGraph *G , int v1 , int v2){
//在图G中加入边<v1,v2>
Edge *p;
if(v1<0 || v1>=G->numOfVerts || v2<0 || v2>=G->numOfVerts){
printf("参数v1或v2越界出错!\n");
return ;
}
p = (Edge *)malloc(sizeof(Edge)); //申请邻接边单链表结点空间
p->dest = v2; //置邻接边弧头序号
p->next = G->a[v1].adj; //新结点插入单链表的表头
G->a[v1].adj = p; //头指针指向新的单链表头
G->numOfEdges++;
}
//删除边
void DeleteEdge(AdjLGraph *G , int v1 , int v2){
//删除图G中的边<v1,v2>
Edge *curr , *pre;
if(v1<0 || v1>=G->numOfVerts || v2<0 || v2>=G->numOfVerts){
printf("参数v1或v2越界出错!\n");
return ;
}
pre = NULL;
curr = G->a[v1].adj;
while(curr != NULL && curr->dest != v2){
//在v1顶点的邻接边单链表中查找v2顶点
pre = curr;
curr = curr->next;
}
//删除邻接边<v1,v2>
if(curr != NULL && curr->dest == v2 && pre == NULL){
//当邻接边<v1,v2>的结点是单链表的第一个结点时
G->a[v1].adj = curr->next;
free(curr);
G->numOfEdges--;
}
else if(curr != NULL && curr->dest == v2 && pre != NULL){
//当邻接边<v1,v2>的结点不是单链表的第一个结点时
pre->next = curr->next;
free(curr);
G->numOfEdges--;
}
else printf("边<v1,v2>不存在!\n");
}
//取第一个邻接顶点
int GetFirstVex(AdjLGraph G , int v){
//取图G中顶点v的第一个邻接顶点
//若取到,返回顶点对应序号,否则返回-1
Edge *p;
if(v < 0 || v >= G.numOfVerts){
printf("参数v1或v2越界出错!\n");
return -1;
}
p = G.a[v].adj;
if(p != NULL) return p->dest;
else return -1;
}
//取下一个邻接顶点
int GetNextVex(AdjLGraph G , int v1 , const int v2){
//取图G中顶点v1的邻接顶点v2的下一个邻接顶点
//若取到,则返回该邻接顶点的对应序号,否则返回-1
Edge *p;
if(v1 < 0 || v1 >= G.numOfVerts || v2 < 0 || v2 >= G.numOfVerts){
printf("参数v1或v2越界出错!\n");
return -1;
}
p = G.a[v1].adj;
while(p != NULL){
if(p->dest != v2){
p = p->next;
continue;
}
else break;
}
p = p->next;
if(p != NULL) return p->next->dest;
else return -1;
}
//撤销申请空间
void AdjDestroy(AdjLGraph *G){
//撤销图G中的所有单链表占用的存储空间
int i;
Edge *p , *q;
for(i = 0 ; i < G->numOfVerts ; i++){
p = G->a[i].adj;
while(p != NULL){
q = p->next;
free(p);
p = q;
}
} }AdjLGraphCreate.h
//AdjLGraphCreate.h
//用邻接链表创建图G
void CreateGraph(AdjLGraph *G , DataType v[] , int n , RowColWeight d[] , int e){
//创建有n个顶点e条边的图 G
//顶点信息存放在数组v中,边的信息存放在数组d中
int i , k;
AdjInitiate(G); //初始化
for(i = 0 ; i < n ; i++) //插入顶点
InsertVertex(G , i , v[i]);
for(k = 0 ; k < e ; k++) //插入边
InsertEdge(G , d[k].row , d[k].col);
} 
魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)