目录

12.1.概述

12.1.1.无权图的最短路径

 12.1.2.带权图的最短路径

1.单源最短路径

2.多源最短路径

12.2.代码实现

---

12.1.概述

12.1.1.无权图的最短路径

无权图的最短路径，即最少步数，使用BFS+贪心算法来求解最短路径，比较好实现，此处不做展开讨论。

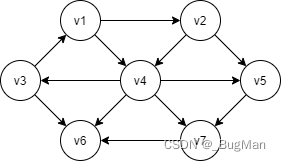
 12.1.2.带权图的最短路径

有权图的最短路径，不考虑权重为负数的情况，因为权重为负数的情况极有可能出现负值圈，在这个圈子上形成环路，最短路径是无限兜圈，趋于负无穷。

所以此处我们只考虑权重不为负数的带权图的最短路径求解问题。带权图的最短路径求解问题主要求两种最短路径：

• 单源最短路径，某个点到全图各点之间的最短路径。
• 多源最短路径，遍历全图的最短路径。

单源最短路径用Dijkstra算法求解，多源最短路径用Floyd算法求解。

1.单源最短路径

单源最短路径用Dijkstra算法求解，Dijkstra算法其本质是个贪心算法。整个过程就是选择局部最优解，组成最后的解。

以下展示一个Dijkstra求解v1的单源最短路径的过程：

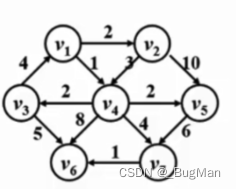
 记录两个值：

distance，到某个结点的最短距离，初始化值为无穷大，表示暂时未记录。

route，全局最短路径，初始化值为-1，表示暂时未记录。

下标	1	2	3	4	5	6	7
distance	无穷大	无穷大	无穷大	无穷大	无穷大	无穷大	无穷大
route	-1	-1	-1	-1	-1	-1	-1

 v1开始，刷新distance和route的值：

v1—>v1，distance为0

v1—>v2，distance为2<∞，将2刷新为v1—>v2的最短距离，将1（指代v1）刷新为最短路径。

v4同理……

下标	1	2	3	4	5	6	7
distance	0	2	无穷大	1	无穷大	无穷大	无穷大
route	-1	1	-1	1	-1	-1	-1

扫描distance表发现distance最小的v4，于是将v4上得到的数据刷新进distance和route：

下标	1	2	3	4	5	6	7
distance	0	2	3	1	3	9	5
route	-1	1	4	1	4	4	4

一直重复上面步骤，直到图里所有结点都被遍历一次，会得到如下结果：

下标	1	2	3	4	5	6	7
distance	0	2	3	1	3	6	5
route	-1	1	4	1	4	7	4

distance记录的是v1到每个结点的最短路径，route里面记录的最大值是全局遍历一遍的最短路径。

2.多源最短路径

多源最短路径用floyd算法求解，多源最短路径不能只关注于当前最优解，还要关注全局最优解，求解此类问题一般使用动态规划，floyd算法就是个求解多源最短路径的经典动态规划算法。本文主要论述Dijkstra算法，floyd算法暂时不展开。

12.2.代码实现

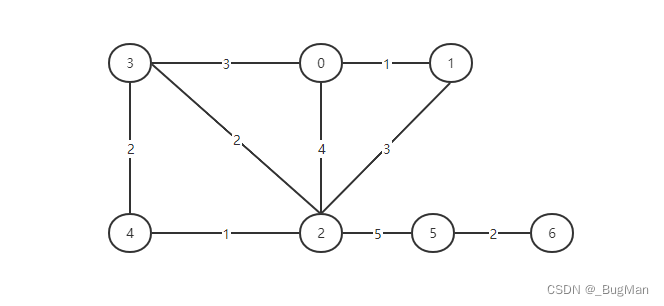
以遍历如下无向图为例（为什么不遍历上面的例子喃？因为代码是很久前写的了。上面的例子是写文的时候新写的，偷个懒不想改代码了~嘿嘿）：

public class Dijkstra {
    static int[][] graph;
    static int[] dist;
    static int[] path=new int[7];
    static boolean[] isUsed=new boolean[7];
    static {
        graph=new int[][]{
                {0,1,4,3,0,0,0},
                {1,0,3,0,0,0,0},
                {4,3,0,2,1,5,0},
                {3,0,2,0,2,0,0},
                {0,0,1,2,0,0,0},
                {0,0,5,0,0,0,2},
                {0,0,0,0,0,2,0}
        };
        dist=new int[]{Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE};
    }
    public static void dijkstra(){
        while(true){
            //判断节点是否已经全部纳入
            if(isOver()){
                break;
            }
            //寻找未纳入的dist最小节点
            int i=findMin();
            //设置为已遍历状态
            isUsed[i]=true;
            //遍历该节点邻接节点
            for (int j=0;j<graph[i].length;j++) {
                if(graph[i][j]!=0&&isUsed[j]==false){
                    //更新dist、path
                    flashDistAndPath(i,j);
                }
            }
        }
    }

    public static int findMin(){
        int min=Integer.MAX_VALUE;
        int index=-1;
        for(int i=0;i<dist.length;i++){
            if(min>dist[i]&&isUsed[i]==false){
                min=dist[i];
                index=i;
            }
        }
        return index;
    }

    //之前的dist值一定是之前该节点到根节点的最短路径开销
    public static void flashDistAndPath(int i,int j){
            if(isUsed[j]==false) {
                if (graph[i][j] + dist[i] < dist[j]) {
                    dist[j] = graph[i][j] + dist[i];
                    path[j] = j;
                }
            }
    }

    public static boolean isOver(){
        int trues=0;
        for (boolean isused:isUsed) {
            if(isused==true){
                trues++;
            }
        }
        if(trues==dist.length){
            return true;
        }
        return false;
    }

    public static void main(String[] args) {
        isUsed[0]=true;
        dist[1]=1;
        dist[2]=4;
        dist[3]=3;

        path[1]=0;
        path[2]=0;
        path[3]=0;
        dijkstra();
        for (int i=0;i<dist.length;i++){
            System.out.println(dist[i]);
        }
    }
}