数据结构

在计算机科学中

• 数据：是对客观事物的符号表示，是能输入到计算机并被计算机程序处理的符号的总称。
• 数据元素：是数据的基本单位，在计算机程序中通常作为一个整体进行考虑和处理。
• 数据项：一个数据元素由若干个数据项组成，数据项是构成数据的最小单位。
• 数据对象：是具有相同性质的数据元素的集合（强调的是数据元素性质的相同）。

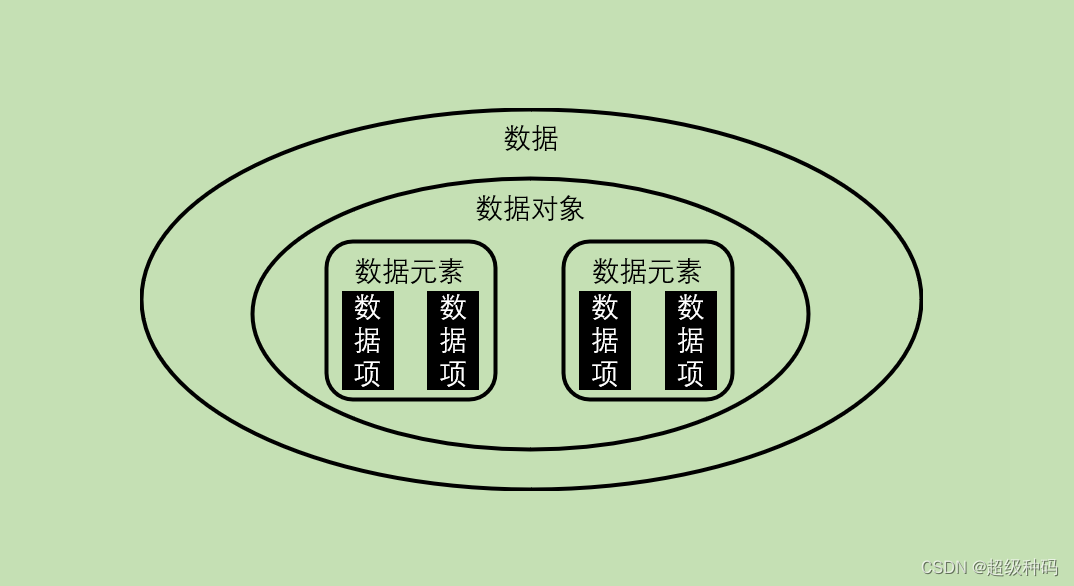
• 数据结构：是相互之间存在一种或多种特定关系的数据元素的集合（强调的是数据元素之间的关系）。数据结构的三要素是逻辑结构、存储结构和数据运算：

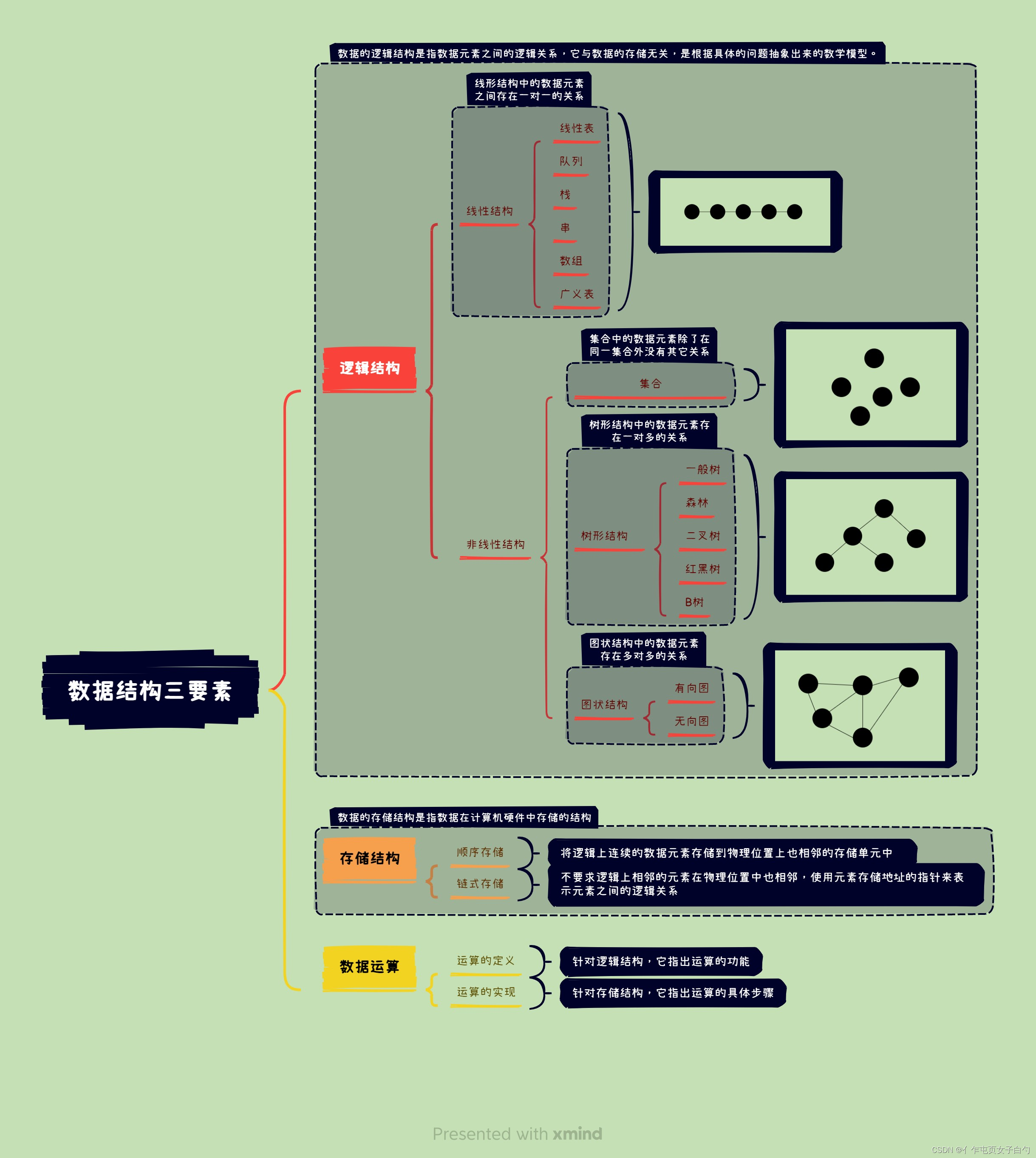
上图中存储结构是依据数据在物理存储器上存储的位置进行描述的，如果在高级语言（如C语言）层面上进行描述，那么可以使用数组类型来描述顺序存储结构、用指针来描述链式存储结构。

• 数据类型：数据类型是一个值的集合和定义在此集合上的一组操作的总称。
  • 原子类型：其值不可再分的数据类型
  • 结构类型：其值可以分解为若干成分的数据类型。
• 抽象数据类型：是抽象数据组织及与之相关的操作。

算法

算法是为求解一个问题需要遵循的、被清楚指定的有限指令集合。一个算法具有以下五个特性：

• 有穷性：一个算法必须在执行有穷步之后结束，且每一步都在有穷时间内完成。
• 确定性：算法中的每一条指令都必须有明确的含义，没有二义性，对相同的输入只能得到相同的输出。
• 可行性：算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现。
• 输入：一个算法有零个或多个输入。
• 输出：一个算法有一个或多个输出。

一个算法的设计取决于所选定的逻辑结构，而算法的实现依赖于所采用的存储结构。

算法分析

一旦给定一个算法并且确认其是正确的，那么重要的一步就是对这个算法进行算法分析，算法分析主要考虑算法的效率，算法效率包含以下两方面：

• 时间效率：指算法所消耗的时间，用时间复杂度来度量。
• 空间效率：指算法执行过程中所消耗的存储空间。用空间复杂度来度量。

时间复杂度

一个算法运行的时间大致可以等于计算机执行算法指令的时间（$t$）与指令执行次数（$s$）的乘积。
$$T(n)=\sum _{i=1}^n{t}_i\times s_i$$

由于每个指令执行的时间由计算机的硬件和软件条件决定，和算法本身没有关系，因此可以将每个指令执行的时间可以看作一个单位时间，那么讨论算法执行时间的问题就变成了讨论算法执行频度的问题：

$$T(n)=\sum _{i=1}^n{s}_i$$

下面分析一下选择排序算法的执行频度：

public static void selectionSort(int []data){
    for (int i = 0; i < data.length-1; i++) { //n次
        int minIndex=i; //n-1次
        for (int j = i+1; j < data.length; j++) { //n(n-1)/2次
            if (data[j]<data[minIndex]){ //n(n-2)/2次
                minIndex=j; //n(n-2)/2次
            }
        }
        int temp=data[i]; //n-1次
        data[i]=data[minIndex]; //n-1次
        data[minIndex]=temp; //n-1次
    }
}

所以选择排序的执行频度为：
$$T(n)=3n^2÷2+5n÷2-4$$

但是这一过程也相当的繁琐并且结果难以比较，由公式
$$\underset{x\to \infty }{\lim }\frac{a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0}{b_m{x}^m+b_{m-1}{x}^{m-1}+\cdots +b_{1}x+b_0}=\{\begin{array}{l}\frac{a_n}{b_m},n=m\\ 0,n<m\\ \infty ,n>m\end{array}$$
可知，如果存在一个函数$f(n)$，使$$\underset{n\to \infty }{\lim }\frac{T(n)}{f(n)}=C(C\ne 0)$$那么$f(n)$和$T(n)$就是同阶的，记作$T(n)=O(f(n))$，$O(f(n))$就称为算法的时间复杂度。那么上述选择排序的时间复杂度就为$O(n^2)$。也就是说在寻找算法频度时不需要找出所有语句执行的频度，只需要找出对算法频度贡献最大的语句即可。此外，输入数据的性质会影响算法的执行频度，在这种情况下将算法的时间复杂度分为三种：

• 最坏时间复杂度：输入数据的性质使算法的执行频度很高。
• 平均时间复杂度：输入数据的性质使算法的执行频度很平均。
• 最好时间复杂度：输入数据的性质使算法的执行频度很低。

但一般只考虑最坏时间复杂度，以保证算法的运行时间不会比它更长。在计算程序的时间复杂度时，有以下两条规则：

• 加法原则：$T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))$
• 乘法原则：$T(n)=T_1(n)\times T_2(n)=O(f(n))\times O(g(n))=O(f(n)\times Og(n))$

常见时间复杂度的关系为：
$$O(1)<O(lo{g}_{2}n)<O(n)<O(nlo{g}_{2}n)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)$$

空间复杂度

与时间复杂度类似，算法的空间复杂度记作：
$$S(n)=O(f(n))$$

它包括算法本身要占据的空间以及使用的辅助空间。在计算空间复杂度时只需要计算辅助空间即可，比如上述的选择排序算，它仅需要一个临时变量作为辅助空间，所以它的空间复杂度为$O(1)$，当算法的空间复杂度为$O(1)$时称它在原地工作。注意，当函数递归调用时，要考虑每一次递归使用的辅助空间。