拓扑排序是一种对有向无环图（DAG）的顶点进行线性排序的算法，使得对于每一条有向边 u→v，顶点 u 总在 v 之前，有环的图不会有拓扑序列。这是比较书面的，本质上就是输出入度为0的点，而随着添加了新的点A，我们原图当中的点数就减少，那么以A为起点的边的终点的入度就会-1，以此类推，入度为0的点就会增加，原图当中的点数减少直至为0个

1.bfs怎么实现

理解：这种方法的思路和定义是对应的，就是一步步找入度为0的点。我们确定一下会用到哪些数据结构，首先存图时，我们使用链式前向星（其他方法也行，代码跟着变通就好）；另外，我们的目标是找入度为0的点，用一个整型数组ind来记录每个点的入度, 因为是基于bfs的，所以我们还要用队列来存这些拓扑序列中的顶点

第一步：先遍历ind数组，找到入度为0的点加入拓扑序列的起点

for(int i=1;i<=n;i++) {
			if(ind[i]==0)ans.add(i);
}

接下来就开始进行遍历了

注意：设当前出队顶点为A,在for循环中，我们遍历所有以他为起点的边，并将这些边的终点对应的入度值-1，那么这些顶点的入度值之前就为1，现在减去值就为0，所以加上判断语句是这些入度为0的点入队

while(!ans.isEmpty()) {
			int topp=ans.peek();
			ans.poll();
			System.out.print(topp+" ");
			for(int i=head[topp];i<=m&&i!=-1;i=edges[i].nextt) {
				int e=edges[i].to;
				ind[e]--;
				if(ind[e]==0) {
					ans.add(e);//如果入度为0，就加入拓扑序列
				}
			}
}

对于这种方法，是可以用来判断该图中是否有环的

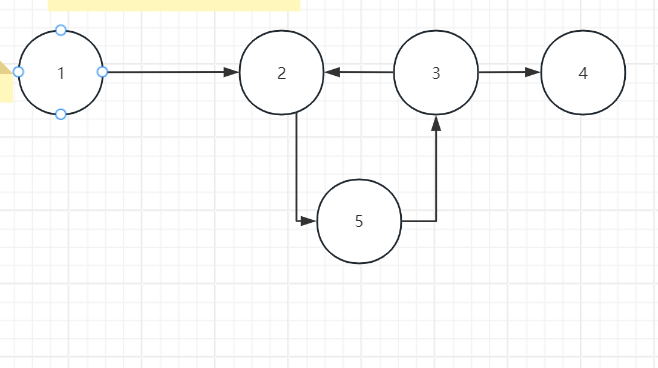
下图为例，当我们把1加入，并出队后，图中剩下2，3，4，5这些点，并构成了一个有向的有环图

，发现此时图中根本没有入度值为0 的点，那么队列没法加入新的点，所以遍历到这儿就结束了，

所以我们可以根据输出点数判断是否有环，仅当输出点数=n时说明无环，可以得到拓扑序列

bfs算法完整代码

import java.util.*;
public class topo_bfs {
	//使用链式前向星存图
	//只有DAG(有向无环图)才有拓扑序列
	static int n,m;
	static class Edge{
		int nextt;
		int to ;
	}
	static Edge[]edges=new Edge[1005];
	static int[] head=new int[105];
	static int[] ind=new int[105];//记录每个顶点的入度
	static Queue<Integer> ans=new LinkedList<>();
	public static void topo() {
		
		for(int i=1;i<=n;i++) {
			if(ind[i]==0)ans.add(i);
		}
		//出队，并将出队元素的邻接顶点的入度减1
		while(!ans.isEmpty()) {
			int topp=ans.peek();
			ans.poll();
			System.out.print(topp+" ");
			for(int i=head[topp];i<=m&&i!=-1;i=edges[i].nextt) {
				int e=edges[i].to;
				ind[e]--;
				if(ind[e]==0) {
					ans.add(e);//如果入度为0，就加入拓扑序列
				}
			}
		}
	}
	public static void main(String[] args) {
		
		Scanner sc=new Scanner(System.in);
		n=sc.nextInt();
		m=sc.nextInt();
		Arrays.fill(head, -1);
		int s,e;
		//存图
		for(int i=1;i<=m;i++) {
		edges[i]=new Edge();
		s=sc.nextInt();
		e=sc.nextInt();
		edges[i].to=e;
		ind[e]++;
		edges[i].nextt=head[s];
		head[s]=i;
		}
		topo();
	}

}
/*样例
有向无环图
5 5
1 2
2 4
3 2
3 4
4 5

有向有环图
5 5
1 2
2 5
5 3
3 2
3 4
*/

2.dfs怎么实现

理解：这种方法是基于逆拓扑的想法，就是找出度为0的点。可以这样来想：当进行dfs的时候，是不是总会从起点出发，遍历到最后一个节点end，而且end后面肯定就没有点了，那么它的出度就为0，刚好是我们需要的，所以就可以利用dfs了

使用到的数组结构：存图-链式前向星，flagg数组记录访问信息，用栈存拓扑序列（为什么是栈后面会解释）

问题1：当从一个顶点出发不能遍历完整个图怎么办

像这样，如果我们从1出发，只能遍历到1，2，4，5

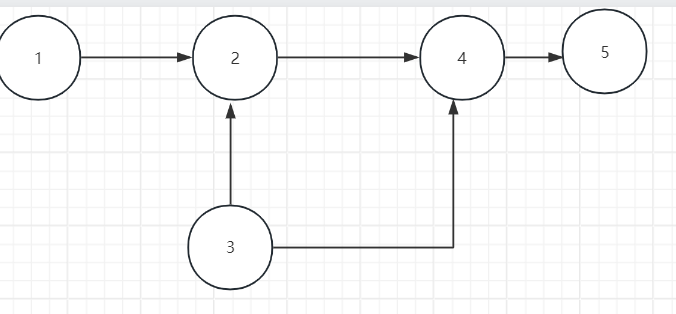
解决：使用循环，遍历所有顶点作为起点进行dfs

for(int i=1;i<=n;i++) {
					//不同起点开始对应的拓扑序列不同，而且由于不是强连通，任意两点不能相互可达
					//所以使用for循环遍历
					dfs(i);
					if(flagg[i]==2) {
						System.out.println("有环，无拓扑序列");
						ifcircle=true;
						break;
					}
}

关于dfs的部分涉及到递归确实不好解释

我们来看图，先看左边了解一下flagg的作用

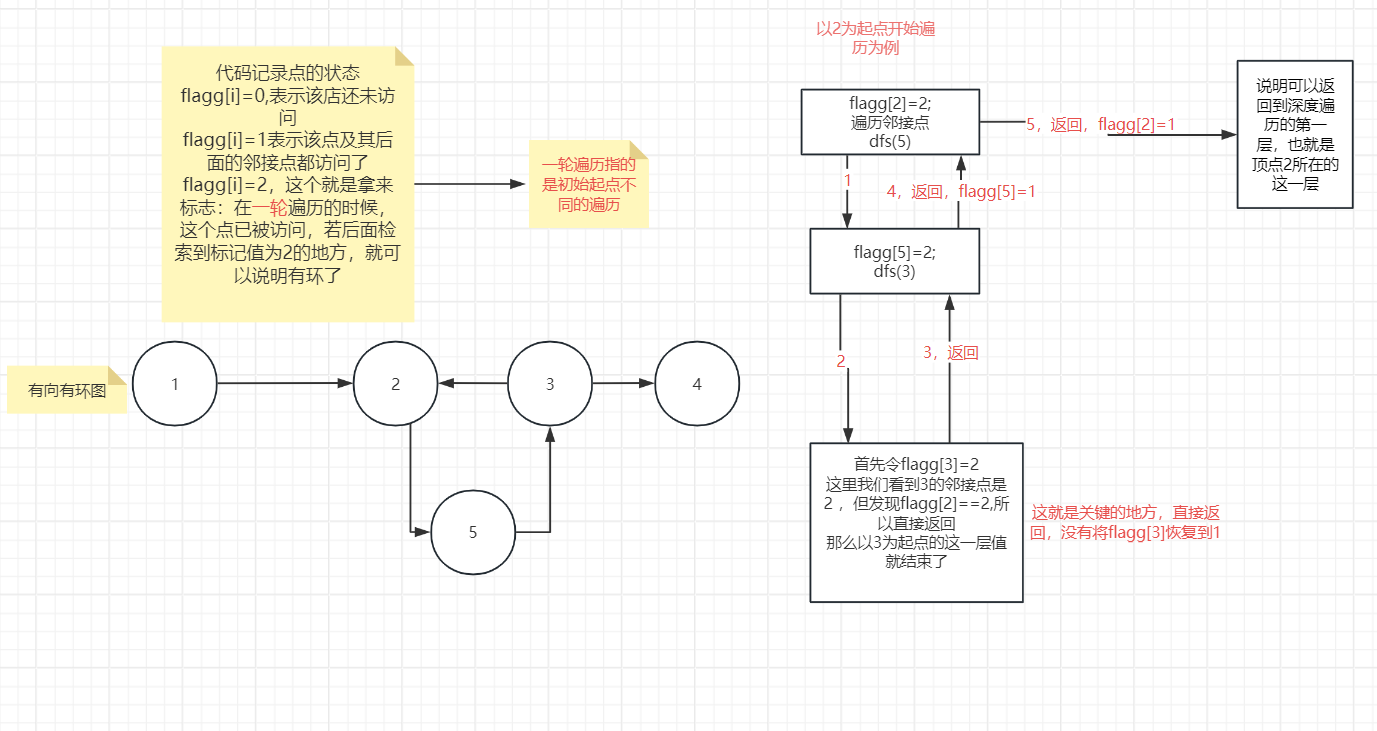
没有判环的代码

import java.util.*;

public class topo_dfs {
	static int n,m;
	static class Edge{
		int nextt;
		int to ;
	}
	static Edge[]edges=new Edge[1005];
	static int[] head=new int[105];
	static int[]flagg=new int[105];
	static Stack<Integer>ans=new Stack<>();
	public static void dfs(int start) {
		if(flagg[start]==0) {
			flagg[start]=1;
		}else return;
		for(int i=head[start];i<=m&&i!=-1;i=edges[i].nextt) {
			int e=edges[i].to;
			if(flagg[e]==0) {
				dfs(e);
			}
		}
		//遍历所有邻接点后自己入栈
		ans.push(start);
		
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner sc=new Scanner(System.in);
		n=sc.nextInt();
		m=sc.nextInt();
		Arrays.fill(head, -1);
		int s,e;
		//存图
		for(int i=1;i<=m;i++) {
		edges[i]=new Edge();
		s=sc.nextInt();
		e=sc.nextInt();
		edges[i].to=e;
		edges[i].nextt=head[s];
		head[s]=i;
		}
		for(int i=1;i<=n;i++) {
			//不同起点开始对应的拓扑序列不同，而且由于不是强连通，任意两点不能相互可达
			//所以使用for循环遍历
			dfs(i);
		}
		while(!ans.isEmpty()) {
			int topp=ans.peek();
			ans.pop();
			System.out.print(topp+" ");
		}

	}

}
/*样例
有向无环图
5 5
1 2
2 4
3 2
3 4
4 5

//有向有环图
5 5
1 2
2 5
5 3
3 2
3 4
*/

解释：其实我们平常情况下直接回想flagg=0或1两个值就够了，但是因为我写的有判环部分，所以有3个值，如果想看不判环的代码，参考上面

判环代码

import java.util.Arrays;
import java.util.Scanner;
import java.util.Stack;

import template.topo_dfs.Edge;

public class topo_dfs1 {
	static int n,m;
	static class Edge{
		int nextt;
		int to ;
	}
	static Edge[]edges=new Edge[1005];
	static int[] head=new int[105];
	static int[]flagg=new int[105];
	static Stack<Integer>ans=new Stack<>();
	public static void dfs(int start) {
		//有环的本质就是从起点又回到了起点
		if(flagg[start]==2||flagg[start]==1)return;
		flagg[start]=2;
		
		for(int i=head[start];i<=m&&i!=-1;i=edges[i].nextt) {
			int e=edges[i].to;
			if(flagg[e]==2)return;
			else if(flagg[e]==0) {
				dfs(e);
			}
		}
		
		//如果有环，那么在if判断的时候就结束了遍历，就不能恢复
		
		flagg[start]=1;//恢复
		
		//遍历所有邻接点后自己入栈
		
		ans.push(start);
		
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
				Scanner sc=new Scanner(System.in);
				n=sc.nextInt();
				m=sc.nextInt();
				boolean ifcircle=false;
				Arrays.fill(head, -1);
				int s,e;
				//存图
				for(int i=1;i<=m;i++) {
				edges[i]=new Edge();
				s=sc.nextInt();
				e=sc.nextInt();
				edges[i].to=e;
				edges[i].nextt=head[s];
				head[s]=i;
				}
				for(int i=1;i<=n;i++) {
					//不同起点开始对应的拓扑序列不同，而且由于不是强连通，任意两点不能相互可达
					//所以使用for循环遍历
					dfs(i);
					if(flagg[i]==2) {
						System.out.println("有环，无拓扑序列");
						ifcircle=true;
						break;
					}
				}
				for(int i=1;i<=n;i++)
					System.out.print(flagg[i]+" ");
				while(!ifcircle&&!ans.isEmpty()) {
					int topp=ans.peek();
					ans.pop();
					System.out.print(topp+" ");
				}
				
	}

}
/*样例
有向无环图
5 5
1 2
2 4
3 2
3 4
4 5

//有向有环图
5 5
1 2
2 5
5 3
3 2
3 4
*/

问题2：为什么要用栈？

我们使用深度优先遍历，遍历的终点（出度为0）是最后一层元素，这也是为什么我们想到逆拓扑

那么现在我们要求拓扑序列，所以就应该倒序输出，就想到了用栈，其实用队列和数组也可以，只

是在输出上处理一下就好了

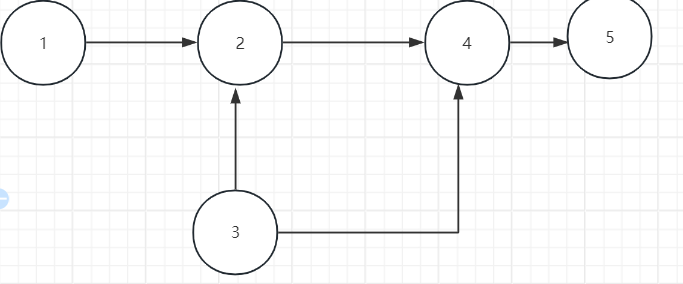
问题3：如果不从1开始遍历会不会有问题？

设想一下，如果我们是以下图中的1开始遍历那么调用dfs(1)的时候，栈中序列就是（栈顶->栈底）：1 2 4 5

如果我们是从4开始遍历呢 ？栈中序列就是（栈顶->栈底）4 5

发现了吗，其实从谁开始都没有问题，因为每个顶点都会经历一次dfs而每次处理后栈中序列的相对位置不会变化就像这里的5和4，该在前面的都会在前面，该在后面的也在后面