武汉理工大学-数据结构与算法-(3)二叉树与哈夫曼树
实验1:树的遍历、叶节点数量的计算、深度的计算实验目标选择合适的结构存储树,编写程序,实现对该树的遍历、叶节点数量的计算、深度的计算。存储结构本实验采用 二叉树型 (孩子-兄弟) 结构 存储://树的结点(二叉树模式存储)typedef struct Node {ElemType data;//数据Node *child;//孩子指针Node *br...
文章目录
实验1:树的遍历、叶节点数量的计算、深度的计算
实验目标
选择合适的结构存储树,编写程序,
实现对该树的遍历、叶节点数量的计算、深度的计算。
存储结构
本实验采用 二叉树型 (孩子-兄弟) 结构 存储:
//树的结点(二叉树模式存储)
typedef struct Node {
ElemType data; //数据
Node *child; //孩子指针
Node *brother; //兄弟指针
}Node;
//树结构体
struct Tree {
int Leaves = 0; //树的叶节点数
int depth = 0; //树的深度
Node Nodes[MAX_TREE_SIZE + 1]; //树结点数组(0号不使用)
}Tree;
首先引入一个重要的定理:任意一棵普通树 (不一定是二叉树) ,都可以唯一地转化为一棵二叉树来表示。
因此,我们可以将所有的树结构统一转化为二叉树进行表示,对二叉树进行各种操作与计算,简化代码的编写难度。
转化的规则如下:
最左孩子作为左子树(对应 Node *child 孩子指针),右侧第一个兄弟作为右子树(对应 Node *brother 兄弟指针)。
例如下图所示,左图为转化前的普通树型结构,右图为转化后的二叉树型结构: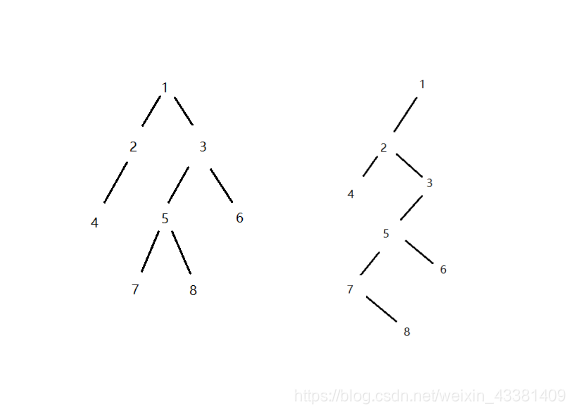
树的遍历
由于采用了二叉树型的结构进行存储,可使用二叉树的三种遍历方法:先序遍历、中序遍历、后序遍历。
//先序遍历
bool PreOrderTraverse(Node *T, bool(*Visit)(Node *T))
{
if (T) {
if (Visit(T)) {
if (PreOrderTraverse(T->child, Visit)) {
if (PreOrderTraverse(T->brother, Visit))
return true;
}
}
return false;
}
else
return true;
}
//中序遍历
bool InOrderTraverse(Node *T, bool(*Visit)(Node *T))
{
if (T) {
if (InOrderTraverse(T->child, Visit)) {
if (Visit(T)) {
if (InOrderTraverse(T->brother, Visit))
return true;
}
}
return false;
}
else
return true;
}
//后序遍历
bool PostOrderTraverse(Node *T, bool(*Visit)(Node *T))
{
if (T) {
if (PostOrderTraverse(T->child, Visit)) {
if (PostOrderTraverse(T->brother, Visit)) {
if (Visit(T))
return true;
}
}
return false;
}
else
return true;
}
遍历的 Visit 函数采用 PrintElem 函数进行结点信息打印:
//打印数据
bool PrintElem(Node *T)
{
cout << T->data << " ";
return true;
}
该部分属于二叉树基本知识,此处采用 递归 方法进行编写。
叶节点数量的计算
叶节点数量的计算可以通过 遍历 + 判断是否为叶节点 两步骤的组合进行。
只需将遍历的 Visit 函数替换成 PrintLeaves 函数进行逐个结点进行判断即可:
//判断并打印叶结点
bool PrintLeaves(Node *T)
{
if (T->child == NULL) {
cout << T->data << " ";
Tree.Leaves++;
}
return true;
}
判断叶节点的依据是结点没有任何孩子,在二叉树型结构表示为没有左子树。
深度的计算
本文采用递归方法计算深度:
//递归计算树的深度
int GetDepth(Node *T)
{
//左右分支的深度
int left, right;
//除非没有子结点, 否则延伸下去深度+1
if (T->child == NULL) left = 1;
else left = GetDepth(T->child) + 1;
//右分支为兄弟结点, 延伸深度不变
if (T->brother == NULL) right = 1;
else right = GetDepth(T->brother);
//返回左右深度最大值
return left > right ? left : right;
}
递归过程由树的底端向上进行:最初将 最底端结点标记为1,每个父结点标记均为子节点标记+1 ,以此类推。
注意 只有经过左分支向上延伸才+1,经过右分支标记不变 。所得根结点标记即为整棵树的深度。
源代码整合
#define MAX_TREE_SIZE 100 //树结构最大结点数
#define ElemType int //数据类型
#include <iostream>
using namespace std;
//树的结点(二叉树模式存储)
typedef struct Node {
ElemType data; //数据
Node *child; //孩子指针
Node *brother; //兄弟指针
}Node;
//树结构体
struct Tree {
int Leaves = 0; //树的叶节点数
int depth = 0; //树的深度
Node Nodes[MAX_TREE_SIZE + 1]; //树结点数组(0号不使用)
}Tree;
//打印数据
bool PrintElem(Node *T)
{
cout << T->data << " ";
return true;
}
//判断并打印叶结点
bool PrintLeaves(Node *T)
{
if (T->child == NULL) {
cout << T->data << " ";
Tree.Leaves++;
}
return true;
}
//先序遍历
bool PreOrderTraverse(Node *T, bool(*Visit)(Node *T))
{
if (T) {
if (Visit(T)) {
if (PreOrderTraverse(T->child, Visit)) {
if (PreOrderTraverse(T->brother, Visit))
return true;
}
}
return false;
}
else
return true;
}
//中序遍历
bool InOrderTraverse(Node *T, bool(*Visit)(Node *T))
{
if (T) {
if (InOrderTraverse(T->child, Visit)) {
if (Visit(T)) {
if (InOrderTraverse(T->brother, Visit))
return true;
}
}
return false;
}
else
return true;
}
//后序遍历
bool PostOrderTraverse(Node *T, bool(*Visit)(Node *T))
{
if (T) {
if (PostOrderTraverse(T->child, Visit)) {
if (PostOrderTraverse(T->brother, Visit)) {
if (Visit(T))
return true;
}
}
return false;
}
else
return true;
}
//递归计算树的深度
int GetDepth(Node *T)
{
//左右分支的深度
int left, right;
//除非没有子结点, 否则延伸下去深度+1
if (T->child == NULL) left = 1;
else left = GetDepth(T->child) + 1;
//右分支为兄弟结点, 延伸深度不变
if (T->brother == NULL) right = 1;
else right = GetDepth(T->brother);
//返回左右深度最大值
return left > right ? left : right;
}
int main()
{
Tree.Nodes[1] = { 1,&Tree.Nodes[2],NULL };
Tree.Nodes[2] = { 2,&Tree.Nodes[4],&Tree.Nodes[3] };
Tree.Nodes[3] = { 3,&Tree.Nodes[5],NULL };
Tree.Nodes[4] = { 4,NULL,NULL };
Tree.Nodes[5] = { 5,&Tree.Nodes[7],&Tree.Nodes[6] };
Tree.Nodes[6] = { 6,NULL,NULL };
Tree.Nodes[7] = { 7,NULL,&Tree.Nodes[8] };
Tree.Nodes[8] = { 8,NULL,NULL };
//二叉树遍历的三种方法
cout << endl << "先序遍历: " << endl;
PreOrderTraverse(&Tree.Nodes[1], PrintElem);
cout << endl << "中序遍历: " << endl;
InOrderTraverse(&Tree.Nodes[1], PrintElem);
cout << endl << "后序遍历: " << endl;
PostOrderTraverse(&Tree.Nodes[1], PrintElem);
cout << endl;
//遍历叶节点并计算数量
cout << endl << "叶节点: " << endl;
PreOrderTraverse(&Tree.Nodes[1], PrintLeaves);
cout << endl << "叶节点数量: " << endl << Tree.Leaves << endl;
//计算深度
Tree.depth = GetDepth(&Tree.Nodes[1]);
cout << endl << "树的深度: " << endl << Tree.depth << endl;
return 0;
}
树结构可以在 main 函数里进行修改。
运行结果
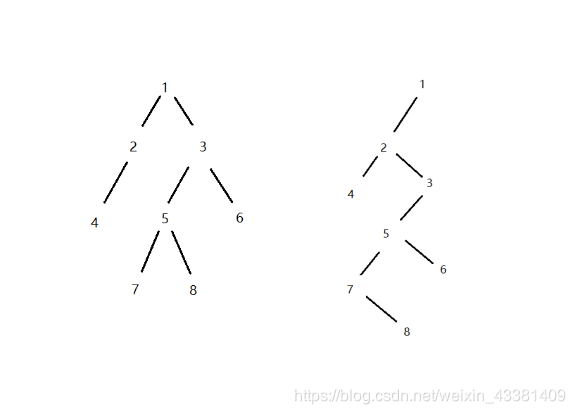
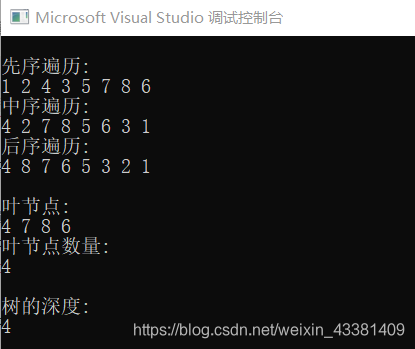
结果如图。
实验2:哈夫曼树的构建
实验目标
给定一组初始权值,编写程序,构建一棵相应的哈夫曼树。
存储结构
//哈夫曼树的结点
typedef struct HTNode {
ElemType weight; //权重
int parent; //父结点序号(由1开始)
int left_child; //左孩结点序号(由1开始)
int right_child; //右孩结点序号(由1开始)
}HTNode;
HTNode nodes[MAX_TREE_SIZE + 1];
哈夫曼树由一个 结点数组 构成,每个结点存有 权值、父结点序号、子节点序号 的信息。
构建流程
首先确定哈夫曼树的结点数量 m=2*n-1,构建长度为 m 的结点数组;赋予初始权值给对应结点,其余结点权值先设为 0。
//创建哈夫曼树
bool CreateHuffmanTree(int *w,int n)
{
//n为初始权重数
if (n <= 1) return false;
//m为哈夫曼树的元素数量
int m = 2 * n - 1;
//前n个存储初始权值
for (int i = 1; i <= n; i++, w++) nodes[i] = { *w,0,0,0 };
for (int i = n + 1; i <= m; i++) nodes[i] = { 0,0,0,0 };
//不断选取最小的两个数
for (int i = n + 1; i <= m; i++) {
int s1, s2;
//在nodes[1~i-1]内选取parent=0且最小的两个权值
Select(i - 1, s1, s2);
//相加并建立父子关系
nodes[s1].parent = i;
nodes[s2].parent = i;
nodes[i].left_child = s1;
nodes[i].right_child = s2;
nodes[i].weight = nodes[s1].weight + nodes[s2].weight;
}
return true;
}
之后需要 从权值中不断选取最小的两个权值,加和后加入权值数组。
//选取最小两个数
void Select(int n, int &s1, int &s2)
{
int min2 = INT_MAX; //倒数第二小的数
int min1 = INT_MAX; //最小的数
for (int i = 1; i <= n; i++) {
if (nodes[i].parent == 0 && nodes[i].weight <= min1) {
min1 = nodes[i].weight;
s1 = i;
}
}
for (int i = 1; i <= n; i++) {
//排除s1 i!=s1
if (nodes[i].parent == 0 && nodes[i].weight <= min2 && i != s1) {
min2 = nodes[i].weight;
s2 = i;
}
}
}
注意每次都选择父结点序号为 0 的权值结点,因为 parent = 0 表示该结点对应权值未被选取过,循环后即可构建出一棵哈夫曼树。
源代码整合
#define MAX_TREE_SIZE 100 //元素最大数量
#define ElemType int //数据类型
#include <iostream>
#include <iomanip>
using namespace std;
//哈夫曼树的结点
typedef struct HTNode {
ElemType weight; //权重
int parent; //父结点序号(由1开始)
int left_child; //左孩结点序号(由1开始)
int right_child; //右孩结点序号(由1开始)
}HTNode;
HTNode nodes[MAX_TREE_SIZE + 1];
//选取最小两个数
void Select(int n, int &s1, int &s2)
{
int min2 = INT_MAX; //倒数第二小的数
int min1 = INT_MAX; //最小的数
for (int i = 1; i <= n; i++) {
if (nodes[i].parent == 0 && nodes[i].weight <= min1) {
min1 = nodes[i].weight;
s1 = i;
}
}
for (int i = 1; i <= n; i++) {
//排除s1 i!=s1
if (nodes[i].parent == 0 && nodes[i].weight <= min2 && i != s1) {
min2 = nodes[i].weight;
s2 = i;
}
}
}
//创建哈夫曼树
bool CreateHuffmanTree(int *w,int n)
{
//n为初始权重数
if (n <= 1) return false;
//m为哈夫曼树的元素数量
int m = 2 * n - 1;
//前n个存储初始权值
for (int i = 1; i <= n; i++, w++) nodes[i] = { *w,0,0,0 };
for (int i = n + 1; i <= m; i++) nodes[i] = { 0,0,0,0 };
//不断选取最小的两个数
for (int i = n + 1; i <= m; i++) {
int s1, s2;
//在nodes[1~i-1]内选取parent=0且最小的两个权值
Select(i - 1, s1, s2);
//相加并建立父子关系
nodes[s1].parent = i;
nodes[s2].parent = i;
nodes[i].left_child = s1;
nodes[i].right_child = s2;
nodes[i].weight = nodes[s1].weight + nodes[s2].weight;
}
return true;
}
int main()
{
//设置初始权值
int w[5] = { 2,3,6,7,8 };
int n = 5;
//建立哈弗曼树
CreateHuffmanTree(w, n);
//打印
for (int i = 1; i <= 2 * n - 1; i++) {
cout << "w[" << i << "]:" << "weight:" << setw(3) << nodes[i].weight << " parent:" << setw(3) << nodes[i].parent
<< " left_child:" << setw(3) << nodes[i].left_child << " right_child:" << setw(3) << nodes[i].right_child << endl;
}
return 0;
}
初始权值可在 main 函数修改。
运行结果
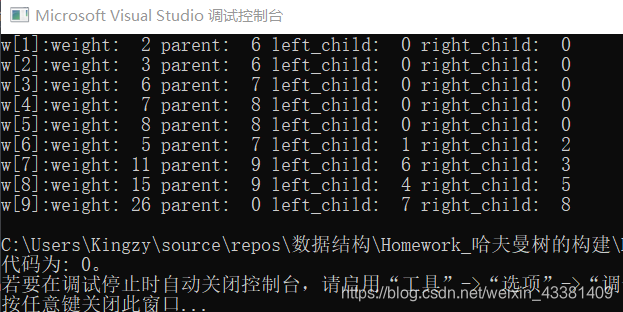
结果如图。
写在最后
声明:本文内容来源于武汉理工大学2019-2020学年数据结构与算法课程实验,仅供学习参考。如有不足地方,还请指出。代码不要无脑抄 ,建议理解思路。祝愿读者能够在编程之路上不断进步!

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)