有需要本项目的代码或文档以及全部资源，或者部署调试可以私信博主

前景引入

随着数据分析浪潮的不断兴起，越来越多的人投身于数据分析领域。相较于其他编程和开发工作，数据分析的入门门槛相对较低，且能够较快地看到成果，因此备受关注。

熟悉数据分析的人通常会先理解业务背景，随后进行数据处理，并思考建模流程，以满足具体的分析需求。在庞大的数据中，由于采集、检测、录入等各环节可能存在误差，常常会出现异常值。异常值可能干扰模型的训练效果以及分析结果的准确性，因此需要进行合理处理。

常见的异常值处理方法包括：删除包含异常值的整行记录，或者对异常值进行标记，交由业务人员进一步核查与判定。

常见的异常值检测方法主要包括统计学方法、基于业务规则的逻辑判断以及基于模型的检测方法等。

IQR（四分位距法）

原理

IQR，全称 Interquartile Range，是一种基于统计分位数的异常检测方法，属于 统计法。

在任何分布中，通常中间 50% 的数据集中在第 25 百分位数（Q1）和第 75 百分位数（Q3）之间。IQR 就是 Q3 - Q1，用于度量数据的集中程度。

IQR 方法的核心逻辑是：

• 正常数据多处于中间区域
• 极端值远离数据中心，超出 IQR 范围

因此，常用下式来检测异常值：

Lower Bound = Q1 - k*IQR
Upper Bound = Q3 + k*IQR

若观测值超出该范围，即认为是异常值。常用 k=1.5，但可根据需求调整。

IQR 的优势是无需假定数据分布是正态分布，对偏态分布也同样适用，属于非参数方法。

方法流程

1. 计算数据的 Q1（25% 分位数）和 Q3（75% 分位数）
2. 计算 IQR = Q3 - Q1
3. 根据阈值 k（通常取 1.5）计算下限、上限
4. 判断数据是否超出范围

优点

• 简单直观，易于实现
• 无需分布假设，适用于非正态分布
• 对极端值不敏感（鲁棒性强）
• 运算非常快，适用于大数据清洗

缺点

• 仅适合单变量分析
• 无法检测多变量或高维空间的异常
• 无法发现局部异常（例如聚类中的局部异常）
• 当异常比例较高时，容易失效
• 阈值 k 的选择较为主观

应用场景

• 数据预处理阶段的初步异常检测
• 财务数据清洗，如检测极端交易额
• 工业传感器单一指标的监测
• 基础统计分析

重要参数

参数名	含义	是否影响检测结果	建议
k	决定异常边界的灵敏度	高	建议 1.5~3，根据业务调整

• k 越小 → 检测更敏感 → 易多报异常
• k 越大 → 检测更保守 → 可能漏检异常

Python 示例

import numpy as np

# 生成示例数据：95% 正常，5% 异常
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])

# 计算分位数
q1 = np.percentile(data, 25)
q3 = np.percentile(data, 75)
iqr = q3 - q1

# 计算上下界
lower_bound = q1 - 1.5 * iqr
upper_bound = q3 + 1.5 * iqr

# 检测异常
outliers = (data < lower_bound) | (data > upper_bound)

print(f"异常值数量：{np.sum(outliers)}")

---

Isolation Forest

原理

Isolation Forest 属于基于树的无监督方法，专门用于检测异常值。
核心思想是：

• 异常值在特征空间中相对孤立，与大部分数据不同
• 随机分割特征空间时，异常值被“孤立”的速度更快

不同于基于距离或密度的方法，Isolation Forest 不计算距离或密度，而是基于树的分割次数：

• 普通样本需要更多的分割才能被孤立
• 异常值通常在少数分割步骤中就被隔离

算法通过平均路径长度衡量异常程度。

方法流程

1. 随机选择一个特征
2. 随机选择分割阈值
3. 重复分割生成树
4. 统计样本在树中的平均路径长度
5. 平均路径短 → 异常；平均路径长 → 正常

优点

• 无需数据分布假设
• 能处理高维数据
• 对大数据友好，复杂度近似线性
• 可并行化
• 自动估计异常比例

缺点

• 存在随机性，结果可能略有波动
• 对 contamination 参数敏感
• 对非常小比例的异常值可能欠检测

应用场景

• 金融欺诈检测
• 网络入侵检测
• 工业设备故障监测
• 高维数据分析

重要参数

参数名	含义	是否影响检测结果	建议
contamination	异常比例，用于确定阈值	高	根据实际场景设置
n_estimators	树的数量	中	默认 100 就够用
max_samples	每棵树使用的样本数（小样本更敏感于异常）	中	通常设 256 或 auto
max_features	每棵树使用的特征数	中	默认 1.0（所有特征）
random_state	随机种子	否	可设定以保证复现

• contamination 是最重要参数，决定检测多少异常

Python 示例

import numpy as np
from sklearn.ensemble import IsolationForest

# 生成示例数据
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])
data = data.reshape(-1, 1)

# 建立模型
model = IsolationForest(contamination=0.05, random_state=42)
outliers = model.fit_predict(data) == -1

print(f"异常值数量：{np.sum(outliers)}")

---

DBSCAN（基于密度的聚类）

原理

DBSCAN 是一种基于密度的聚类算法，也可用于异常检测。核心概念：

• 密度高 → 属于簇
• 密度低 → 被视为噪声（异常）

DBSCAN 通过两个参数：

• eps：半径
• min_samples：最小邻居数

若一个点邻域内不足 min_samples，则判定为噪声，即异常。

方法流程

1. 选择 eps 和 min_samples
2. 定义核心点
3. 聚合簇
4. 将噪声点标记为异常

优点

• 不需预设簇数
• 能识别任意形状的簇
• 异常检测与聚类天然结合

缺点

• 对 eps 参数敏感
• 高维空间密度难以定义
• 大数据时计算量较高

应用场景

• 空间地理数据聚类
• 图像区域检测
• 小规模数据异常检测

重要参数

参数名	含义	是否影响检测结果	建议
eps	邻域半径，越小则聚类更紧凑	高	需调参，可用 k-distance plot
min_samples	邻域内最少样本数	高	通常设 3~10
metric	距离度量方式（如 euclidean, manhattan）	中	一般用默认 euclidean

• eps 是 DBSCAN 中最敏感的参数

Python 示例

import numpy as np
from sklearn.cluster import DBSCAN
from sklearn.neighbors import NearestNeighbors

# 生成数据
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])
data = data.reshape(-1, 1)

# 估算 eps
neighbors = NearestNeighbors(n_neighbors=5)
neighbors_fit = neighbors.fit(data)
distances, _ = neighbors_fit.kneighbors(data)
k_distances = np.sort(distances[:, -1])
eps = np.percentile(k_distances, 90)

# DBSCAN
model = DBSCAN(eps=eps, min_samples=5)
labels = model.fit_predict(data)

outliers = labels == -1

print(f"异常值数量：{np.sum(outliers)}")

---

LOF（Local Outlier Factor）

原理

LOF 基于局部密度：

• 若某样本的密度远低于邻居平均密度，则判定为异常

能检测局部异常，不依赖全局分布。

方法流程

1. 找到每个样本的 k 邻居
2. 计算局部可达密度
3. 计算 LOF = 邻域平均密度 / 自身密度
4. LOF > 1 即为异常

优点

• 能发现局部异常
• 不依赖分布假设
• 适合复杂数据分布

缺点

• 对 k 敏感
• 高维数据较慢
• 不适合极高维场景

应用场景

• 信用卡欺诈检测
• 工业局部波动检测
• 空间分析

重要参数

参数名	含义	是否影响检测结果	建议
n_neighbors	k 值，影响局部密度计算	高	建议 10~30
contamination	异常比例	高	根据实际比例设定
metric	距离度量（euclidean, manhattan 等）	中	通常用默认

• n_neighbors 是关键参数，影响检测灵敏度

Python 示例

import numpy as np
from sklearn.neighbors import LocalOutlierFactor

# 生成数据
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])
data = data.reshape(-1, 1)

# LOF
model = LocalOutlierFactor(n_neighbors=20, contamination=0.05)
scores = model.fit_predict(data)
outliers = scores == -1

print(f"异常值数量：{np.sum(outliers)}")

---

KDE（Kernel Density Estimation）

原理

KDE 是基于概率密度估计：

• 用核函数平滑每个观测值
• 密度最低的区域即为异常

常用于单变量或低维数据。

方法流程

1. 对每个样本建立核函数
2. 所有核函数求和，生成密度曲线
3. 低密度区域即异常

优点

• 适合复杂分布
• 不需分布假设
• 灵活调整核函数

缺点

• 高维数据效果差
• 带宽选择困难
• 计算较慢

应用场景

• 金融分布分析
• 单变量异常检测
• 图像灰度分布分析

重要参数

参数名	含义	是否影响检测结果	建议
bandwidth	平滑程度，越大越平滑	高	可网格搜索
kernel	核类型（gaussian, tophat 等）	中	一般用 gaussian

• bandwidth 是最敏感参数

Python 示例

import numpy as np
from sklearn.neighbors import KernelDensity

# 生成数据
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])
data = data.reshape(-1, 1)

# KDE
kde = KernelDensity(bandwidth=0.5)
kde.fit(data)
log_density = kde.score_samples(data)
density = np.exp(log_density)

# 阈值取密度最低 5%
threshold = np.percentile(density, 5)
outliers = density < threshold

print(f"异常值数量：{np.sum(outliers)}")

也可以通过调整参数

场景	推荐 bandwidth 范围
数据集中、尖锐峰值	小（0.1 ~ 0.5）
数据较平滑、单峰	中（0.5 ~ 1.0）
数据很分散、粗略趋势观察	大（1.0 ~ 2.0）

import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KernelDensity
import matplotlib.pyplot as plt

# 数据
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])
data = data.reshape(-1, 1)

# Grid Search
params = {'bandwidth': np.linspace(0.1, 2.0, 20)}
grid = GridSearchCV(KernelDensity(), params, cv=3)
grid.fit(data)

print("最佳 bandwidth：", grid.best_estimator_.bandwidth)

# 用最佳 bandwidth
kde = KernelDensity(bandwidth=grid.best_estimator_.bandwidth)
kde.fit(data)

# 计算密度
log_density = kde.score_samples(data)
density = np.exp(log_density)

# 阈值
threshold = np.percentile(density, 5)
outliers = density < threshold

print(f"检测到异常值数量：{np.sum(outliers)}")

# 可视化
plt.scatter(range(len(data)), data, c=outliers, cmap='coolwarm')
plt.title("KDE 异常检测 (红色为异常)")
plt.show()

---

COPOD

原理

COPOD 基于 Copula 理论：

• 将数据转为边缘累积分布
• 建立 Copula 模型
• tail probability 判定异常

完全无参，适合多维数据。

方法流程

1. 转换边缘累积分布
2. 建 Copula 模型
3. 计算 tail probability
4. 判定异常

优点

• 无需超参数
• 不依赖分布假设
• 高维友好

缺点

• 小样本场景不稳定
• 对高度线性数据可能过拟合

应用场景

• 金融风控
• 异常交易检测
• 网络流量监控

重要参数

• 无主要超参数。COPOD 完全是无参数算法。

唯一可能设置的：

参数名	含义	是否影响检测结果	建议
contamination	异常比例	高	根据实际数据设

• contamination 决定最终判定阈值

Python 示例

import numpy as np
from pyod.models.copod import COPOD

# 生成数据
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])
data = data.reshape(-1, 1)

# COPOD
model = COPOD(contamination=0.05)
model.fit(data)
outliers = model.predict(data) == 1

print(f"异常值数量：{np.sum(outliers)}")

---

ECOD

原理

ECOD 基于经验累积分布：

• 无模型拟合
• 利用 ECDF 判断尾部数据为异常

方法流程

1. 计算 ECDF
2. Tail probability 越小，越异常

优点

• 极快
• 无参数
• 非常简单易解释

缺点

• 高维表现有限
• 无法捕捉变量间相关性

应用场景

• 小数据异常检测
• 监控指标
• 自动质控

重要参数

参数名	含义	是否影响检测结果	建议
contamination	异常比例	高	建议与实际数据相符

• contamination 是关键，决定阈值。

Python 示例

import numpy as np
from pyod.models.ecod import ECOD

# 生成数据
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])
data = data.reshape(-1, 1)

# ECOD
model = ECOD(contamination=0.05)
model.fit(data)
outliers = model.predict(data) == 1

print(f"异常值数量：{np.sum(outliers)}")

---

HBOS（Histogram-Based Outlier Score）

原理

HBOS 是直方图方法：

• 对每维数据建立直方图
• 落在低频 bin 的样本被视为异常

假设特征独立，通过概率密度乘积检测异常。

方法流程

1. 为每维度建直方图
2. 计算各观测值的概率密度
3. 概率乘积
4. 概率越低 → 越异常

优点

• 非常快
• 实现简单
• 不需复杂模型

缺点

• 假设各维度独立
• 高维效果有限
• 默认参数会影响检测比例

重要参数

参数名	含义	是否影响检测结果	建议
n_bins	分箱数，影响直方图细度	高	10~50 之间调整
alpha	平滑参数，避免概率为零	中	0.01~0.1
contamination	异常比例，决定阈值	高	根据实际异常比例设置

• contamination 是最重要的，决定多少数据被判异常

Python 示例

import numpy as np
from pyod.models.hbos import HBOS

# 生成数据
data = np.concatenate([np.random.normal(0, 1, 950), np.random.uniform(8, 12, 50)])
data = data.reshape(-1, 1)

# HBOS
model = HBOS(contamination=0.05)
model.fit(data)
outliers = model.predict(data) == 1

print(f"异常值数量：{np.sum(outliers)}")

---

方法	是否无监督	高维支持	自动阈值	异常检测特色
IQR	否	差	否	统计学基础，简单快速
Isolation Forest	是	强	是	随机分割思想，高效处理高维数据
DBSCAN	是	差	是	密度聚类，自然识别噪声
LOF	是	中	否	局部密度检测，捕捉局部异常
KDE	是	差	否	基于概率密度，适合一维/低维数据
COPOD	是	强	是	Copula 理论，无需参数，高维友好
ECOD	是	中	是	基于经验分布，无需参数，速度快
HBOS	是	中	是	直方图方式，极快速度，适合大数据

综合代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest
from sklearn.cluster import DBSCAN
from sklearn.neighbors import LocalOutlierFactor
from sklearn.svm import OneClassSVM
from sklearn.neighbors import KernelDensity
from pyod.models.copod import COPOD
from pyod.models.ecod import ECOD
from pyod.models.hbos import HBOS
from scipy import stats

# 1. 生成示例数据 - 1000个数值点（包含5%异常值）
np.random.seed(42)
normal_data = np.random.normal(0, 1, 950)  # 95%正常数据
outliers = np.random.uniform(8, 12, 50)  # 5%异常值
data = np.concatenate([normal_data, outliers])
np.random.shuffle(data)  # 打乱数据顺序

print(f"数据集大小: {len(data)}")
print(f"数据范围: {min(data):.2f} 到 {max(data):.2f}")

# 2. 可视化原始数据
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.hist(data, bins=50, alpha=0.7)
plt.title('数据分布直方图')
plt.xlabel('数值')
plt.ylabel('频次')

plt.subplot(2, 1, 2)
plt.boxplot(data, vert=False)
plt.title('箱线图')
plt.tight_layout()
plt.show()


# 3. 异常检测方法实现
# 注意：所有方法都使用默认参数或自动模式，无需手动设置阈值

def detect_outliers_iqr(data):
    """
    IQR方法 (需要设置倍数，但通常使用1.5作为默认值)
    优点：简单快速，对非正态分布有效
    """
    q1, q3 = np.percentile(data, [25, 75])
    iqr = q3 - q1
    lower_bound = q1 - 1.5 * iqr
    upper_bound = q3 + 1.5 * iqr
    return (data < lower_bound) | (data > upper_bound)


def detect_outliers_isolation_forest(data):
    """
    隔离森林 (使用自动异常比例检测)
    优点：无需数据分布假设，自动检测异常
    """
    model = IsolationForest(contamination="auto", random_state=42)
    # 转为2D数组 (1000, 1)
    return model.fit_predict(data.reshape(-1, 1)) == -1


def detect_outliers_dbscan(data):
    """
    DBSCAN聚类方法 (自动将噪声点识别为异常)
    优点：完全无监督，无需指定异常比例
    注意：需要调整eps和min_samples参数，但这里使用自动估算
    """
    # 自动估算eps - 使用k距离图的中位数
    from sklearn.neighbors import NearestNeighbors
    neighbors = NearestNeighbors(n_neighbors=5)
    neighbors_fit = neighbors.fit(data.reshape(-1, 1))
    distances, _ = neighbors_fit.kneighbors(data.reshape(-1, 1))
    k_distances = np.sort(distances[:, -1])
    eps = np.percentile(k_distances, 90)  # 取90%分位数作为eps

    model = DBSCAN(eps=eps, min_samples=5)
    clusters = model.fit_predict(data.reshape(-1, 1))
    return clusters == -1  # 噪声点即异常值


def detect_outliers_lof(data):
    """
    局部异常因子 (LOF) - 通过得分自动识别异常
    优点：检测局部异常，不依赖全局分布
    """
    model = LocalOutlierFactor(n_neighbors=20, contamination="auto")
    model.fit(data.reshape(-1, 1))
    # 负值越大越正常，负值越小越异常
    scores = model.negative_outlier_factor_
    # 自动阈值：低于平均值2个标准差
    threshold = np.mean(scores) - 2 * np.std(scores)
    return scores < threshold


def detect_outliers_kde(data):
    """
    核密度估计 (KDE) - 通过概率密度自动识别异常
    优点：基于概率模型，适合复杂分布
    """
    # 自动选择带宽参数
    kde = KernelDensity(bandwidth=0.5)
    kde.fit(data.reshape(-1, 1))
    log_density = kde.score_samples(data.reshape(-1, 1))
    density = np.exp(log_density)
    # 自动阈值：密度最低的5%
    threshold = np.percentile(density, 5)
    return density < threshold


def detect_outliers_copod(data):
    """
    COPOD方法 (完全无参数)
    优点：基于Copula理论，无需任何参数设置
    """
    model = COPOD()
    model.fit(data.reshape(-1, 1))
    # COPOD自动计算阈值
    return model.predict(data.reshape(-1, 1)) == 1


def detect_outliers_ecod(data):
    """
    ECOD方法 (完全无参数)
    优点：基于经验累积分布，无需参数
    """
    model = ECOD()
    model.fit(data.reshape(-1, 1))
    # ECOD自动计算阈值
    return model.predict(data.reshape(-1, 1)) == 1


def detect_outliers_hbos(data):
    """
    HBOS方法 (直方图基础，几乎无参数)
    优点：极快，适合大数据
    """
    model = HBOS()
    model.fit(data.reshape(-1, 1))
    # HBOS自动计算阈值
    return model.predict(data.reshape(-1, 1)) == 1


# 4. 执行所有检测方法
methods = {
    "IQR": detect_outliers_iqr,
    "Isolation Forest": detect_outliers_isolation_forest,
    "DBSCAN": detect_outliers_dbscan,
    "LOF": detect_outliers_lof,
    "KDE": detect_outliers_kde,
    "COPOD": detect_outliers_copod,
    "ECOD": detect_outliers_ecod,
    "HBOS": detect_outliers_hbos
}

results = {}
for name, method in methods.items():
    results[name] = method(data)
    print(f"{name} 检测到异常值数量: {sum(results[name])}")

# 5. 可视化比较结果
plt.figure(figsize=(15, 10))

# 原始数据位置图
plt.subplot(3, 1, 1)
plt.scatter(range(len(data)), data, alpha=0.6)
plt.title('原始数据分布')
plt.xlabel('索引')
plt.ylabel('数值')

# 异常值检测结果比较
plt.subplot(3, 1, 2)
colors = plt.cm.tab10.colors
for i, (name, outliers) in enumerate(results.items()):
    outlier_indices = np.where(outliers)[0]
    plt.scatter(outlier_indices, [i] * len(outlier_indices),
                color=colors[i % 10], label=name, alpha=0.7)

plt.yticks(range(len(methods)), list(methods.keys()))
plt.title('不同方法检测到的异常点位置')
plt.xlabel('数据索引')
plt.legend()

# 异常值在数值轴上的分布
plt.subplot(3, 1, 3)
for i, (name, outliers) in enumerate(results.items()):
    outlier_values = data[outliers]
    plt.scatter(outlier_values, [i] * len(outlier_values),
                color=colors[i % 10], alpha=0.7)

plt.yticks(range(len(methods)), list(methods.keys()))
plt.title('异常点的数值分布')
plt.xlabel('数值')
plt.tight_layout()
plt.show()

# 6. 输出统计摘要
print("\n异常检测结果统计:")
print("-" * 50)
print(f"{'方法':<20} | {'异常值数量':<10} | {'异常值比例':<10}")
print("-" * 50)
for name, outliers in results.items():
    count = sum(outliers)
    ratio = count / len(data)
    print(f"{name:<20} | {count:<10} | {ratio:.2%}")

其他

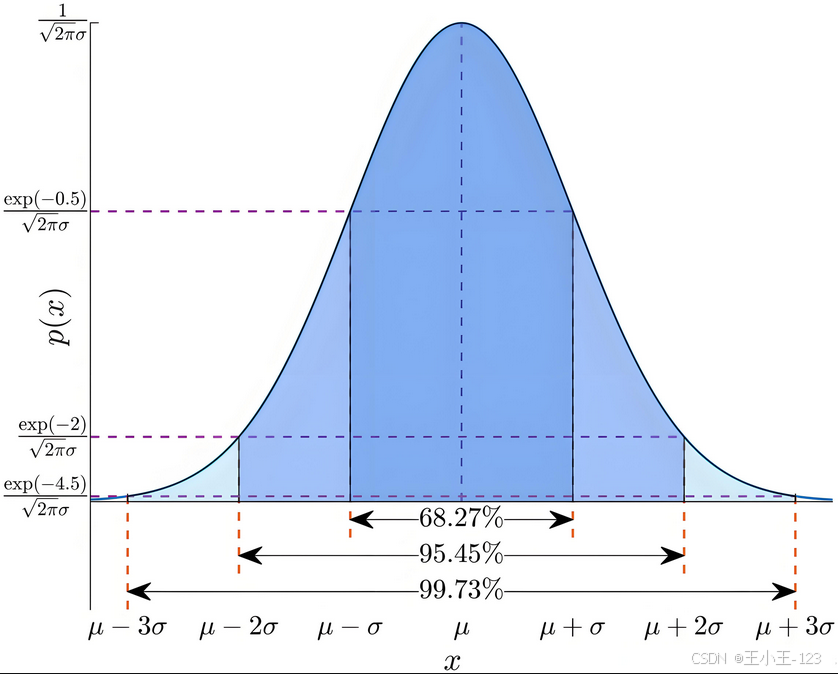
假设数据样本是符合正态分布的，通过计算出每一个数据样本的概率密度值，这个值直接的反映出了它的集中程度，如果分布在尾部两端，这个值会比较小，这个时候需要一个阈值来判断，为了避免每次人为主观设定，采用1/样本数进行权衡。

from scipy.stats import norm
import numpy as np
# 假设你的数据
data = np.array([32, 35, 31, 38, 30, 32, 10.1])
# 计算样本均值和标准差
mu = np.mean(data)
sigma = np.std(data, ddof=1)
# 计算每个点的概率密度值
pdf_values = norm.pdf(data, loc=mu, scale=sigma)
print("每个点的概率密度值:", pdf_values)
print(1/len(pdf_values))

正态分布检测

import numpy as np
from scipy import stats

def objective_normality_test(data, alpha=0.05):
    """
    完全客观量化检验1000个样本点是否符合正态分布
    
    参数:
    data -- 包含1000个样本点的数组或列表
    alpha -- 显著性水平 (默认0.05)
    
    返回:
    包含所有量化指标的字典
    """
    n = len(data)
    if n != 1000:
        print(f"警告: 样本量={n}, 建议使用1000个样本点")
    
    # 1. 基本描述统计量
    mean = np.mean(data)
    std = np.std(data, ddof=1)  # 样本标准差
    
    # 2. 正态性检验
    # Shapiro-Wilk检验 (样本量≤5000有效)
    shapiro_stat, shapiro_p = stats.shapiro(data)
    
    # D'Agostino's K²检验 (基于偏度和峰度)
    dagostino_stat, dagostino_p = stats.normaltest(data)
    
    # Anderson-Darling检验 (严格检验)
    anderson_result = stats.anderson(data, dist='norm')
    ad_stat = anderson_result.statistic
    ad_critical = anderson_result.critical_values[2]  # α=0.05的临界值
    
    # 3. 偏度和峰度
    skewness = stats.skew(data)
    kurtosis = stats.kurtosis(data)  # 超额峰度
    
    # 4. 量化评分系统 (满分100分)
    score = 0
    
    # Shapiro-Wilk检验 (25分)
    if shapiro_p >= alpha:
        score += 25
    elif shapiro_p >= alpha/2:  # 部分分数
        score += 10
    
    # D'Agostino's K²检验 (25分)
    if dagostino_p >= alpha:
        score += 25
    elif dagostino_p >= alpha/2:
        score += 10
    
    # Anderson-Darling检验 (20分)
    if ad_stat < ad_critical:
        score += 20
    elif ad_stat < ad_critical * 1.1:  # 轻微偏离
        score += 10
    
    # 偏度 (15分)
    abs_skew = abs(skewness)
    if abs_skew < 0.3:
        score += 15
    elif abs_skew < 0.5:
        score += 10
    elif abs_skew < 1.0:
        score += 5
    
    # 峰度 (15分)
    abs_kurt = abs(kurtosis)
    if abs_kurt < 0.3:
        score += 15
    elif abs_kurt < 0.5:
        score += 10
    elif abs_kurt < 1.0:
        score += 5
    
    # 5. 最终结论
    if score >= 90:
        conclusion = "高度符合正态分布"
    elif score >= 75:
        conclusion = "基本符合正态分布"
    elif score >= 60:
        conclusion = "勉强符合正态分布（轻微偏离）"
    else:
        conclusion = "不符合正态分布"
    
    # 返回所有量化指标
    return {
        "样本量": n,
        "均值": mean,
        "标准差": std,
        "Shapiro-Wilk检验": {
            "统计量": shapiro_stat,
            "p值": shapiro_p,
            "结果": "通过" if shapiro_p >= alpha else "未通过"
        },
        "D'Agostino's K²检验": {
            "统计量": dagostino_stat,
            "p值": dagostino_p,
            "结果": "通过" if dagostino_p >= alpha else "未通过"
        },
        "Anderson-Darling检验": {
            "统计量": ad_stat,
            "临界值(α=0.05)": ad_critical,
            "结果": "通过" if ad_stat < ad_critical else "未通过"
        },
        "偏度": {
            "值": skewness,
            "绝对值": abs_skew,
            "评估": "正常" if abs_skew < 0.5 else "偏高"
        },
        "峰度": {
            "值": kurtosis,
            "绝对值": abs_kurt,
            "评估": "正常" if abs_kurt < 0.5 else "偏高"
        },
        "综合评分": score,
        "结论": conclusion
    }

# 示例使用
if __name__ == "__main__":
    # 生成测试数据（1000个样本点）
    np.random.seed(42)  # 确保可重复性
    
    # 正态分布数据
    normal_data = np.random.normal(loc=0, scale=1, size=1000)
    
    # 非正态分布数据（指数分布）
    non_normal_data = np.random.exponential(scale=1, size=1000)
    
    print("正态数据检验结果:")
    normal_result = objective_normality_test(normal_data)
    for key, value in normal_result.items():
        if isinstance(value, dict):
            print(f"\n{key}:")
            for subkey, subval in value.items():
                print(f"  {subkey}: {subval}")
        else:
            print(f"{key}: {value}")
    
    print("\n" + "="*50 + "\n")
    
    print("非正态数据检验结果:")
    non_normal_result = objective_normality_test(non_normal_data)
    for key, value in non_normal_result.items():
        if isinstance(value, dict):
            print(f"\n{key}:")
            for subkey, subval in value.items():
                print(f"  {subkey}: {subval}")
        else:
            print(f"{key}: {value}")

每文一语

有事多赚钱，没事早睡觉