(数据结构)如何手搓一棵红黑树(RedBlack-Tree)
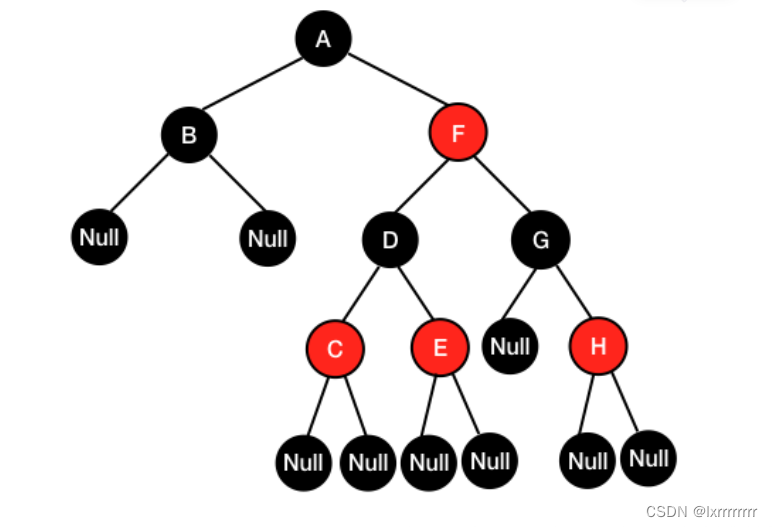
红黑树作为一种及其高级的数据结构,插入和删除效率很高,被广泛用于各种底层设计上与B树有着不解之缘其中一颗红黑树必须满足这样的性质1 根节点是黑色2 每个叶子节点(就是最末端的节点也就是null)是黑色(一般画图省略null)3 如果一个节点是红色,那么它的两个子节点都是黑色(也就是说不能有两个相邻的红色节点)4 从任一 节点开始到其所有子孙叶结点的路径中所包含的黑色结点数量必须相同。
目录
红黑树作为一种及其高级的数据结构,插入和删除效率很高,被广泛用于各种底层设计上
与B树有着不解之缘
其中一颗红黑树必须满足这样的性质
1 根节点是黑色
2 每个叶子节点(就是最末端的节点也就是null)是黑色(一般画图省略null)
3 如果一个节点是红色,那么它的两个子节点都是黑色(也就是说不能有两个相邻的红色节点)
4 从任一 节点开始到其所有子孙叶结点的路径中所包含的黑色结点数量必须相同。
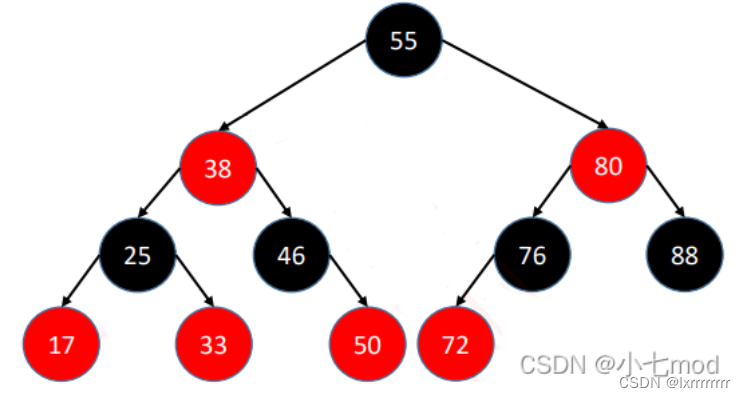
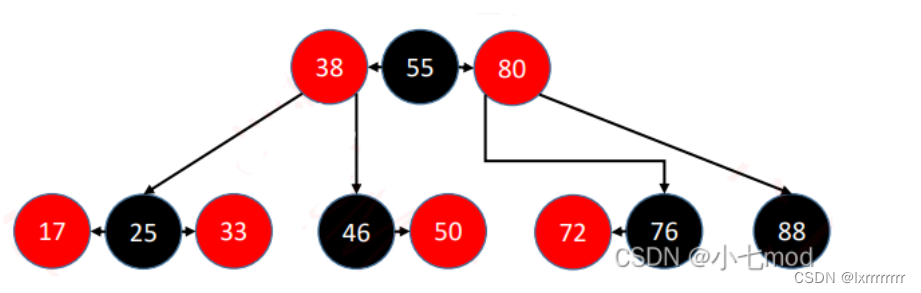
看似`红黑树`具有更加奇怪的平衡条件,实际上`红黑树`与`B树`具有非常紧密的联系——将红黑树的红色节点向上依附于黑色节点,就构成了一棵`2-4 B树`,(如下图)因此`红黑树`的黑高度即等于与之对应的B树的高度,这样一来红黑树的平衡性就不证自明了。对于红黑树的失衡调整算法的理解,关键也在于将它转化为等效的B树,通过B树的上溢和下溢调整算法来理解。
函数总览
#define ISBLACK(x) (!x || x->color == BLACK)
#define ISRED(x) (x && x->color == RED)
#define BLACK_HEIGHT(x) (x? x->height:0)
#define BLACK_HEIGHT_CHANGED(x) (x&&BLACK_HEIGHT(x->leftchild)!=BLACK_HEIGHT(x->rightchild))
#define T entry<K,V>
template <typename K,typename V>
class lxrRedBlack:public lxrBST<K,V>{
protected:
lxrbinnodeposi(T) zig(lxrbinnodeposi(T) p); //right rotation
lxrbinnodeposi(T) zag(lxrbinnodeposi(T) p); //left rotation
void solveDoubleRed(lxrbinnodeposi(T) x);
void solveDoubleBlack(lxrbinnodeposi(T) x);
bool updateHeight(lxrbinnodeposi(T) x);
public:
lxrbinnodeposi(T) insert(K const &key,V const &value);
bool remove(K const &key);
};
//protected methods旋转函数
在解决后面双黑缺陷时,我们要进行旋转操作,和上次一样,提前写好两个单层旋转函数
template <typename K,typename V>
lxrbinnodeposi(T) lxrRedBlack<K,V>::zig(lxrbinnodeposi(T) p){
lxrbinnodeposi(T) x=p->leftchild;
p->leftchild=x->rightchild;
if(x->rightchild) x->rightchild->parent=p;
x->rightchild=p;
p->parent=x;
return x;
}
template <typename K,typename V>
lxrbinnodeposi(T) lxrRedBlack<K,V>::zag(lxrbinnodeposi(T) p){
lxrbinnodeposi(T) x=p->rightchild;
p->rightchild=x->leftchild;
if(x->leftchild) x->leftchild->parent=p;
x->leftchild=p;
p->parent=x;
return x;
}更新高度
此外,对于一颗红黑树,我们要重写update函数,来更新每个节点的黑高度
template <typename K,typename V>
bool lxrRedBlack<K,V>::updateHeight(lxrbinnodeposi(T) x){
if(!x) return false;
int prevHeight=BLACK_HEIGHT(x);
if(ISBLACK(x->leftchild))
x->height=BLACK_HEIGHT(x->leftchild)+1;
else x->height=BLACK_HEIGHT(x->leftchild);
return prevHeight!=x->height;
}
双红缺陷
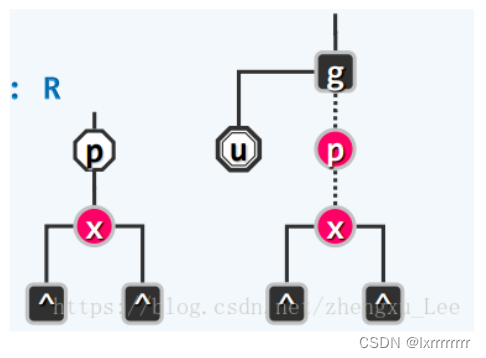
我们在插入时,会将新插入节点染红,如果他的父节点也是红,那就导致了双红缺陷
对于插入操作,可能会出现`双红缺陷`(double red),此时需要对被插入节点的叔父节点进行讨论,如果叔父为黑色节点,则做一次`3+4重构`即可,等效于`B树`中交换相邻的红黑节点的颜色;
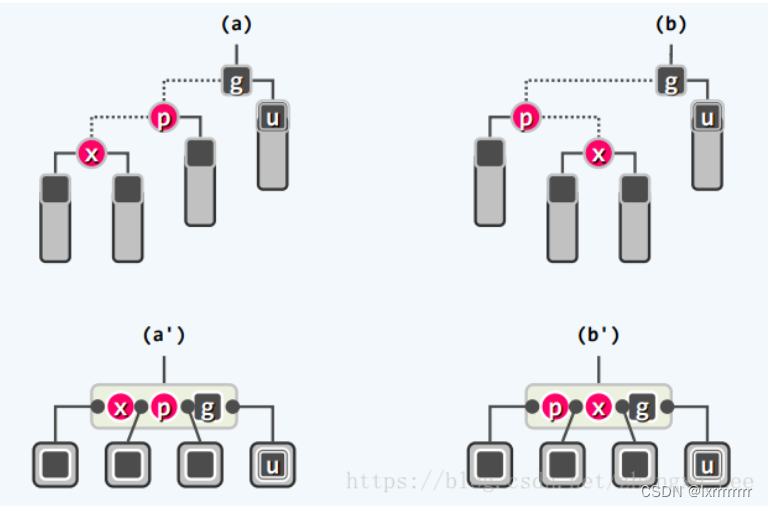
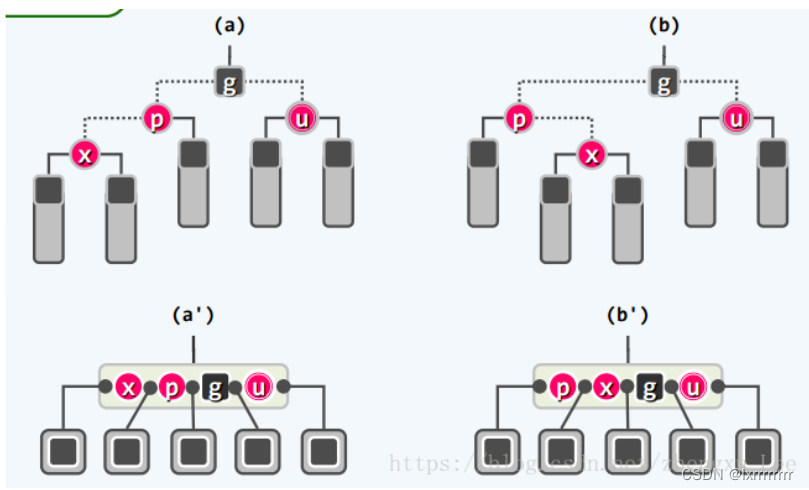
如果叔父的红色节点,则对应于`B树`中的`上溢`,此时只需要将祖父染成黑色,而将父节点和叔父节点都染成红色,即可在这一局部解决`双红缺陷`,但需要注意的是,`双红缺陷`可能在祖父节点再次出现。这对应了`B树`中解决`上溢`的`split`操作,分裂节点后可能导致上一层节点继续`上溢`。
template <typename K,typename V>
void lxrRedBlack<K,V>::solveDoubleRed(lxrbinnodeposi(T) x){
lxrbinnodeposi(T) p=x->parent;
if(!p) {x->color=BLACK;return; } //x is root
if(ISBLACK(p)) return ;
//double red
lxrbinnodeposi(T) g=p->parent; //assert g exists
lxrbinnodeposi(T) s=(p==g->leftchild ? g->rightchild : g->leftchild); //s is uncle of x
if(ISBLACK(s)){// s is black
lxrbinnodeposi(T) gg =g->parent;
lxrbinnodeposi(T) newRoot=this->rotateAt(x);
if(gg)
(g==gg->leftchild ? gg->leftchild : gg->rightchild)=newRoot;
else this->__root=newRoot;
newRoot->color=BLACK;
newRoot->leftchild->color=RED;
newRoot->rightchild->color=RED;
updateHeight(newRoot->leftchild);
updateHeight(newRoot->rightchild);
updateHeight(newRoot);
return ;
}
else{// s is red
g->color=RED;
s->color=BLACK;
p->color=BLACK;
updateHeight(g);
solveDoubleRed(g);
}
}
双黑缺陷
对于删除操作,可能会出现`双黑缺陷`(double black),对应了`B树`中的`下溢`。为了解决`下溢`,首先需要`左顾右盼`,因此首先要找到下溢节点的邻居节点,记为`s`。当下溢节点的兄弟节点为黑色时,`s`即为该兄弟节点,如果`s`有红色的孩子,意味着从`s`借一个孩子即可解决`双黑缺陷`,对应了红黑树中对`s`的红色孩子进行一次`3+4重构`;如果`s`全是黑色的孩子,则无节点可借,为此只能进行节点的合并。如果父节点`p`为红色,则意味着上层超级节点有多余的节点可供合并,合并后并不会引起更高层的`下溢`,这对应了红黑树中将`p`和`s`交换颜色;如果父节点`p`为黑色,意味着上一层的超级节点刚好在`下溢`的边缘,合并后必然引起`下溢`向高层传递,这对应了红黑树中将`s`染红,然后`双黑缺陷`向上传递两层,即假想地认为刚刚删除了`p`的黑色父亲。
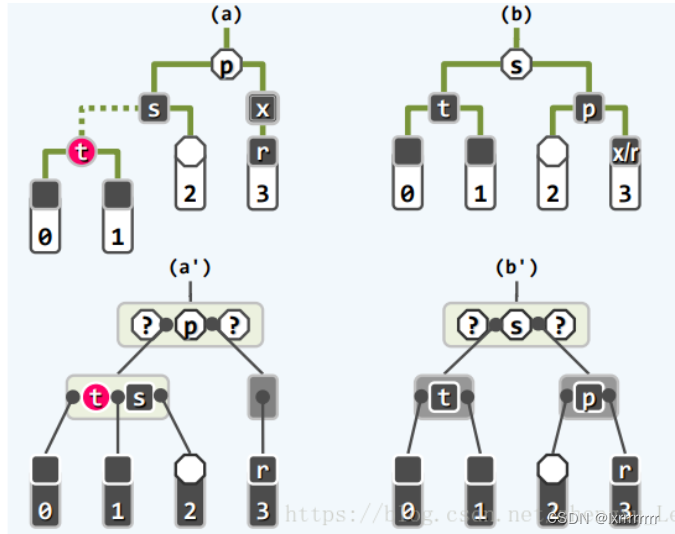
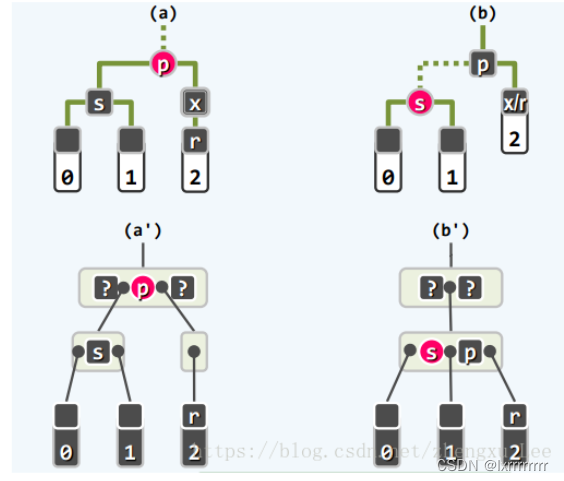
上面的讨论都是基于`s`就是被删除节点的兄弟节点,而如果`x`的兄弟节点是红色,`s`应该是`x`的兄弟节点的孩子节点,此后还需要对该孩子节点进行类似于上面的讨论,未免过于复杂。为了对问题进行简化,不妨简单地将`s`和`p`进行一次单旋转,并且交换它们的颜色,这对应了`B树`中将超级节点中的`s`和`p`交换颜色,此时虽然并没有解决`双黑缺陷`,可是这样交换以后,`s`必为黑色节点了,并且`p`是红色节点,因此问题就转化成了上面讨论过的第一种或者第二种情况。
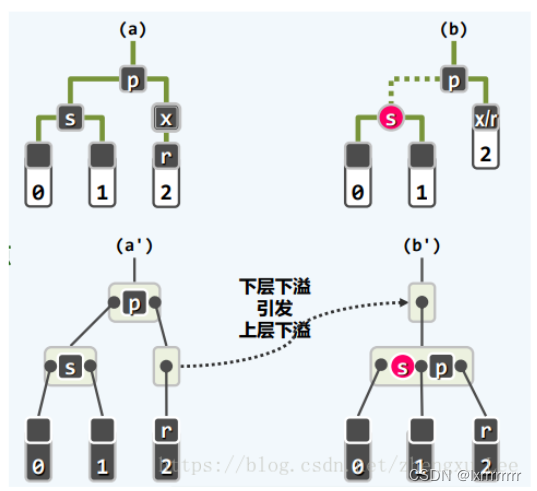
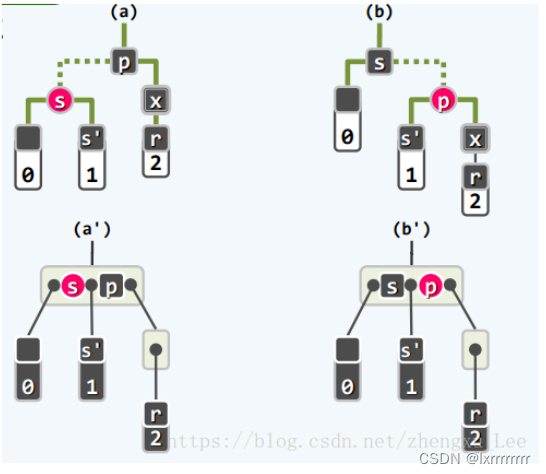
template<typename K,typename V>
void lxrRedBlack<K,V>::solveDoubleBlack(lxrbinnodeposi(T) x){
if(x==this->__root) return ;
lxrbinnodeposi(T) p=(x ? x->parent : this->__hot);
lxrbinnodeposi(T) s=(x==p->leftchild ? p->rightchild : p->leftchild);
//s has at least one red child
if(ISRED(s->leftchild) || ISRED(s->rightchild)){
lxrbinnodeposi(T) redChild=ISRED(s->leftchild) ? s->leftchild : s->rightchild;
lxrbinnodeposi(T) g=p->parent;
lxrbinnodeposi(T) newRoot=this->rotateAt(redChild);
if(g)
(p==g->leftchild ? g->leftchild : g->rightchild)=newRoot;
else this->__root=newRoot;
redChild->color=BLACK;
updateHeight(newRoot->leftchild);
updateHeight(newRoot->rightchild);
updateHeight(newRoot);
return ;
}
// p is red
if(ISRED(p)){
p->color=BLACK;
s->color=RED;
updateHeight(p);
return ;
}
//p is black and s is black
if(ISBLACK(p) && ISBLACK(s)){
p->color=BLACK;
s->color=RED;
updateHeight(p);
solveDoubleBlack(p);
return ;
}
//s is red
if(ISRED(s)){
p->color=RED;
s->color=BLACK;
lxrbinnodeposi(T) g=p->parent;
if(s==p->leftchild) zig(p);
else zag(p);
s->parent=g;
if(g) (p==g->leftchild ? g->leftchild : g->rightchild)=s;
else this->__root=s;
solveDoubleBlack(x);
}
}容易看到,对于红黑树的失衡调整算法,一旦进行了一次结构调整,全树必然恢复平衡,因此红黑树的每次的结构调整量仅为O(1),而AVL树只有插入的调整才能做到这点,其删除算法至多会进行O(logn)次结构调整。
insert
对于插入操作,由于我们插入的每个节点初始都为红色,易导致双红缺陷
所以在插入后面还要加上相应的处理函数
template <typename K,typename V>
lxrbinnodeposi(T) lxrRedBlack<K,V>::insert(K const &key,V const &value){
lxrbinnodeposi(T) &x=this->search(key);
if (x) return x;
x=new lxrbinnode<T>(entry<K,V>(key,value),this->__hot,RED);
x->height=1;
++(this->__size);
solveDoubleRed(x);
return x;
}remove
同样的,对于删除操作,易导致双黑缺陷,用上述方法处理即可
template <typename K,typename V>
bool lxrRedBlack<K,V>::remove(K const &key){
lxrbinnodeposi(T) &x=this->search(key);
if(!x) return false;
lxrbinnodeposi(T) succ=this->removeAt(x,this->__hot);
--(this->__size);
if(ISRED(succ)){
succ->color=BLACK;
return true;
}
if(!BLACK_HEIGHT_CHANGED(this->__hot)) return true;
solveDoubleBlack(succ);
return true;
}
魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容







所有评论(0)