数据结构(四)——串的模式匹配
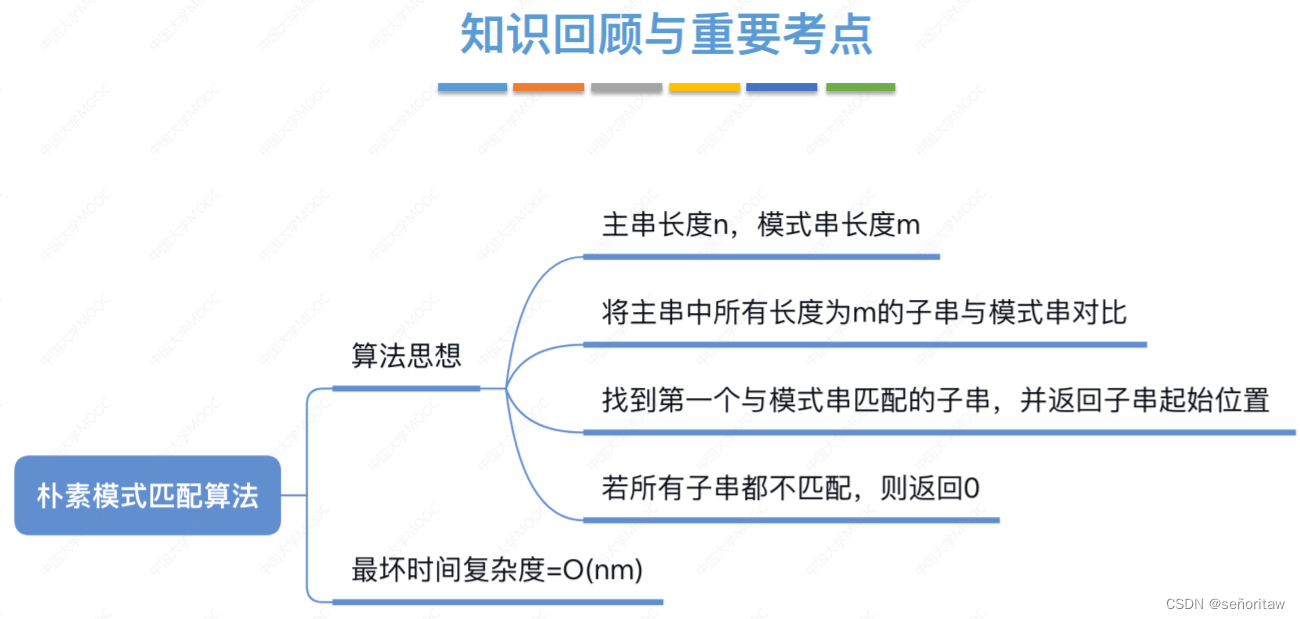
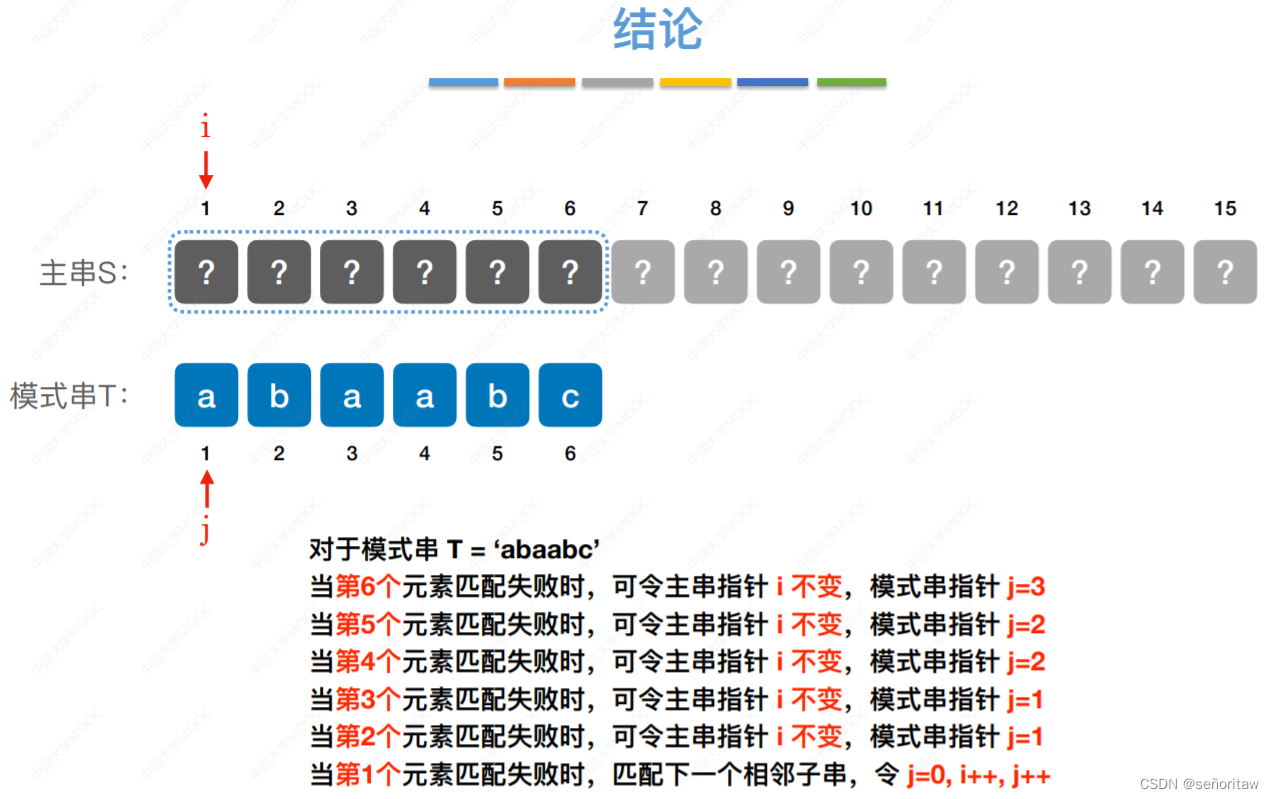
主串⻓度为n,模式串⻓度为 m 朴素模式匹配算法:将主串中所有⻓度为m的⼦串依次与模式串对⽐,直到找到⼀个完全匹配的⼦串, 或所有的⼦串都不匹配为⽌。接下来的字符,在不匹配的位置前划一根分界线,模式串一步一步往后退,直到分界线前的“对的上”,或模式串完全越过分界线位置,如下面为第3个字符不匹配的情况。最坏的情况,每个⼦串都要对⽐ m 个字符,共 n-m+1 个⼦串,复杂度 = O((n-m+1)m
4.2 串的模式匹配
4.2.1_朴素模式匹配算法
字符串模式匹配:在主串中找到与模式串相同的⼦串,并返回其所在位置
主串⻓度为n,模式串⻓度为 m 朴素模式匹配算法:将主串中所有⻓度为m的⼦串依次与模式串对⽐,直到找到⼀个完全匹配的⼦串, 或所有的⼦串都不匹配为⽌。 最多对⽐ n-m+1 个⼦串
Index(S,T):定位操作。若主串S中存在与串T值相同的⼦串,则返回它在主串S中第⼀次出现 的位置;否则函数值为0
接下来不使用字符串的基本操作,直接通过数组下标实现朴素模式匹配算法
// 在主串S中找到与模式串T相同的子串并返回其位序,否则返回0
int Index(SString S, SString T){
int i=1, j=1;
while(i<=S.length && j<=T.length){
if(S.ch[i] == T.ch[j]){ //如果i里面存的字符和j里面存的相同的话
++i; ++j; //++继续比较后继字符
}else{
i=i-j+2; //i指针指向下一个子串的起始位置
j=1; //j指针后退回到第一个位置重新开始匹配
}
}
if(j>T.length)
return i-T.length;
else
return 0;
}
设主串⻓度为 n,模式串⻓度为 m,则 最坏时间复杂度 = O(nm)
最坏的情况,每个⼦串都要对⽐ m 个字符,共 n-m+1 个⼦串,复杂度 = O((n-m+1)m) = O(nm)
4.2.2_1_KMP算法
朴素模式匹配算法的缺点
⼀旦发现当前这个⼦串中某个字符不匹配,就只能转⽽匹配下⼀个⼦串(从头开始)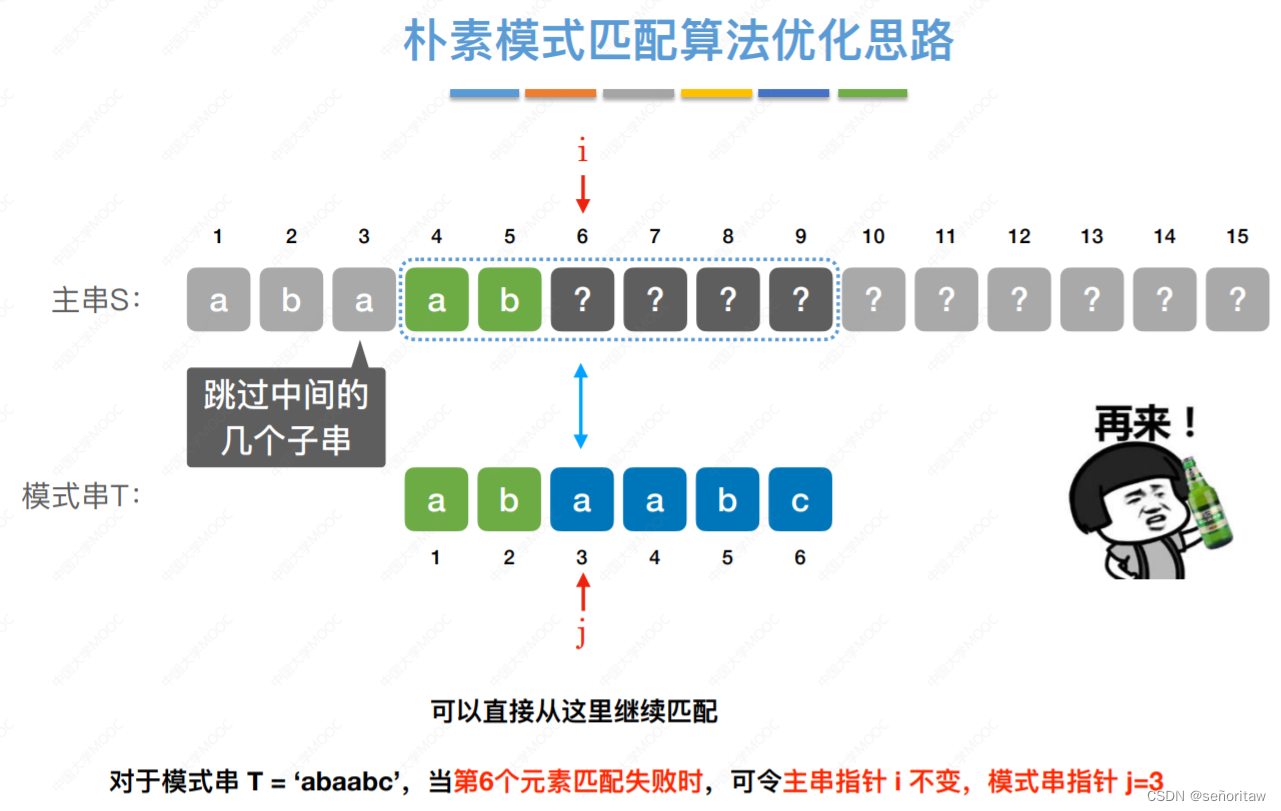
用代码实现这个处理逻辑 可以用一个next数组来存储让模式串指针指向的位置
next数组只和短短的模式串 有关,和长长的主串⽆关
KMP算法:当子串和模式串不匹配时,主串指针 i 不回溯,模式串指针 j=next[j]。
KMP算法最坏时间复杂度 O(m+n)
其中,求 next 数组时间复杂度 O(m)
模式匹配过程最坏时间复杂度 O(n)
KMP算法的代码实现
// 获取模式串T的next[]数组
void getNext(SString T, int next[]){
int i=1, j=0;
next[1]=0;
while(i<T.length){
if(j==0 || T.ch[1]==T.ch[j]){
++i; ++j;
next[i]=j;
}else
j=next[j];
}
}
// KPM算法,求主串S中模式串T的位序,没有则返回0
int Index_KMP(SString S, SString T){
int i=1, j=1;
int next[T.length+1];
getNext(T, next);
while(i<=S.length && j<=T.length){
if(j==0 || S.ch[i]==T.ch[j]){ //如果主串的元素和模式串的元素相等或j等于0时
++i;
++j; //i和j++,继续比较后继字符
}else
j=next[j]; //模式串向后移动
}
if(j>T.length)
return i-T.length; //j大于模式串长度说明匹配成功
else
return 0;
}
int main() {
SString S={"ababcabcd", 9};
SString T={"bcd", 3};
printf("%d ", Index_KPM(S, T)); //输出9
}
KMP算法精髓:利用已经匹配过的模式串的信息,求出next数组→利用next数组进行匹配(主串指针不回溯)
4.2.2_2_求next数组
next数组的作⽤:当模式串的第 j 个字符失配时,从模式串的第 next[j] 的继续往后匹配
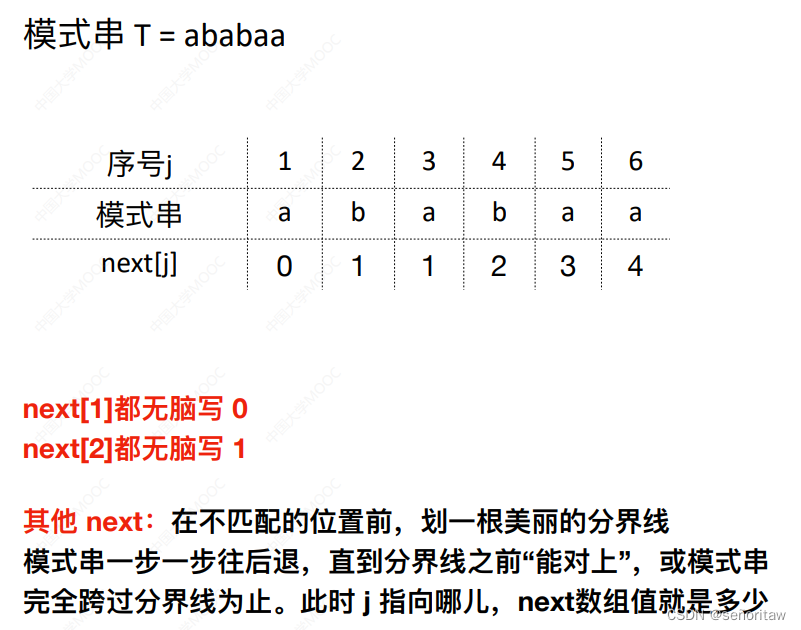
任何模式串第⼀个字符不匹配时,只能匹配下⼀个⼦串,因此,next[1]都⽆脑写 0
第2个字符不匹配时,应尝试匹配模式串的第1个字符, 因此,next[2]都⽆脑写 1
接下来的字符,在不匹配的位置前划一根分界线,模式串一步一步往后退,直到分界线前的“对的上”,或模式串完全越过分界线位置,如下面为第3个字符不匹配的情况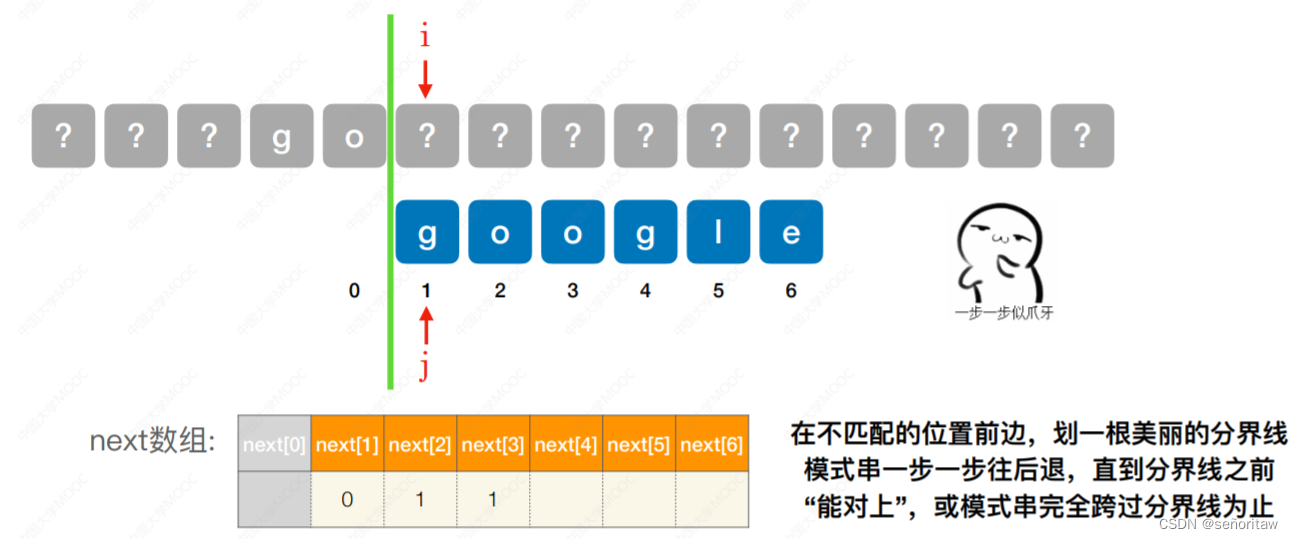 第四个字符不匹配
第四个字符不匹配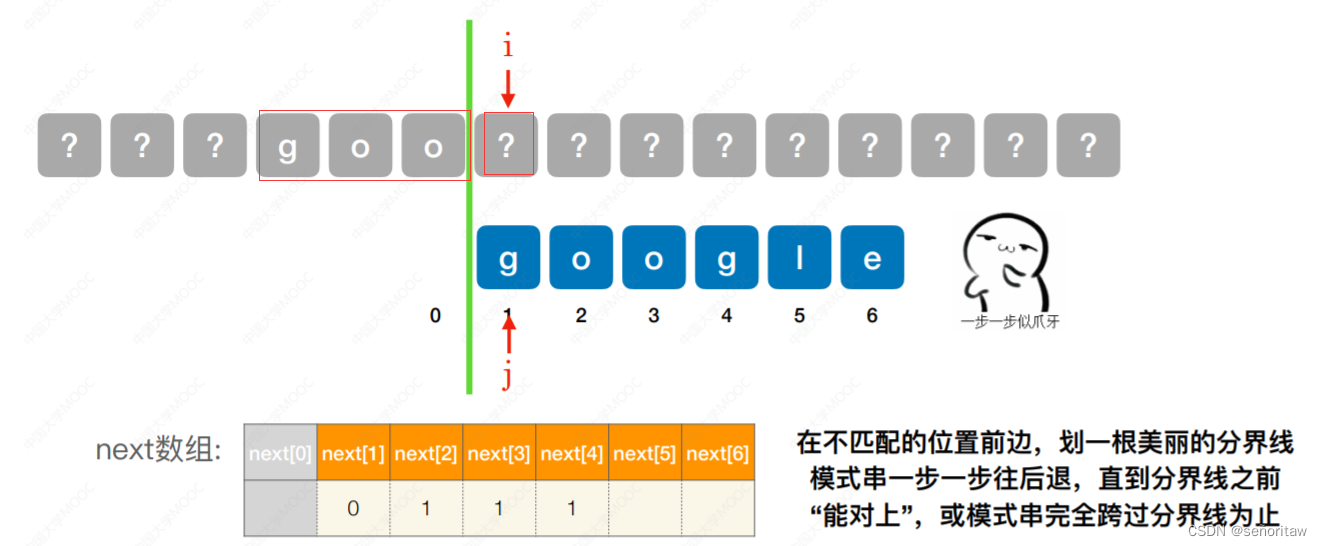
第五个字符不匹配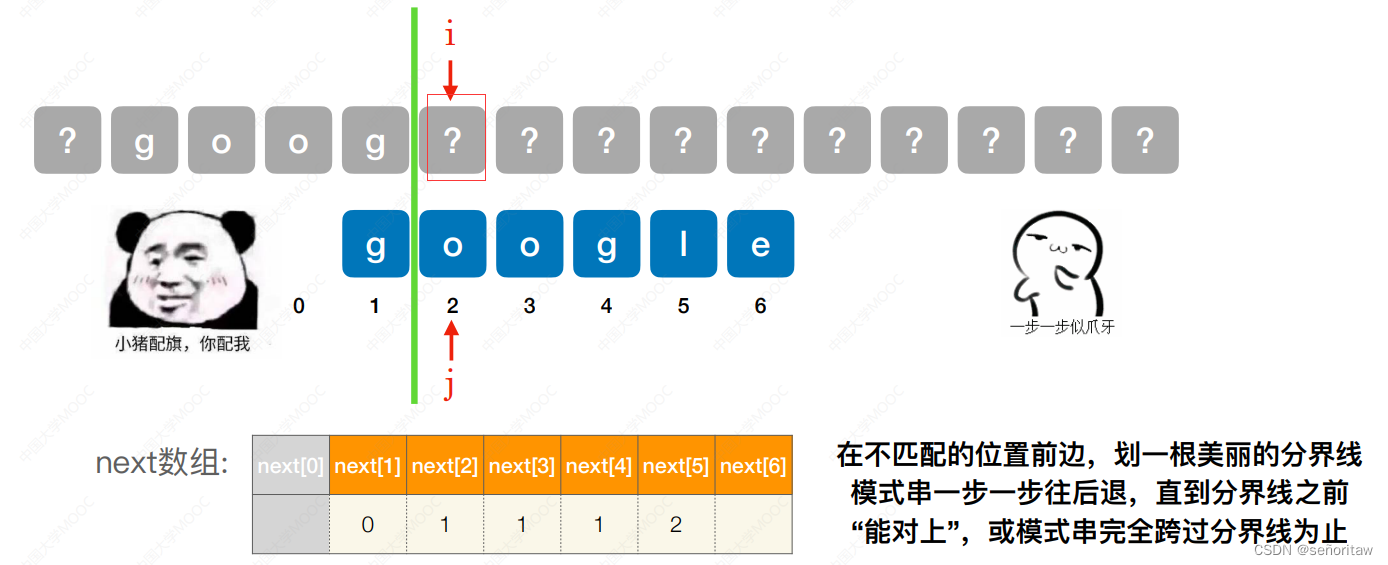
第六个字符不匹配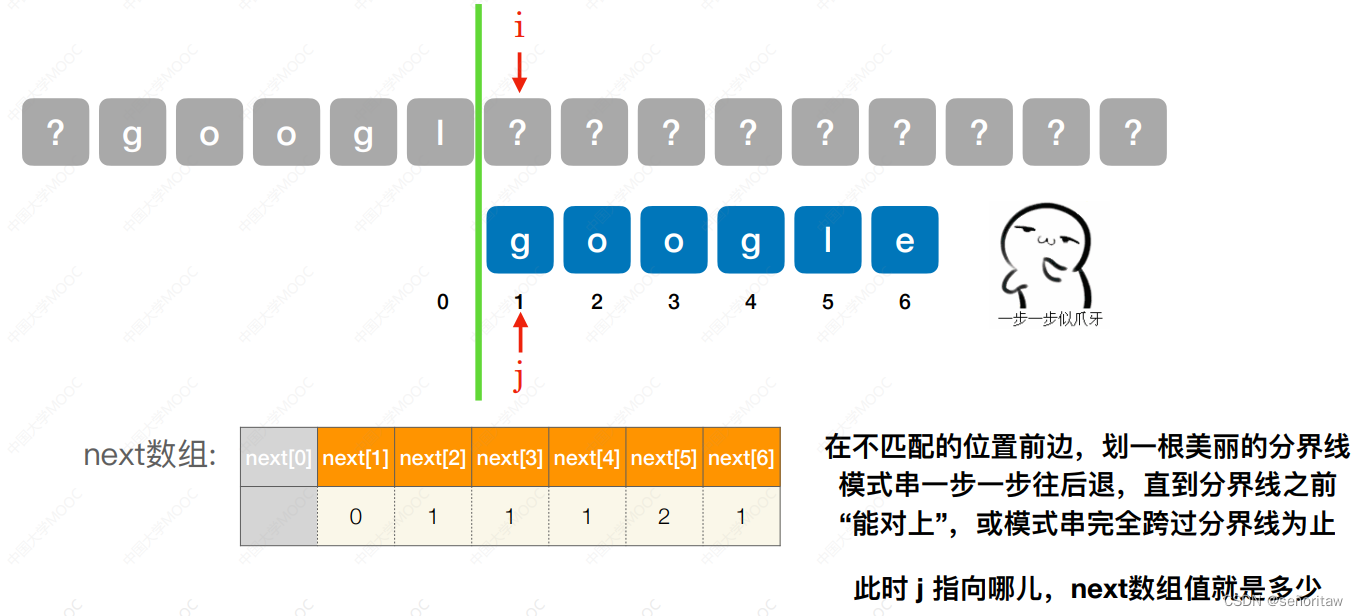
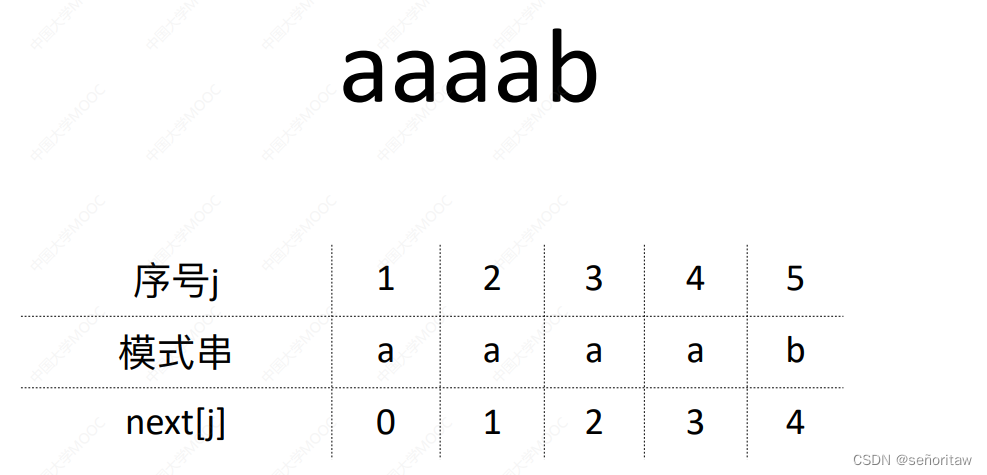
4.2.3_KMP算法的进一步优化
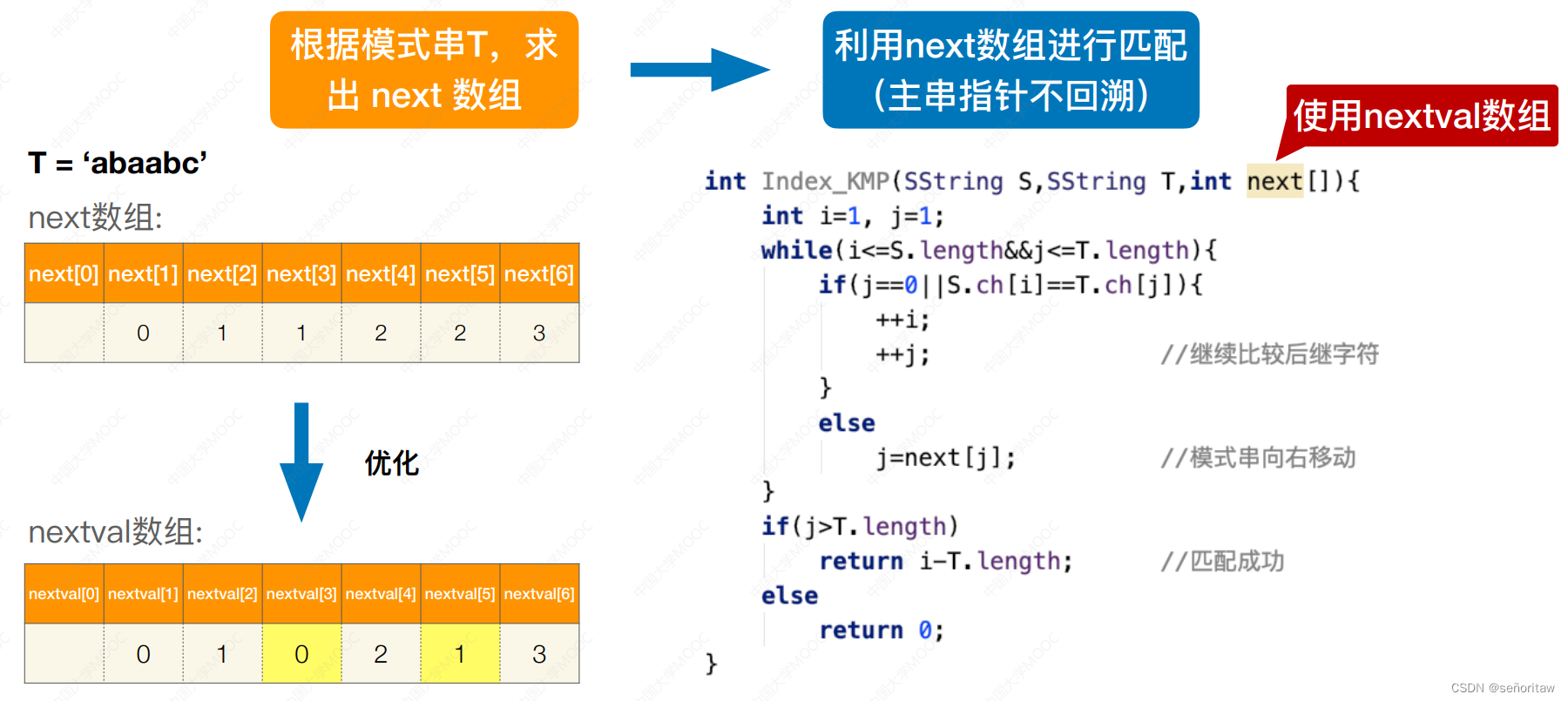
第3个字符和第1个字符相同,所以 可以直接跳到next[1]指向的位置,第5个字符跟第2个字符相同,直接跳到next[2]指向的位置
void getNextval(SString T, int nextval[]){
int i=1,j=0;
nextval[1]=0;
while(i<T.length){
if(j==0 || T.ch[i]==T.ch[j]){
++i; ++j;
if(T.ch[i]!=T.ch[j])
nextval[i]=j;
else
nextval[i]=nextval[j];
}else
j=nextval[j];
}
}



魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容







所有评论(0)