Verilog中的数据处理

一、数据表示

首先，我们要知道，在计算机中，对于数据的表示方式有三种：原码、补码、反码。

**原码：**将一个整数转换成二进制形式，就是其原码

**反码：**对于正数，它的反码就是其原码；

负数的反码是将二进制原码中除符号位以外的所有位（数值位）取反

**补码：**对于正数，它的补码就是其原码；

负数的补码是其反码加 1

为什么要这样设置呢？我们统一按照原码来计算不是很方便吗，也很好理解啊。之所以这样表示，是为了在二进制表示中有效地处理正负数，并简化电路的实现。

我们看到15，-15能很好的区分正数和负数。可是对于计算机而言，它看到是一串二进制，15的原码是01111，-15的原码是11111。原码在进行加减法运算时，计算机是无法区分正负的，如果不判断符号，计算结果就是错误的。必须先判断数的符号，再决定是加法还是减法，增加了运算的复杂性。

另外一个原因就是原码和反码中，0有两种表示形式（+0和-0）。在反码中，0仍然存在两种表示方式（+0为00000000，-0为11111111）。这在运算中带来了复杂性，因为你需要特别处理这两个不同的零。但是在补码中，对于正数+0，补码为00000000。对于负数-0，首先对正0取反得到11111111，然后加1得到00000000。

接下来举个例子来说明计算机中为何要用补码进行计算。比如计算$1-1$

原码计算：

1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = $-2$

反码计算：

1 - 1 = 1 + (-1) = [0000 0001]反 + [1111 1110]反 = [1111 1111]反 = [1000 0000]原 = $-0$

补码计算：

1 - 1 = 1 + (-1) =[0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原=0

二、有符号数与无符号数计算时的注意事项

1. 定义有符号数

• signed关键字：在Verilog中，使用signed关键字来声明一个有符号的变量或寄存器。例如：

  reg signed [7:0] a, b;
  

  如果没有使用signed关键字，Verilog默认认为变量是无符号的。在有符号数计算中，确保正确地使用signed声明变量，尤其是当变量需要参与带符号的运算时。

2. 确保运算双方的符号类型一致

如果有符号数与无符号数进行运算，Verilog会默认将操作数转为无符号数来进行计算，这可能导致错误的计算结果。尤其是当位宽不一样的时候。

所以我们可以使用$signed和$unsigned函数将变量显式转换为有符号或无符号。例如：

reg [7:0] a;
reg signed [8:0] signed_a;

signed_a = $signed(a);  // 将a转换为有符号数进行赋值

3. 符号扩展

当有符号数参与位宽不同的运算时，需要特别注意符号扩展。Verilog会在有符号数的符号位进行复制，以保持符号的正确性。

例如，对于8位有符号数a，在将其扩展为16位时，需要确保符号位被正确复制到高8位：

reg signed [7:0] a = -5;
reg signed [15:0] b;

b = a;  // 符号扩展，Verilog会自动将符号位复制

在这段代码中，将一个 8 位的有符号数 a 赋值给一个 16 位的有符号数 b。因为 b 的位宽比 a 大，所以在赋值过程中 Verilog 会对 a 进行符号扩展。

符号扩展的机制是：

• 保持原来的低 8 位数据不变。
• 用最高位（符号位）来填充剩下的高 8 位。

具体来说，a = -5 的二进制表示为 11111011（在 8 位补码中表示 -5，最高位 1 表示负数）。 当 a 被赋值给 b 时，Verilog 会执行符号扩展，使得 b 成为 16 位：

• 将 a 的符号位（最高位）扩展到 b 的剩余高位部分。
• 最终，b 的值会变成 11111111 11111011（16 位补码表示形式）。

符号扩展后，由补码变为原码时，符号位及符号扩展位均当作符号位进行处理。

4. 运算结果的位宽

在有符号数的运算中，运算结果的位宽需要特别关注。通常，两个有符号数相加时，运算结果的位宽应该比原来宽1位，以容纳可能的进位。

三、定点化数据处理

在FPGA里是无法直接使用浮点数进行计算的，因为计算机无法识别小数点。所以我们的加减乘除都是定点数计算（整数运算）。

定点数的定义就是小数点的位置固定，也就是小数的位宽是固定的。由于小数点的位置是固定的，所以就没有必要储存它（如果储存了小数点的位置，那就是浮点数了）。既然没有储存小数点的位置，那么计算机当然就不知道小数点的位置，所以这个小数点的位置是我们写程序的人自己需要牢记的！

我们一般把$2^N$量化等于1（单位1）。

比如10bit ，2^10=1，那么这里数值1表示的就是1/1024，转成浮点数就是1/1024=0.000976525。

如果要用6bit整数位，10bit小数位表示3.1415926。

3.1415926×1024=3214.0006≈3214

接下来，将 3214 转换为二进制表示：

$3214_{10}=110010001110_2$

这是一个 12 位的二进制数。我们用 16 位来表示这个定点数，其中前 6 位代表整数部分，后 10 位代表小数部分。因此在 Verilog 中，最终的 16 位表示为：

16’b0000_1100_1000_1110

1.位宽扩展

（1）加减法运算：扩位位宽=ceil（log2（加法或者减法个数））

（2）乘法运算：扩位位宽=两个乘数位宽的和

如：15bit数与14bit数相乘结果位宽应该为29bit

（3）除法运算：扩位位宽=被除数位宽与除数位宽的差

扩位时，对于有符号数，高位扩展时扩展符号位，对于无符号数高位扩展时直接补零。

因为有符号数高位是符号数，扩位补零会将负数扩展为错误的正数，而无符号数没有符号位，对位最高bit为1的无符号数，扩展符号位同样会导致数据异常。

//符号位扩展
assign s_data_a = {i_data_a[data_width-1],i_data_a};
assign s_data_b = {i_data_b[data_width-1],i_data_b};

2.高位截位

一般来说，截高位通常用于截取掉信号过多的符号位，在我们确认该数据确实不需要这么宽的位宽时，直接可以把高位符号位去掉，这个时候该信号的幅值不会发生任何变化。

（1）直接截位：直接抛弃高位保留低位，高位直接截位，低位四舍五入输出。在确认信号不会溢出的模块使用直接截位的方法，节省资源

wire [15:0] A;  // 原始定点数
wire [7:0] B;

// 保留低 8 位
assign B = A[7:0];

（2）饱和截位：对计算后的数据进行判断，如果超过位宽，正数输出为最大值，负数输出为最小值；判断方法就是看高位是否完全相同

3.低位截位

这是Vivado提供的一些低位截位方法，我们对这些方法进行分析。

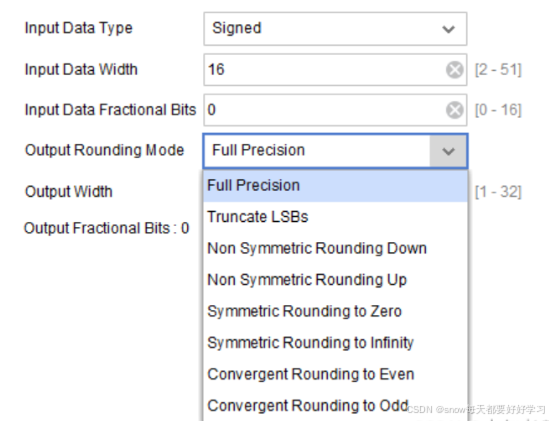
Full Precision (全精度)

保持全部的位宽，不执行任何截位或舍入操作。这意味着所有的输入位都会保留，不会丢弃任何信息。

Truncation（截断低有效位）

直接丢弃低位数据而不进行舍入，保留高位。这种方法快速且简单，但可能引入误差，尤其是在需要高精度的计算中。

module truncate_lsbs(
    input signed [15:0] in,
    output signed [11:0] out
);
    assign out = in[15:4];  // 丢弃低 4 位
endmodule

示例： 输入 in = 16'b0000_0000_1001_1011 (+155)，输出 out = 12'b0000_1001 (+9)。

Non Symmetric Rounding Down（非对称向下舍入）

将值向下舍入到最近的整数。对于定点数，可以将小数部分直接丢弃，等价于向下取整。例如，3.7会变为3。

assign result = input_data >> m; // m 是小数位数

Non Symmetric Rounding Up（非对称向上舍入）

将值向上舍入到最近的整数。例如，3.2会变为4。

assign result = (input_data + (1 << (m - 1))) >> m; // m 是小数位数

Symmetric Rounding to Zero（对称向零舍入）

正数向下舍入，负数向上舍入。例如，+3.7舍入为3，-3.7舍入为-3。相当于舍弃小数部分。此方法可用于减少偏差，因为正负方向的值都会朝零的方向靠拢。

assign result = input_data >> m; // m 是小数位数

Symmetric Rounding to Infinity（对称向无穷大舍入）

正数向上舍入，负数向下舍入。例如，+3.2舍入为4，-3.2舍入为-4。通常用于尽量保留数值范围的场景。

//假设我们有一个 16 位宽的输入数据 input_data，表示为 16'b0000010010011000，即十进制数 1176。我们要对这个数据进行舍入操作。假设 input_data 的低 4 位是小数位（也就是说，我们的定点数格式是 12 位整数加 4 位小数）。
module round_to_infinity (
    input [15:0] input_data,
    output [11:0] result
);
    assign result = (input_data[15] ? (input_data - 16'd8) : (input_data + 16'd8)) >> 4;  // 符号位判断
endmodule

Convergent Rounding to Even（趋近向偶数舍入）

当遇到正好位于中间的值（例如0.5）时，舍入到最接近的偶数。例如，2.5舍入为2，而3.5舍入为4。这种方法能够减少累积误差，是统计上常用的舍入方式。

module round_to_even (
    input [15:0] input_data,
    output [11:0] result
);
    wire [3:0] lsb = input_data[3:0];
    wire round_bit = (lsb > 4'd8) || ((lsb == 4'd8) && (input_data[4] == 1));
    assign result = (input_data >> 4) + round_bit;
endmodule

Convergent Rounding to Odd（趋近向奇数舍入）

类似于向偶数舍入，但中间值将舍入到最接近的奇数。例如，2.5舍入为3，3.5舍入为3。这种方式较为少见，但在特定场景下也有应用。

module round_to_odd (
    input [15:0] input_data,
    output [11:0] result
);
    wire [3:0] lsb = input_data[3:0];
    wire round_bit = (lsb > 4'd8) || ((lsb == 4'd8) && (input_data[4] == 0));
    assign result = (input_data >> 4) + round_bit;
endmodule