多速率数据处理
采样的原理是:x(n)=xc(t)∣t=nT=xc(nT),xc(t)x(n)=x_c(t)|_{t=nT}=x_c(nT),x_c (t)x(n)=xc(t)∣t=nT=xc(nT),xc(t)是连续时间信号。x(n)x(n)x(n)是相应的离散时间信号。T是采样率。Xc(Ω)是xc(t)X_c(Ω)是x_c(t)Xc(Ω)是xc(t)的连续时间傅里叶变换。X(ΩT)=1/T(∑(k
1. 多速率数据处理
采样的原理是:x(n)=xc(t)∣t=nT=xc(nT),xc(t)x(n)=x_c(t)|_{t=nT}=x_c(nT),x_c (t)x(n)=xc(t)∣t=nT=xc(nT),xc(t)是连续时间信号。x(n)x(n)x(n)是相应的离散时间信号。T是采样率。
Xc(Ω)是xc(t)X_c(Ω)是x_c(t)Xc(Ω)是xc(t)的连续时间傅里叶变换。
X(ΩT)=1/T(∑(k=0)∞Xc(Ω−2πk/T))X(ΩT)=1/T(\sum_{(k=0)}^{∞}X_c (Ω-2πk/T))X(ΩT)=1/T(∑(k=0)∞Xc(Ω−2πk/T))
X(w)=1/T(∑(k=0)∞Xc(W/T−2πk/T))X(w)= 1/T(\sum_{(k=0)}^{∞}X_c (W/T-2πk/T))X(w)=1/T(∑(k=0)∞Xc(W/T−2πk/T))
1.1抽取
1.1.1 抽取原理
抽取是把原始的采样数据每隔M-1个取一个,形成新的采样序列,其中M为大于1的整数,称为抽取因子,实现这一过程的装置称为M-抽取器,所以输入数据的采样率为fs=1/T,输出数据的采样率为fs2=fs/M=xd[n]/(MT)=x(nM)f_{s2}=f_s/M=x_d [n]/(MT)=x(nM)fs2=fs/M=xd[n]/(MT)=x(nM)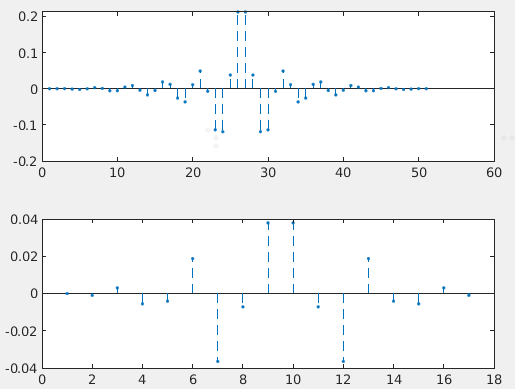
如果要采样不产生混叠,则x(n)x(n)x(n)的频率限制在fs/2{f_s}/2fs/2以内,以因子M进行抽取后不产生混叠的频率范围为fs/(2M)f_s/(2M)fs/(2M)如果x(n)x(n)x(n)中含有大于fs/(2M)f_s/(2M)fs/(2M)的频率分量,必然产生频谱混叠,导致不能从xd[n]x_d [n]xd[n]中恢复x(n).
与模拟信号采样类似,原始采样后的信号x[n]=xc(nT)x[n]=x_c(nT)x[n]=xc(nT),经过M倍下采样后为:
xd[n]=xc[nT′]=xc[nMT]=x[nM],T′=MTx_d [n]=x_c[nT']=x_c[nMT]=x[nM],T'=MTxd[n]=xc[nT′]=xc[nMT]=x[nM],T′=MT,
采样周期变长,采样率变为原来的1/M倍,
xint[n]={x(n),n=0,±M,±2M,….0,n=其他(1) x_{int} [n]= \begin{cases} x(n),\quad n=0,±M,±2M,….\\ 0, \quad n=其他 \end{cases} \tag{1} xint[n]={x(n),n=0,±M,±2M,….0,n=其他(1)
xint[n]=x(n)∑(i=−∞)∞δ(n−iM)=x(n)∙δD(n)其中δD(n)=∑(i=−∞)∞δ(n−iM)xd[n]=xint[nM]=x(nM)x_{int} [n]=x(n)\sum_{(i=-∞)}^∞δ(n-iM)=x(n)∙δ_D (n)\\ 其中δ_D (n)=\sum_{(i=-∞)}^∞δ(n-iM) x_d [n]=x_{int} [nM]=x(nM)xint[n]=x(n)(i=−∞)∑∞δ(n−iM)=x(n)∙δD(n)其中δD(n)=(i=−∞)∑∞δ(n−iM)xd[n]=xint[nM]=x(nM)
Xd(ejw)=∑(n=−∞)∞xd[n]e(−jwn)=∑(n=−∞)∞x[nM]e(−jwn)=∑(n=−∞)∞xint[nM]e(−jwn)=∑(m=−∞)∞xint[m]e((−jwm)/M) X_d {(e^{jw})}=\sum_{(n=-∞)}^∞x_d [n] e^{(-jwn)}=\sum_{(n=-∞)}^∞x[nM]e^{(-jwn)}\\ =\sum_{(n=-∞)}^∞x_{int} [nM] e^{(-jwn)}=\sum_{(m=-∞)}^∞x_{int}[m]e^{({(-jwm)}/M)}Xd(ejw)=(n=−∞)∑∞xd[n]e(−jwn)=(n=−∞)∑∞x[nM]e(−jwn)=(n=−∞)∑∞xint[nM]e(−jwn)=(m=−∞)∑∞xint[m]e((−jwm)/M)
上式中,令nM=m,n=m/M,m是M的整数倍,由于m不是M的整数倍时,xint[n]为0。nM=m,n=m/M ,m是M的整数倍,由于m不是M的整数倍时,x_{int} [n]为0。nM=m,n=m/M,m是M的整数倍,由于m不是M的整数倍时,xint[n]为0。
Xd(ejw)=∑(m=−∞)∞xint[m]e(−jwm/M)=∑(m=−∞)∞x(m)δD(m)e(−jwm/M)X_d(e^{jw})=\sum_{(m=-∞)}^∞x_{int} [m]e^{(-jwm/M)}=\sum_{(m=-∞)}^∞x(m)δ_D (m)e^{(-jwm/M)}Xd(ejw)=(m=−∞)∑∞xint[m]e(−jwm/M)=(m=−∞)∑∞x(m)δD(m)e(−jwm/M)
1/M∑(r=0)(M−1)WM(−mr)={1,m=iM,±2M,….0,m=其他(2) 1/M\sum_{(r=0)}^{(M-1)}W_M^{(-mr)}= \begin{cases} 1,\quad m=iM,±2M,….\\ 0, \quad m=其他 \end{cases} \tag{2} 1/M(r=0)∑(M−1)WM(−mr)={1,m=iM,±2M,….0,m=其他(2)
所以:
Xd(ejw)=∑m=−∞∞x(m)⋅1M∑(r=0)(M−1)WM(−mr)e(−jwm/M)=1/M∑r=0M−1∑(m=−∞)∞x(m)[WM(−mr)e(−jwm/M)]X_d {(e^{jw})} =\sum_{m=-∞}^∞x(m)\cdot{\frac1M }∑_{(r=0)}^{(M-1)}W_M^{(-mr)} e^{(-jwm/M)} =1/M \sum_{r=0}^{M-1}\sum_{(m=-∞)}^∞x(m)[W_M^{(-mr)} e^{(-jwm/M)}]Xd(ejw)=∑m=−∞∞x(m)⋅M1∑(r=0)(M−1)WM(−mr)e(−jwm/M)=1/M∑r=0M−1∑(m=−∞)∞x(m)[WM(−mr)e(−jwm/M)]
=1/M∑r=0M−1∑(m=−∞)∞x(m)[WMre(jw/M)]−m=1/M∑r=0M−1X(WMre(jw/M))=1/M \sum_{r=0}^{M-1}\sum_{(m=-∞)}^∞x(m){[W_M^{r} e^{(jw/M)}]}^{-m} =1/M \sum_{r=0}^{M-1}X(W_M^r e^{(jw/M)})=1/M∑r=0M−1∑(m=−∞)∞x(m)[WMre(jw/M)]−m=1/M∑r=0M−1X(WMre(jw/M))
=1/M∑r=0M−1∑(m=−∞)∞x(m)[e(−j2πr/M)e(jw/M)](−m)=1/M \sum_{r=0}^{M-1}\sum_{(m=-∞)}^∞x(m){[e^{(-j2πr/M)} e^{(jw/M)} ]}^{(-m)}=1/M∑r=0M−1∑(m=−∞)∞x(m)[e(−j2πr/M)e(jw/M)](−m)
=1/M∑r=0M−1∑(m=−∞)∞x(m)[e(j(w−2πr))/M)](−m)=1/M \sum_{r=0}^{M-1}\sum_{(m=-∞)}^∞x(m) {[e^{(j(w-2πr))/M) }]}^{(-m)}=1/M∑r=0M−1∑(m=−∞)∞x(m)[e(j(w−2πr))/M)](−m)
Xd(ejw)=X(ej(w−2πr)M)X_d (e^{jw})=X(e^{\frac {j (w-2πr)}M})Xd(ejw)=X(eMj(w−2πr))
(w−2πr)/M=2π,周期扩展成2πM倍(w-2πr)/M=2π,周期扩展成2πM倍(w−2πr)/M=2π,周期扩展成2πM倍,Xd(z)=1/M∑r=0M−1X(WMrz1M)X_d (z)=1/M \sum_{r=0}^{M-1}X(W_M^r z^{\frac1M})Xd(z)=1/M∑r=0M−1X(WMrzM1)
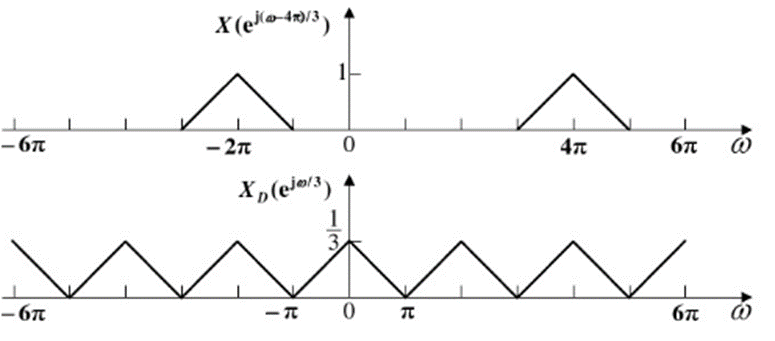
可见,抽取序列的频谱Xd(ejw)是原序列频谱M倍展宽后按(2π)的整数倍位移并叠加而成.可见,抽取序列的频谱X_d (e^jw )是原序列频谱M倍展宽后按(2π)的整数倍位移并叠加而成.可见,抽取序列的频谱Xd(ejw)是原序列频谱M倍展宽后按(2π)的整数倍位移并叠加而成.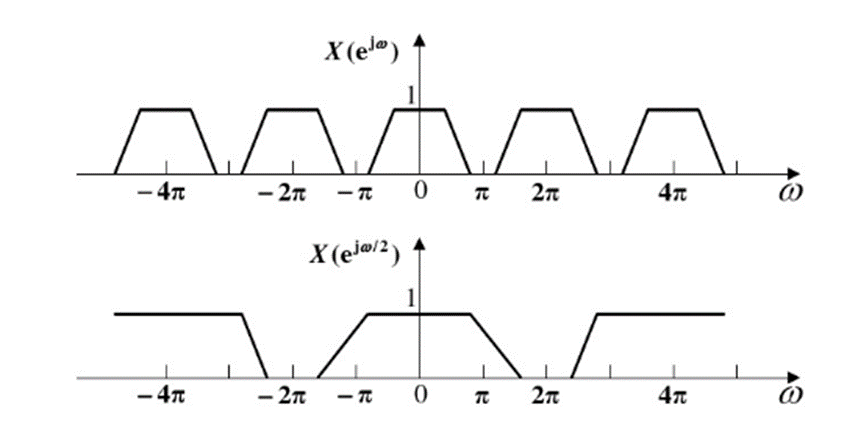
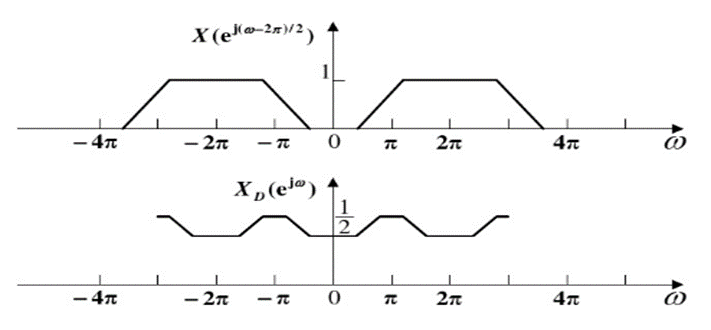
Xd(ejw)X_d (e^{jw})Xd(ejw)是一些平移样本之和,信号经过M倍抽取后频带会扩展为原来的M倍,如果输入信号x(n)不是带限信号,则YD(ejw)Y_D (e^{jw})YD(ejw)频谱会发生混叠,这样就无法从叠加信号中恢复出原始信号x(n),为了避免抽取后的频谱混叠,信号x(n)的带宽必须限制在[−π/M,π/M][-π/M,π/M][−π/M,π/M]中,通常采取抗混叠滤波在抽取之前对信号进行低通滤波处理,把信号频谱限制在[−π/M,π/M][-π/M,π/M][−π/M,π/M]范围内。信号抽取后的极限速度是奈奎斯特采样频率,即最高频率的2倍。
若原信号x(t)频带宽度ΩsΩ_sΩs,经过采样率Fs(采样周期Ts)采样后为x(n),x(n)的频带宽度Wx=Ωs,Ts=Ωs/FsW_x=Ω_s, Ts=Ω_s/F_sWx=Ωs,Ts=Ωs/Fs,经过M倍抽取后,新的采样率为Fs/MF_s/MFs/M(采样周期为MTsMT_sMTs),所以M倍抽取后新的频带宽度为Wy=MΩsTsW_y=MΩ_s T_sWy=MΩsTs,显然通过下采样过程,频率区间0≤∣W∣≤Wx=ΩsTs扩展到0≤∣W∣≤Wy=MΩsTs0≤|W|≤W_x=Ω_s T_s扩展到0≤|W|≤W_y=MΩ_s T_s0≤∣W∣≤Wx=ΩsTs扩展到0≤∣W∣≤Wy=MΩsTs,所以若原频率区间为0≤∣W∣≤π/M0≤|W|≤π/M0≤∣W∣≤π/M,则新的频率区间为0≤∣W∣≤π0≤|W|≤π0≤∣W∣≤π.
如果在抽取前先用一数字低通滤波器(滤波器的带宽为π/Mπ/Mπ/M,对x(n)进行滤波,使得X(ejw)=0,∣W∣>π/MX(e^{jw})=0, |W|>π/MX(ejw)=0,∣W∣>π/M, 则按因子M抽取后信号频谱不会发生混叠,序列抽取不发生混叠的Nyquist条件.
∣HD(ejw)∣={M,∣w∣<π/M0,其他(3) |H_D (e^{jw})|= \begin{cases} M,\quad |w|<π/M\\ 0, \quad 其他 \end{cases} \tag{3} ∣HD(ejw)∣={M,∣w∣<π/M0,其他(3)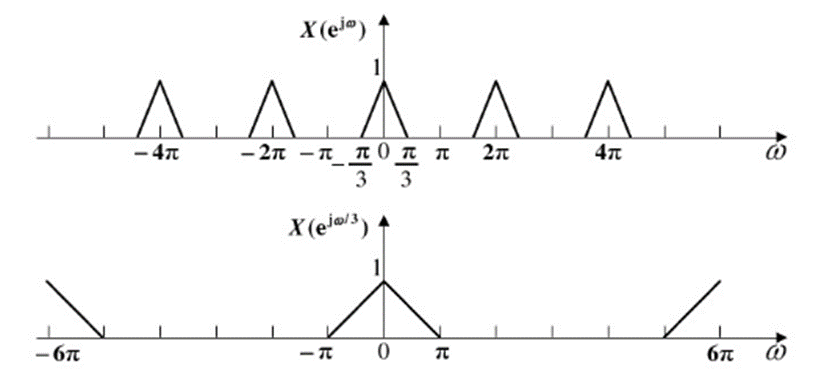
1.2 matlab程序
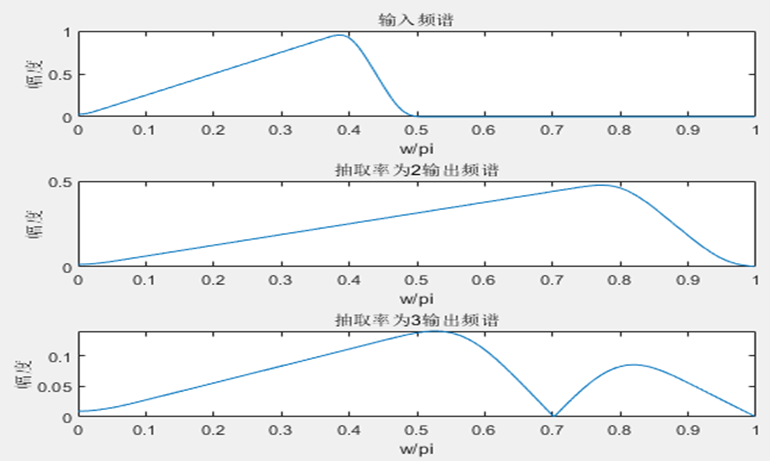
用matlab对抽取所造成的的信号频谱混叠与不混叠这两种情况的仿真。
freq=[0 0.4 0.48 1];
mag=[0 1 0 0];
x=fir2(99,freq,mag); %输入
[xz,w]=freqz(x,1,512);
subplot(3,1,1);
plot(w/pi,abs(xz));
xlabel(‘w/pi’);ylabel(‘幅度’);title(‘输入频谱’);
M=2; %抽取率为2
y=x(1:M:length(x));
[yz,w]=freqz(y,1,512);
subplot(3,1,2);
plot(w/pi,abs(yz));
xlabel(‘w/pi’);ylabel(‘幅度’);title(‘抽取率为2输出频谱’);
M=3; %抽取率为3
y=x(1:M:length(x));
[yz,w]=freqz(y,1,512);
subplot(3,1,3);
plot(w/pi,abs(yz));
xlabel(‘w/pi’);ylabel(‘幅度’);title(‘抽取率为3输出频谱’);
1.3 verilog程序
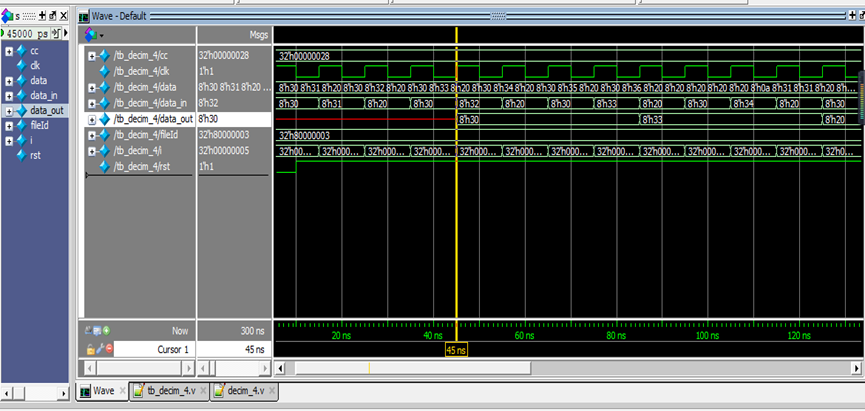
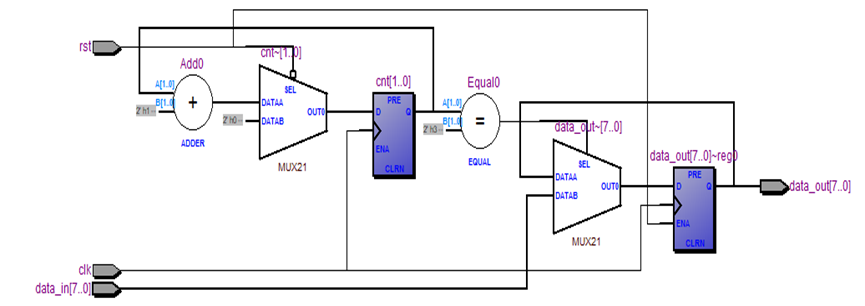
verilog实现输入数据的4倍抽取
利用输入数据数据信号时钟的4倍分频,利用该低速时钟采样输入数据。
`timescale 1ns / 1ps
module decim_4(
input clk,
input rst,
input [7:0]data_in,
output reg[7:0]data_out
);
reg [1:0]cnt;
always @(posedge clk)
begin
if(!rst)
cnt <= 0;
else begin
cnt <= cnt + 1;
if(cnt == 2'b11)
data_out <= data_in;
else
data_out <= data_out;
end
end
endmodule
1.4 内插
数字信号的频谱是周期性的,且周期等于数据的采样频率。整数倍零值内插显然不能简单等同于提高了数据的采样频率。
内插就是在已知序列x(n)的相邻采样点之间等间距的插入L-1个0值点,L为大于1的整数,称为内插因子,实现这一过程的系统称为L内插器,其中输入采样率为f=1/T,输出采样率为f=L/T。

原始采样后的信号x[n]=xc(nT)x[n]=x_c(nT)x[n]=xc(nT),经过L倍增采样后为:
xi[n]=xc[nT′]=xc[nT/L],T′=T/Lx_i [n]=x_c[nT']=x_c[nT/L],T'=T/Lxi[n]=xc[nT′]=xc[nT/L],T′=T/L,采样周期变短,采样率变为原来的L倍,当n=kL(kn=kL(kn=kL(k为整数), xi[n]=x[n/L]=∑k=−∞∞x[k]δ[n−kL],其他情况为xi[n]=0x_i [n]=x[n/L]= \sum_{k=-∞}^∞x[k]δ[n-kL],其他情况为x_i [n]=0xi[n]=x[n/L]=∑k=−∞∞x[k]δ[n−kL],其他情况为xi[n]=0;
XI(ejw)=∑n=−∞∞∑k=−∞∞(x[k]δ[n−kL])e(−jwn)=∑k=−∞∞x[k]e(−jwkL)=X(ejwL)X_I (e^{jw}) =\sum_{n=-∞}^∞\sum_{k=-∞}^∞(x[k]δ[n-kL]) e^{(-jwn)}=\sum_{k=-∞}^∞x[k]e^{(-jwkL)}=X(e^{jwL})XI(ejw)=∑n=−∞∞∑k=−∞∞(x[k]δ[n−kL])e(−jwn)=∑k=−∞∞x[k]e(−jwkL)=X(ejwL)
XI(z)=X(zL)X_I (z)=X(z^L)XI(z)=X(zL)
XI(ejw)中不仅X(ejw)X_I (e^{jw})中不仅X(e^{jw})XI(ejw)中不仅X(ejw)的基带部分,还含有大于π/L的高频成分。
内插后信号频谱被压缩了L倍,XI(ejw)=X(ejwL),XI(ejw)是对X(ejw)X_I (e^{jw})= X(e^{jwL}), X_I (e^{jw})是对X(e^{jw})XI(ejw)=X(ejwL),XI(ejw)是对X(ejw)频谱的L倍压缩,即内插后频谱的周期变为原来的1/L,因此在数字频率轴上,2π范围内会产生重复的波形,称为镜像。所以对频谱内插,要保证序列的原始特性不变,需要在内插后接一个低通滤波器滤除[−π/L,π/L][-π/L,π/L][−π/L,π/L]之外的频谱,以消除内插带来的镜像。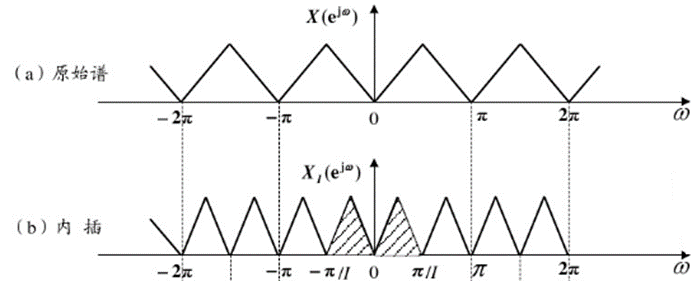
为了能从中XI(ejw)X_I (e^{jw})XI(ejw)得到基带信号,需要通过低通濾波消除内插带来的镜像。低通滤波器的幅度响应为
同理,内插与抽取相反:若原信号x(t)频带宽度Ωs,经过采样率Fs(采样周期Ts)采样后为x(n),x(n)x(t)频带宽度Ω_s,经过采样率F_s(采样周期T_s)采样后为x(n),x(n)x(t)频带宽度Ωs,经过采样率Fs(采样周期Ts)采样后为x(n),x(n)的频带宽度Wx=ΩsTs=Ωs/FsW_x=Ω_s T_s=Ω_s/F_sWx=ΩsTs=Ωs/Fs,经过M倍内插后,新的采样率为LFs(采样周期为Ts/LT_s/LTs/L),所以L倍内插后新的频带宽度为Wy=ΩsTs/LW_y=Ω_s T_s/LWy=ΩsTs/L,显然通过上采样过程,频率区间0≤∣W∣≤Wx=ΩsTs0≤|W|≤W_x=Ω_sT_s0≤∣W∣≤Wx=ΩsTs压缩到0≤∣W∣≤Wy=ΩsTs/L0≤|W|≤W_y=Ω_s T_s/L0≤∣W∣≤Wy=ΩsTs/L,所以若原频率区间为0≤∣W∣≤π0≤|W|≤π0≤∣W∣≤π,则新的频率区间为0≤∣W∣≤π/L0≤|W|≤π/L0≤∣W∣≤π/L.
∣HI(ejw)∣={1,∣w∣<π/L0,其他(4) |H_I(e^{jw})|= \begin{cases} 1,\quad |w|<π/L\\ 0, \quad 其他 \end{cases} \tag{4} ∣HI(ejw)∣={1,∣w∣<π/L0,其他(4)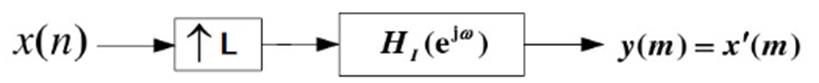
1.4 matlab程序
用matlab对内插所造成的的信号频谱混叠与不混叠这两种情况的仿真。
freq=[0 0.4 0.48 1];
mag=[0 1 0 0];
x=fir2(99,freq,mag); %输入
[xz,w]=freqz(x,1,512);
subplot(2,1,1);
plot(w/pi,abs(xz));
xlabel('w/pi');ylabel('幅度');title('输入频谱');
L=2; %内插因子为2
y=zeros(1,L*length(x));
y([1:L:length(y)])=x;
[yz,w]=freqz(y,1,512);
subplot(2,1,2);
plot(w/pi,abs(yz));
xlabel('w/pi');ylabel('幅度');title('内插率为2的输出频谱');
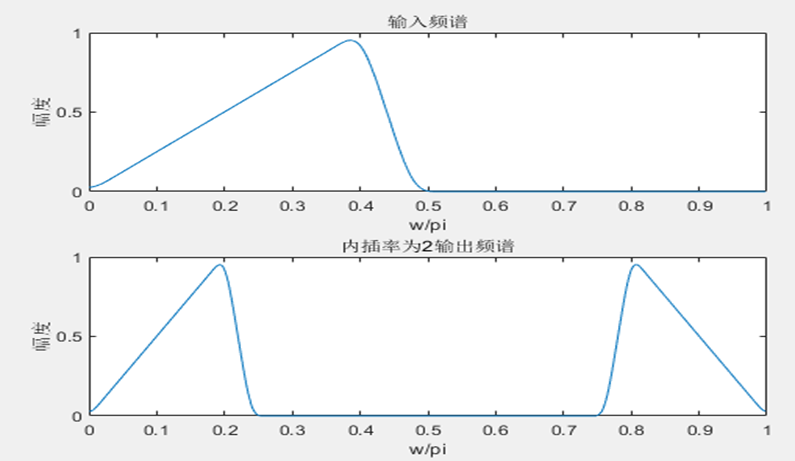
经过内插后,信号的频谱相对而言变得更窄,也就意味着可以看到更宽的信号带宽。
1.4.1 matlab整数倍内插
用matlab仿真整数倍内插过程的信号变换关系。
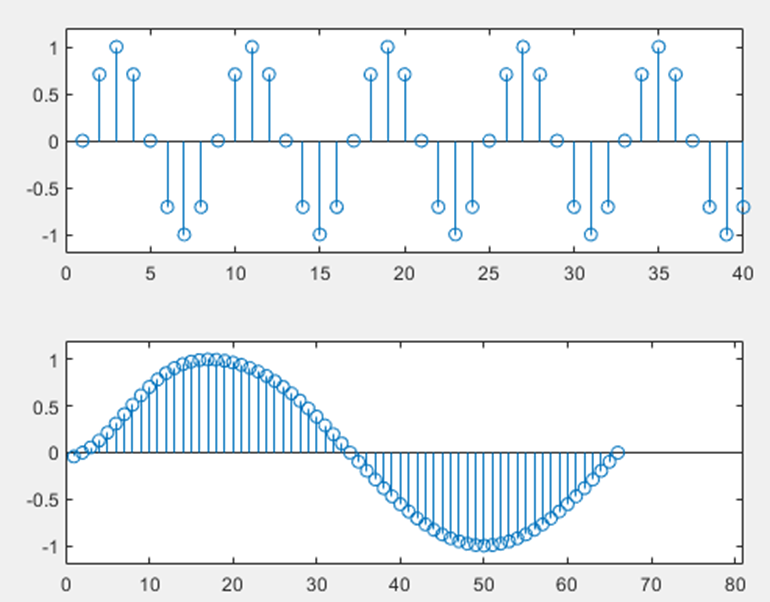
假设原始信号为频率为100hz的正弦波,初始采样频率为800hz,仿真对信号进行8倍内插后的信号波形图,比较内插前后信号的时域波形变化。
f=100; %信号频率为100hz
fs=800; %采样频率为800hz
N=400; %采样个数
I=8; %内插倍数
%产生信号
t=0:1/fs:(N-1)/fs;
si=sin(2*pi*f*t);
%进行8倍零值内插处理
Isi=zeros(1,length(si)*I);
lsi(1:I: length(Isi))=si;
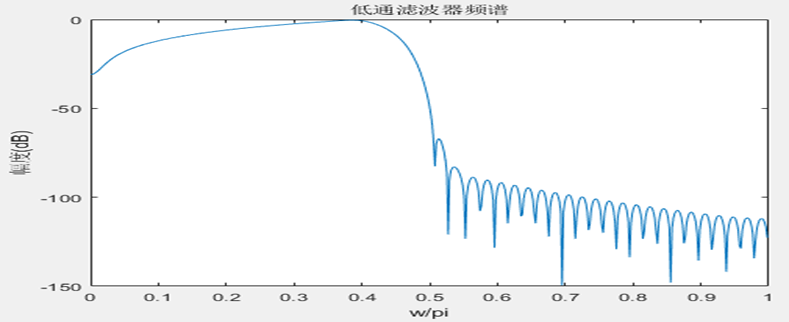
%经低通滤波器处理
b=fir1(80,1/I);
[bz,w]=freqz(b,1,512);
figure;
plot(w/pi,20*log10(abs(xz)));
xlabel('w/pi');ylabel('幅度(dB)');title('低通滤波器频谱');
filterS=filter(b,1,Isi);
filterS=filterS/max(abs(filterS));
%画图
figure;
subplot(211);stem(si(1:400));axis([0 40 -1.2 1.2]);
subplot(212);stem(filterS(1:80));axis([0 80 -1.2 1.2]);
Verilog实现整数倍4倍内插
module interpolate4(clk, rst, data_in, data_out);
input clk;
input rst;
input [7:0]data_in;
output [7:0]data_out;
reg [7:0]data_out;
reg [1:0] cnt;
always @(posedge clk) begin //完成内插
if(!rst)
cnt <= 0;
else begin
cnt <= cnt +1;
if(cnt == 0)
data_out<= data_in;
else
data_out<=0;
end
end
endmodule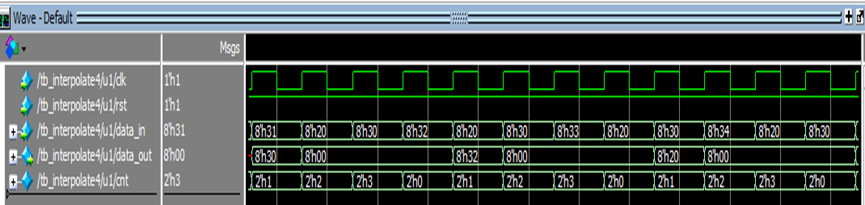
1.5抽取内插后频带变换
1.5.1抽取
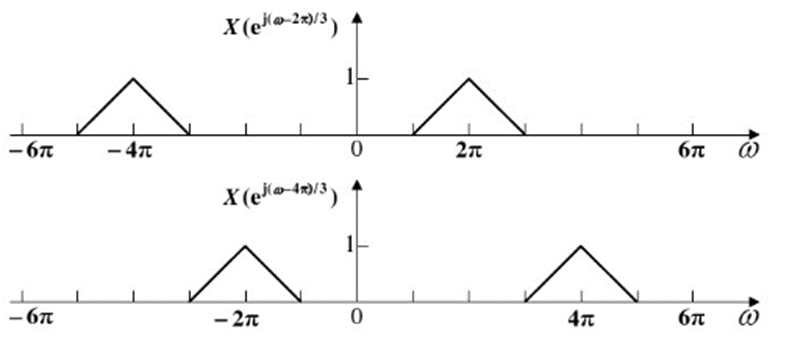
假设信号带宽为[-4khz,4khz],Fs为16khz,信号范围为[-Fs/4, Fs/4],满足图2上的要求,2倍抽取后,数据采样率为Fs’=8khz,图2下对应信号频带范围为:[-Fs’/2, Fs’/2],对应的信号频带范围仍为[-4khz,4khz],所以采样率发生变化,信号频带范围不发生变化,只是采样率发生变化,对采样频率归一化后的信号相对带宽发生变化。原来的频谱周期为Fs,现在的频谱周期变为Fs’。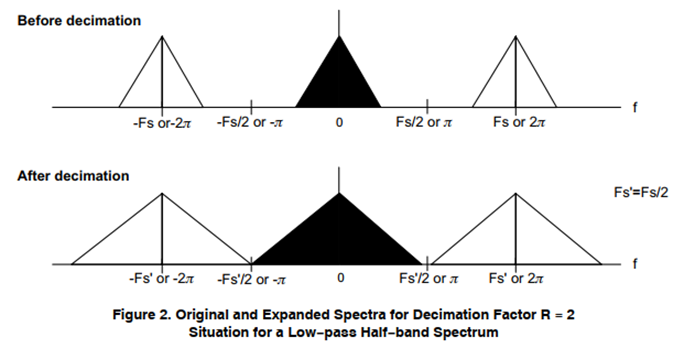
1.5.2 内插
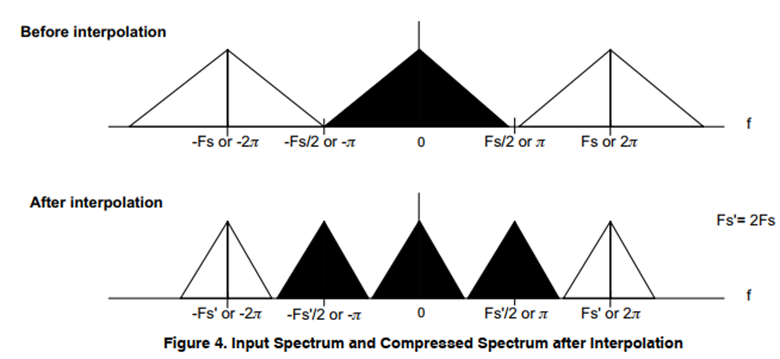
假设信号带宽为[-4khz,4khz],Fs为8khz,信号范围为[-Fs/2, Fs/2],满足图4上的要求,2倍内插后,数据采样率为Fs’=16khz,
图2下对应信号频带范围为:[-Fs’/4, Fs’/4],对应的信号频带范围仍为[-4khz,4khz],所以虽然采样率发生变化,信号频带范围不发生变化,只是采样率发生了变化,信号的频带范围相对采样率发生了变化,对采样频率归一化后的信号相对带宽发生变化。但是原来的频谱周期为Fs,内插后频谱的周期变为Fs’/2.会在频谱周期内产生重复的频谱图形。
1.6 Nobel恒等变换
1.6.1抽取
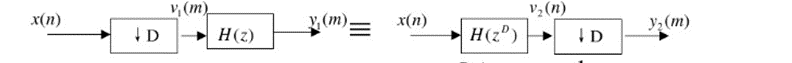
Xd(z)=1/M∑r=0M−1X(WMrz(1/M))X_d (z)=1/M \sum_{r=0}^{M-1}X(W_M^r z^{(1/M)})Xd(z)=1/M∑r=0M−1X(WMrz(1/M))
V1(z)=1/M∑r=0M−1X(WMrz(1/M))V_1 (z)=1/M \sum_{r=0}^{M-1}X(W_M^r z^{(1/M)})V1(z)=1/M∑r=0M−1X(WMrz(1/M))
Y1(z)=H(z)V1(z)=1MH(z)∑r=0M−1X(WMrz1/M)Y_1 (z)=H(z) V_1 (z)=\frac1M H(z)\sum_{r=0}^{M-1}X(W_M^r z^{1/M})Y1(z)=H(z)V1(z)=M1H(z)∑r=0M−1X(WMrz1/M)
V2(z)=H(zD)X(z)其中H(zD)V_2 (z)=H(z^D )X(z) 其中 H(z^D )V2(z)=H(zD)X(z)其中H(zD)相当于对H(z)进行D倍内插
Y2(z)=1/M∑r=0M−1H(WMrz1M)MX(WMrz1M)Y_2 (z)= 1/M \sum_{r=0}^{M-1}H{(W_M^r z^{\frac1M}})^M X(W_M^r z^{\frac1M})Y2(z)=1/M∑r=0M−1H(WMrzM1)MX(WMrzM1)
因为WMrM=1W_M^{rM}=1WMrM=1,所以Y2(z)=1/M∑r=0M−1H(WMrz1M)=1MH[z]∑r=0M−1X(WMrz1/M)=Y1(z)Y_2 (z)= 1/M \sum_{r=0}^{M-1}H{(W_M^r z^{\frac1M}})= \frac1M H[z]\sum_{r=0}^{M-1}X(W_M^r z^{1/M} ) =Y_1 (z)Y2(z)=1/M∑r=0M−1H(WMrzM1)=M1H[z]∑r=0M−1X(WMrz1/M)=Y1(z)
1.6.2内插
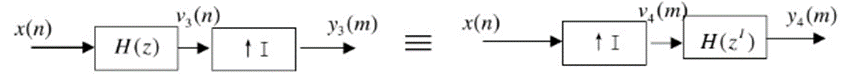
XI(z)=X(zI)X_I (z)=X(z^I)XI(z)=X(zI)
V3(z)=H(z)X(z)V_3 (z)=H(z)X(z)V3(z)=H(z)X(z)
Y3(z)=V3(zI)=H(zI)X(zI)Y_3 (z)=V_3 (z^I )= H(z^I) X(z^I)Y3(z)=V3(zI)=H(zI)X(zI)
V4(z)=X(zI)V_4 (z)=X(z^I)V4(z)=X(zI)
Y4(z)=H(zI)Y_4 (z)=H(z^I)Y4(z)=H(zI)
V4(z)=H(zI)V_4 (z)= H(z^I)V4(z)=H(zI)
X(zI)=Y3(z)X(z^I)= Y_3 (z)X(zI)=Y3(z)
1.7 信号的多相分解
输入x(n)经过长度为N的FIR滤波器滤波后输出为v(n),
v(n)=∑m=0N−1h(m)x(n−m)v(n)=\sum_{m=0}^{N-1}h(m)x(n-m)v(n)=∑m=0N−1h(m)x(n−m),对v(n)每隔M个点进行抽样一次,作为下抽样器的输出,因此在上式中只需要在n=kM(k=1,2,...)处计算v(n)n=kM(k=1,2,...)处计算v(n)n=kM(k=1,2,...)处计算v(n)的值即可。可以跳过其他中间的样值,使得计算复杂度节省为原来的1/M。假设系统下抽样率为M,对于序列h(n),有,
H(z)=∑n=0∞h(n)z−n=h(0)+h(M)z−M+h(2M)z−2M+...+h(1)z−1+h(M+1)z−(M+1)+h(2M+1)z−(2M+1)+....+h(2)z−2+h(M+2)z−(M+2)+h(2M+2)z−(2M+2)+....+h(M−1)z−(M−1)+h(2M−1)z−(2M−1)+h(3M−1)z−(3M−1)+..=z0[h(0)+h(M)z−M+h(2M)z−2M]+z−1[h(1)+h(M+1)z−M+h(2M+1)z−2M]+z−2[h(2)+h(M+2)z−M+h(2M+2)z−2M]+...+z−(M−1)[h(M−1)+h(M+M−1)z−M+h(2M+M−1)z−2M]+... \begin{aligned} H(z) &= \sum_{n=0}^∞ h(n) z^{-n} \\ &=h(0) + h(M)z^{-M}+ h(2M) z^{-2M}+...\\ &+ h(1) z^{-1} + h(M+1)z^{-(M+1)} + h(2M+1)z^{-(2M+1)} +....\\ &+h(2)z^{-2} + h(M+2)z^{-(M+2)} + h(2M+2)z^{-(2M+2)} +....\\ &+h(M-1)z^{-(M-1)} +h(2M-1)z^{-(2M-1)} +h(3M-1)z^{-(3M-1)}+..\\ &=z^0 [h(0)+h(M) z^{-M}+h(2M) z^{-2M}]\\ &+z^{-1} [h(1)+h(M+1)z^{-M}+h(2M+1)z^{-2M}]\\ &+z^{-2}[h(2)+h(M+2)z^{-M}+h(2M+2)z^{-2M}]+...\\ &+z^{-(M-1)} [h(M-1)+h(M+M-1)z^{-M}+h(2M+M-1)z^{-2M}]+... \end{aligned} H(z)=n=0∑∞h(n)z−n=h(0)+h(M)z−M+h(2M)z−2M+...+h(1)z−1+h(M+1)z−(M+1)+h(2M+1)z−(2M+1)+....+h(2)z−2+h(M+2)z−(M+2)+h(2M+2)z−(2M+2)+....+h(M−1)z−(M−1)+h(2M−1)z−(2M−1)+h(3M−1)z−(3M−1)+..=z0[h(0)+h(M)z−M+h(2M)z−2M]+z−1[h(1)+h(M+1)z−M+h(2M+1)z−2M]+z−2[h(2)+h(M+2)z−M+h(2M+2)z−2M]+...+z−(M−1)[h(M−1)+h(M+M−1)z−M+h(2M+M−1)z−2M]+...
H(z)=∑l=0M−1z−l∑n=0+∞h(nM+l)z−nMH(z)=\sum_{l=0}^{M-1}z^{-l} \sum_{n=0}^{+∞}h(nM+l)z^{-nM}H(z)=l=0∑M−1z−ln=0∑+∞h(nM+l)z−nM
令El(z)=∑n=0+∞h(nM+l)z−nME_l (z)=\sum_{n=0}^{+∞}h(nM+l)z^{-nM}El(z)=∑n=0+∞h(nM+l)z−nM,所以H(z)=∑l=0M−1El(z)z−lH(z)=\sum_{l=0}^{M-1}E_l (z) z^{-l}H(z)=∑l=0M−1El(z)z−l
1.8 多相滤波器
解决的是多速率问题,通过降采样、插值来改变信号的输出速率(主要利用Nyquist采样定理,保证不混叠),从而降低数据率,多相滤波器为这类操作提供了实现框架。在满足采样定理的前提下,内插/抽取并配合滤波器使用(防止混叠),可以改变数据的速率。
多相滤波的结构也多用在信道化中(即构建滤波器组),固化系数借助硬件实现快速运算。
H(z)=∑n=0∞h(n)z−n=∑l=−∞+∞h(Dl)z−Dl+∑l=−∞+∞h(Dl+1)z−(Dl+1)+⋯+∑l=−∞+∞h(Dl+D−1)z−(Dl+D−1)=∑l=−∞+∞h(Dl)z−Dl+z−1∑l=−∞+∞h(Dl+1)z−Dl+⋯+z−(D−1)∑l=−∞+∞h(Dl+D−1)z−Dl \begin{aligned} H(z) &= \sum_{n=0}^∞ h(n) z^{-n} \\ &=\sum_{l=-∞}^{+∞}h(Dl) z^{-Dl}+\sum_{l=-∞}^{+∞}h(Dl+1) z^{-(Dl+1) }+⋯\\ &+\sum_{l=-∞}^{+∞}h(Dl+D-1) z^{-(Dl+D-1)} \\ &=\sum_{l=-∞}^{+∞}h(Dl) z^{-Dl}+z^{-1} \sum_{l=-∞}^{+∞}h(Dl+1) z^{-Dl}+⋯ +z^{-(D-1)} \sum_{l=-∞}^{+∞}h(Dl+D-1) z^{-Dl} \end{aligned} H(z)=n=0∑∞h(n)z−n=l=−∞∑+∞h(Dl)z−Dl+l=−∞∑+∞h(Dl+1)z−(Dl+1)+⋯+l=−∞∑+∞h(Dl+D−1)z−(Dl+D−1)=l=−∞∑+∞h(Dl)z−Dl+z−1l=−∞∑+∞h(Dl+1)z−Dl+⋯+z−(D−1)l=−∞∑+∞h(Dl+D−1)z−Dl
Ej(z)=∑l=−∞+∞h(Dl+j)z−l,j=0,1,...D−1ej(n)=h(Dl+j),则H(z)=∑j=0D−1z−j∑l=−∞+∞Ej(zD) \begin{aligned} E_j (z)&=\sum_{l=-∞}^{+∞}h(Dl+j) z^{-l}, j=0,1,...D-1\\ e_j (n)&=h(Dl+j),\\ 则H(z)=\sum_{j=0}^{D-1}z^{-j} \sum_{l=-∞}^{+∞}E_j (z^D) \end{aligned} Ej(z)ej(n)则H(z)=j=0∑D−1z−jl=−∞∑+∞Ej(zD)=l=−∞∑+∞h(Dl+j)z−l,j=0,1,...D−1=h(Dl+j),
H(z)=∑j=0D−1z−j∑l=−∞+∞Ej(zD)H(z)=∑_{j=0}^{D-1}z^{-j} \sum_{l=-∞}^{+∞}E_j (z^D)H(z)=j=0∑D−1z−jl=−∞∑+∞Ej(zD)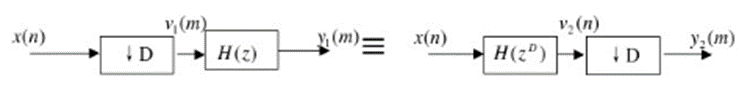


H(z)=∑n=0∞h(n)z−n=∑l=−∞+∞h(Il)z−Il+∑l=−∞+∞h(Il+1)z−(Il+1)+⋯+∑l=−∞+∞h(Il+I−1)z−(Il+I−1)=∑j=0l−1∑l=−∞+∞h(Il+j)z−(Il+j)=∑j=0l−1z−j∑l=−∞+∞h(Il+j)z−Il=∑j=0l−1Ej(zI)z−j=∑j=0l−1EI−1−j(zI)z−(I−1−j) \begin{aligned} H(z)&= \sum_{n=0}^∞h(n) z^{-n}\\ &=\sum_{l=-∞}^{+∞}h(Il) z^{-Il}+\sum_{l=-∞}^{+∞}h(Il+1) z^{-(Il+1) }+⋯+\sum_{l=-∞}^{+∞}h(Il+I-1)z^{-(Il+I-1)}\\ &=\sum_{j=0}^{l-1}\sum_{l=-∞}^{+∞}h(Il+j) z^{-(Il+j)}=\sum_{j=0}^{l-1}z^{-j}\sum_{l=-∞}^{+∞}h(Il+j) z^{-Il}\\ &=\sum_{j=0}^{l-1}E_j (z^I )z^{-j}=\sum_{j=0}^{l-1}E_{I-1-j} (z^I ) z^{-(I-1-j)}\\ \end{aligned} H(z)=n=0∑∞h(n)z−n=l=−∞∑+∞h(Il)z−Il+l=−∞∑+∞h(Il+1)z−(Il+1)+⋯+l=−∞∑+∞h(Il+I−1)z−(Il+I−1)=j=0∑l−1l=−∞∑+∞h(Il+j)z−(Il+j)=j=0∑l−1z−jl=−∞∑+∞h(Il+j)z−Il=j=0∑l−1Ej(zI)z−j=j=0∑l−1EI−1−j(zI)z−(I−1−j)
其中Ej(zI)=∑l=−∞+∞h(Il+j)z−Il,令j=I−1−j′,定义Rj(z)=E(I−1−j)(z)其中E_j (z^I )=\sum_{l=-∞}^{+∞}h(Il+j)z^{-Il},令j=I-1-j',定义R_j (z)=E_{(I-1-j)} (z)其中Ej(zI)=∑l=−∞+∞h(Il+j)z−Il,令j=I−1−j′,定义Rj(z)=E(I−1−j)(z)
H(z)=∑j=0I−1z−(I−1−j)Rj(zI)H(z)= \sum_{j=0}^{I-1}z^{-(I-1-j)} R_j (z^I )H(z)=∑j=0I−1z−(I−1−j)Rj(zI)
H(z)=∑j=0I−1z−(I−1−j)Rj(zI)H(z)= \sum_{j=0}^{I-1}z^{-(I-1-j)} R_j (z^I )H(z)=j=0∑I−1z−(I−1−j)Rj(zI)


1.9 内插后滤波

输入信号Xk(m)X_k (m)Xk(m)先经过M倍内插后,得到:h(r)=∑m=−∞+∞Xk(m)δ(r−mM)h(r)=\sum_{m=-∞}^{+∞}X_k (m)δ(r-mM)h(r)=∑m=−∞+∞Xk(m)δ(r−mM)
再经过f(n)滤波得到:
y(n)=∑r=−∞+∞h(r)f(n−r)=∑r=−∞+∞∑m=−∞+∞Xk(m)δ(r−mM)f(n−r)=∑m=−∞+∞Xk(m)∑r=−∞+∞f(n−r)δ(r−mM)=∑m=−∞+∞Xk(m)f(n−mM) \begin{aligned} y(n)=\sum_{r=-∞}^{+∞}h(r)f(n-r)&= \sum_{r=-∞}^{+∞}\sum_{m=-∞}^{+∞}X_k (m)δ(r-mM) f(n-r) \\ &=\sum_{m=-∞}^{+∞}X_k (m)\sum_{r=-∞}^{+∞}f(n-r) δ(r-mM)\\ &=\sum_{m=-∞}^{+∞}X_k (m)f(n-mM) \end{aligned}y(n)=r=−∞∑+∞h(r)f(n−r)=r=−∞∑+∞m=−∞∑+∞Xk(m)δ(r−mM)f(n−r)=m=−∞∑+∞Xk(m)r=−∞∑+∞f(n−r)δ(r−mM)=m=−∞∑+∞Xk(m)f(n−mM)
1.10 verilog多相分解实现
verilog实现四阶多相抽取滤波器,实现2倍下采样,其多相传递函数为:
G(z)=(124+57z−2)/256+z−1(214−33z−2)g(n)=[124/256=h(n),214=h(n−1),57/256=h(n−2),33=h(n−3)]G(z)=(124+57z^{-2})/256+z^{-1} (214-33z^{-2})\\ g(n)=[124/256=h(n),214=h(n-1),57/256=h(n-2),33=h(n-3)]G(z)=(124+57z−2)/256+z−1(214−33z−2)g(n)=[124/256=h(n),214=h(n−1),57/256=h(n−2),33=h(n−3)]
module polyfilter (clk, clk2, reset, x_in, y_out);
parameter even=0, odd=1;
input clk; // 输入信号的速率
input clk2; // 输入信号的速率的一半
input reset;
input [7:0] x_in; // 输入信号
output [8:0] y_out; // 输出信号
// 各种中间寄存器,包括系数以及乘法器的输入参数
reg [16:0] m0, m1, m2, m3, r0, r1, r2, r3;
reg [16:0] x33, x99, x107;
reg [16:0] y;
reg [7:0] x_odd, x_even, x_wait; //多相分解的开的奇、偶信号
wire [16:0] x_odd_sxt, x_even_sxt;
reg state;
always @(posedge clk) begin // 按照奇、偶分开
if(!reset) begin //初始化寄存器
state <= even;
x_even <= 0;
x_odd <= 0;
end
else begin
case (state)
even : begin
x_even <= x_in;
x_odd <= x_wait;
state <= odd;
end
odd : begin
x_wait <= x_in;
state <= even;
end
endcase
end
end
//对奇偶项的数据进行符号扩展
assign x_odd_sxt = {{9{x_odd[7]}},x_odd};
assign x_even_sxt = {{9{x_even[7]}},x_even};
always @(posedge clk) begin // 完成滤波
if(!reset) begin
x33 = 0; //初始化寄存器
x99 = 0;
x107 = 0;
m0 = 0;
m1 = 0;
m2 = 0;
m3 = 0;
end
else begin
x33 = (x_odd_sxt << 5) + x_odd_sxt; //33*x_odd_sxt
x99 = (x33 << 1) + x33; //99* x_odd_sxt
x107 = x99 + (x_odd_sxt << 3); //107* x_odd_sxt
// 计算滤波输出
m0 = (x_even_sxt << 7) - (x_even_sxt << 2); // m0 = 124,124*x_even_sxt
m1 = x107 << 1; // m1 = 214,214* x_odd_sxt
m2 = (x_even_sxt << 6) - (x_even_sxt << 3) + x_even_sxt;// m2 =57
//57* x_even_sxt
m3 = x33; // m3 = -33,33*x_odd_sxt
end
end
always @(negedge clk2) begin //参考寄存器
if(!reset) begin
r0 <= 0;
r2 <= 0;
r1 <= 0;
r3 <= 0;
end
else begin
//计算滤波器G0
r0 <= r2 + m0; // g0 = 128
r2 <= m2; // g2 = 57
//计算滤波器 G1
r1 <= -r3 + m1; // g1 = 214
r3 <= m3; // g3 = -33
// 多相输出信号
y <= r0 + r1;
end
end
assign y_out = y[16:8]; //完成输出信号赋值
endmodule
1.11有理数的采样速率转换
在进行D/A转换时,如果数字信号的速率和奈奎斯特速率相同,那么和整数倍抽取器的抗混叠滤波器相同,为正确恢复原始信号,必须有一个非常尖锐的截止频率,需要一个高精度的高阶模拟重构滤波器.
单独的抽取器和内插器只能实现整数倍的采样率转换,可以采用先内插后抽取的方法直接实现抽样率比值为有理数的变换,根据整数倍抽取和内插的原理,速率转换过程中均需要使用低通滤波器为抗混叠滤波器。因此设计一个截止频率为二者带宽最小值的低通滤波器即可。
输入信号先经过R1倍内插,再通过低通滤波器滤波(具有抗混叠滤波和消除镜像滤波作用)后,在经过R2倍抽取后输出即可实现R1/R2倍的有理采样速率转换。
采样率的分数倍转换假设输入输出信号采样率的转换因子为R=I/D可以通过将D抽取与I插值结合来实现为了保证不丢失信息,分数倍采样率转换应先插值后抽取.
∣H(ejw)∣={D,∣w∣<min[π/I,π/D]0,其他(5) |H(e^{jw})|= \begin{cases} D,\quad |w|<min[π/I,π/D]\\ 0, \quad 其他 \end{cases} \tag{5} ∣H(ejw)∣={D,∣w∣<min[π/I,π/D]0,其他(5)
1.12 抗混叠滤波器要求
- 滤波器在有用信号频段内纹波系数满足要求,
- 抽取或者内插处理后,在有用信号频段内频谱不发生混叠。
- 滤波器占用硬件资源少,且运算速度快。
- 一般说来,根据数字滤波器的设计原理,只要有效增加数字滤波器的阶数,总可以设计出满足指标要求的抗混叠滤波器。
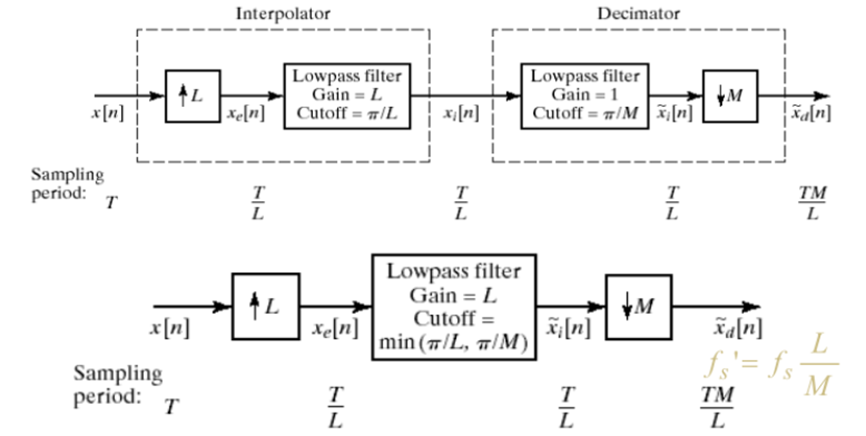
增采样之后,只是填充零,但会在幅度上引起L的变化。根据帕斯瓦尔定理,能量是不变的,因为0是没有能量的。采样导致频率周期性,低通滤波器,把频域上中间那段取出来了,能量降低为1/L*L ,为了恢复x(0),低通滤波器增益为L。
下面是MATLAB的仿真说明:
F = [0 0.250 0.500 0.7500 1];
A = [1.0000 0.5000 0 0 0];
Order = 511;
B = fir2(Order,F,A);
[Hx,W] = freqz(B,1,8192,'whole');
Hx = [Hx(4098:end) ; Hx(1:4097)];
omega = -pi+(2*pi/8192):(2*pi)/8192:pi;
plot(omega,abs(Hx))
xlim([-pi pi])
xlabel('Radians/Sample')
ylabel('Magnitude')
y = interp(B,2);
[Hy,W] = freqz(y,1,8192,'whole');
Hy = [Hy(4098:end) ; Hy(1:4097)];
hold on
plot(omega,abs(Hy),'r','linewidth',2)
legend('Original Signal','Upsampled Signal')
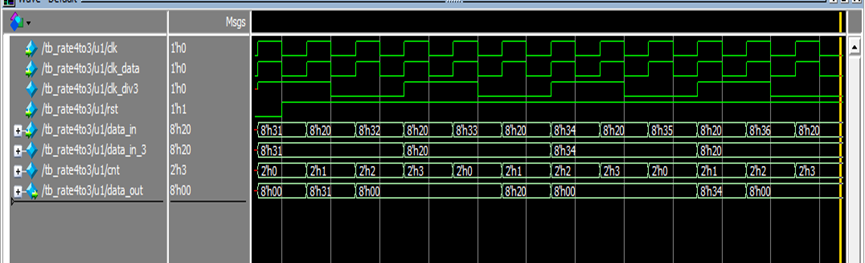
1.13 Verilog 4/3采样速率转换
.verilog实现
利用Verilog实现输入数据的4/3采样速率转换
module rate4to3(
input clk,
input clk_data, //输入数据的时钟
input rst,
input [7:0] data_in,
output reg [7:0] data_out
);
reg [7:0] data_in_3;
reg [1:0] cnt;
// 3 times decimal,3分频后的时钟
wire clk_div3;
clkdiv3 clkdiv3(
.clk(clk_data),
.rst(rst),
.div3(clk_div3)
);
always @(posedge clk_div3)
data_in_3 <= data_in; //3倍抽取
always @(posedge clk) begin //3倍抽取后的数据再4倍内插
if(!rst) begin
cnt <= 2'b00;
data_out<= 0;
end
else begin
cnt <= cnt +1;
if(cnt <= 2'b00)
data_out<= data_in_3;
else
data_out <= 0;
end
end
endmodule
2.CIC滤波器
一般用于数字下变频(DDC)和数字上变频(UDC),CIC滤波器结构简单,没有乘法器,只有加法器、积分器和寄存器,适合于工作在高采样率条件下,是一种基于零点相消的FIR滤波器。
- 单级CIC滤波器
CIC滤波器的冲激响应为:
h(n)={1,0≤n≤M−10,其他(6) h(n)= \begin{cases} 1,\quad 0≤n≤M-1\\ 0, \quad 其他 \end{cases} \tag{6} h(n)={1,0≤n≤M−10,其他(6)
式中,M为滤波器的长度,从滤波器的冲激响应来看,CIC滤波器是一种具有线性相位的特殊FIR滤波器。
H(z)=∑n=0M−1h(n)z−n=∑n=0M−1z−nH(z)=\sum_{n=0}^{M-1}h(n)z^{-n} =\sum_{n=0}^{M-1}z^{-n}H(z)=∑n=0M−1h(n)z−n=∑n=0M−1z−n(无反馈结构的FIR滤波器);
H(z)=∑n=0M−1z−n=1−z−M1−z−1H(z)=\sum_{n=0}^{M-1}z^{-n} =\frac{1-z^{-M}}{1-z^{-1}}H(z)=∑n=0M−1z−n=1−z−11−z−M (具有反馈结构的IIR滤波器);
对h(n)进行离散时间傅里叶变换,得到其频谱特性:
H(ejw)=∑n=0M−1h(n)e−jwn=∑n=0M−1e−jwnH(e^jw)= \sum_{n=0}^{M-1}h(n)e^{-jwn}=\sum_{n=0}^{M-1}e^{-jwn}H(ejw)=∑n=0M−1h(n)e−jwn=∑n=0M−1e−jwn,∣H(ejw)∣=∣(sin(wM/2))/(sin(w/2))∣|H(e^{jw})|=|(sin(wM/2))/(sin(w/2))|∣H(ejw)∣=∣(sin(wM/2))/(sin(w/2))∣
主瓣区间WM2=π,W=2π/M,其中[0,2π/M]\frac{WM}2=π,W=2π/M,其中[0,2π/M]2WM=π,W=2π/M,其中[0,2π/M]为主瓣,其他的区间为旁瓣。
当W=0时,∣H(ejw)∣=M|H(e^{jw})|=M∣H(ejw)∣=M,随着频率增大,第一旁瓣电平不断减小。
CIC滤波器,级数(Number Of Sections)设置为4,表示四级CIC滤波器。这里设置为对25MHz的Fs进行5倍抽取(decimation factor)。
2.1 单级CIC滤波器频谱
单级CIC抽取滤波器,级数N=1,积分部分的积分器是单极点的IIR滤波器,并且反馈系数为1,状态方程为:y(n)=y(n-1)+x(n),积分器的传输函数为HI(z)=1/(1−z−1)H_I (z)=1/(1-z^{-1} )HI(z)=1/(1−z−1),梳状器是一个对称的FIR滤波器,其状态方程为:y(n)=x(n)−x(n−DM)y(n)=x(n)-x(n-DM)y(n)=x(n)−x(n−DM),D为设计参数,为微分延迟,其传输函数为:Hc(z)=1−z−DMH_c (z)=1-z^{-DM}Hc(z)=1−z−DM,则单级CIC滤波器的传递函数为:
H(z)=(1−z−DM)/(1−z−1)H(z)=(1-z^{-DM})/(1-z^{-1} )H(z)=(1−z−DM)/(1−z−1),N级CIC滤波器的表示函数为:H(z)=(1−z−DM1−z−1)NH(z)=(\frac{1-z^{-DM}}{1-z^{-1} })^NH(z)=(1−z−11−z−DM)N
Noble恒等式:
对于多级系统包括线性系统、内插器、抽取器时,可以在处理信号的流程中重新排列这三个部分的处理顺序,以便可以以更简便的方式实现。
如果线性系统F(z^M)后面紧跟着M倍抽取器,则下式成立:F(zM)(↓M)=(↓M)F(z)F(z^M)(↓M)= (↓M)F(z)F(zM)(↓M)=(↓M)F(z),这表明调换线性系统的抽取系统的处理顺序,即首先进行抽取,然后进行线性滤波,就可以将线性滤波器的长度降低M倍,即滤波器的抽头数为原来的1/M,同理如果在线性系统前有L倍内插器,(↑L)F(zL)=F(z)(↑L)(↑L)F(z^L)= F(z) (↑L)(↑L)F(zL)=F(z)(↑L),在插值时,将线性系统放置在插值器之前,就可以得到阶数降低L倍的插值器。
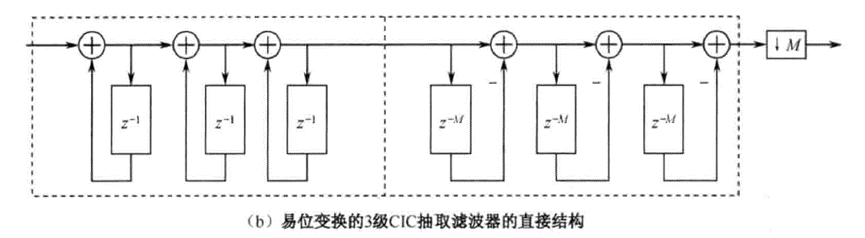
3级5阶CIC滤波器的结构特性,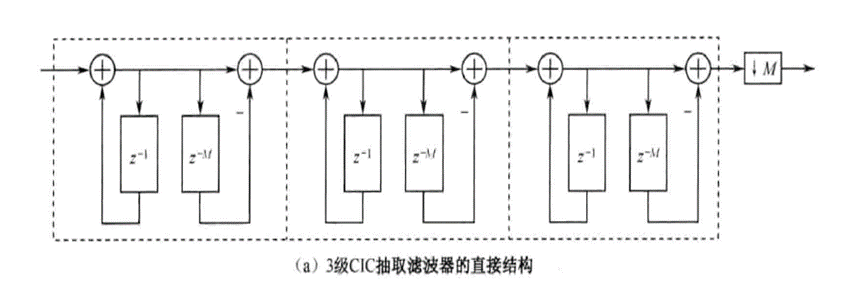
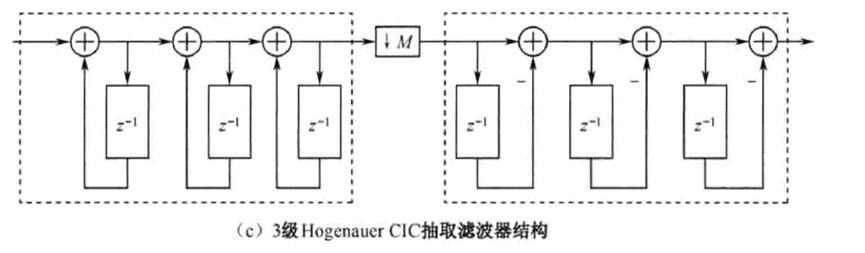
%用Matlab仿真不同长度的单级CIC滤波器的频谱特性。
M=2; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s))); %求取滤波器频谱特性
Spec2=Spec-max(Spec);
f=0:length(Spec)-1;
f=2*f/(length(Spec)-1); %对频率轴进行归一化处理
%归一化频率,数值1相当于数据速率的一半。
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s))); %求取滤波器频谱特性
Spec5=Spec-max(Spec);
M=7; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s))); %求取滤波器频谱特性
Spec7=Spec-max(Spec);
M=8; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s))); %求取滤波器频谱特性
Spec8=Spec-max(Spec);
% plot(f,Spec2,f,Spec5,f,Spec7,f,Spec8);axis([0 1 -50 0]);grid;
% xlabel('归一化频率');ylabel('幅度(dB)');
% legend('M=2','M=5','M=7','M=8');
% grid;
plot(f,Spec2,'-',f,Spec5,'.',f,Spec8,'--');axis([0 1 -50 0]);
xlabel('归一化频率');ylabel('幅度(dB)');
legend('M=2','M=5','M=8');
grid;
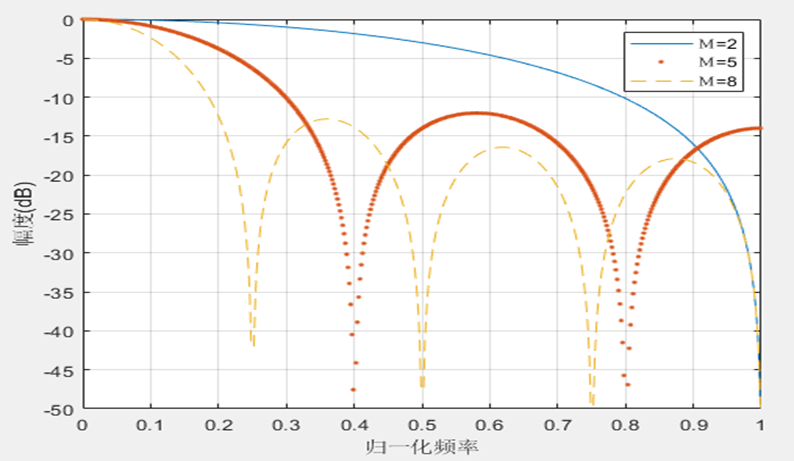
横坐标轴归一化频率,数值1相当于数据速率的一半。CIC滤波器的频谱特性很像一把梳子,这也是CIC滤波器被称为梳状滤波器的
原因,随着滤波器的长度M远大于1时,第一旁瓣电平相对于主瓣电平的差值几乎是固定的13.46dB。显然这么小的阻带衰减远不能满足较高的滤波器要求,可以对滤波器级联,每增加一级滤波器,旁瓣衰减增加13.46dB,例如利用5级滤波器级联,则旁瓣电平衰减变为67.3dB,增加滤波器的级联的数目虽然可以解决旁瓣电平衰减小的问题,但会带来其他不利影响。假设有N级级联,则阻带衰减为单级衰减的N倍,即13.46*N.
2倍抽取的matlab实现
r = 2; % 抽取因子
fs = 44.1e3; %原始的采样率 44.1kHz.
n = 0:10239; % 10240个采样点
x = sin(2*pi*1e3/fs*n); %原始信号
y=x(1:r:length(x));
x = double(x);
y = y/max(abs(y));
stem(n(2:45)/fs,x(2:45)); hold on;
stem(n(1:22)/(fs/r),y(1:22),'r','filled');
xlabel('时间(sec)');ylabel('信号值');
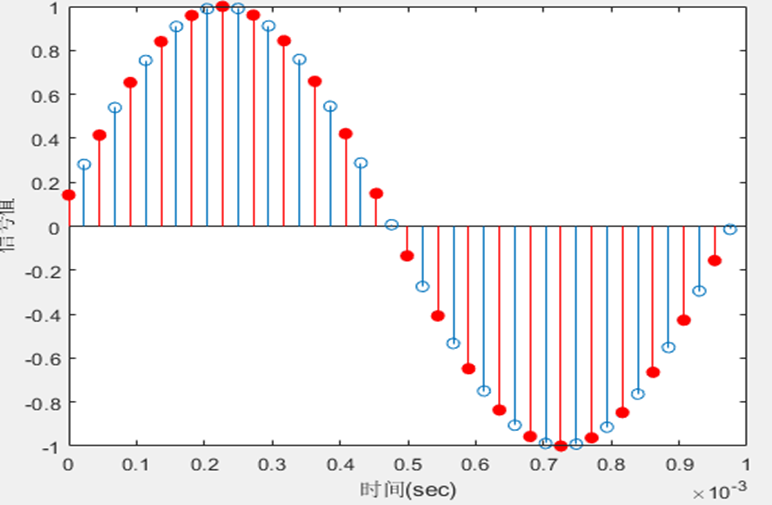
2倍内插的matlab实现
R= 2; % 抽取因子
fs = 44.1e3; %原始的采样率 44.1kHz.
n = 0:10239; % 10240个采样点
x = sin(2pi1e3/fsn); %原始信号
y=zeros(1,Rlength(x));
y(1:R:length(y))=x;
x = double(x);
y = y/max(abs(y));
stem(n(1:41)/fs,x(1:41),‘filled’);
hold on;
stem(n(2:82)/(fs*R),y(2:82),‘r’);
xlabel(‘时间(sec)’);ylabel(‘信号值’);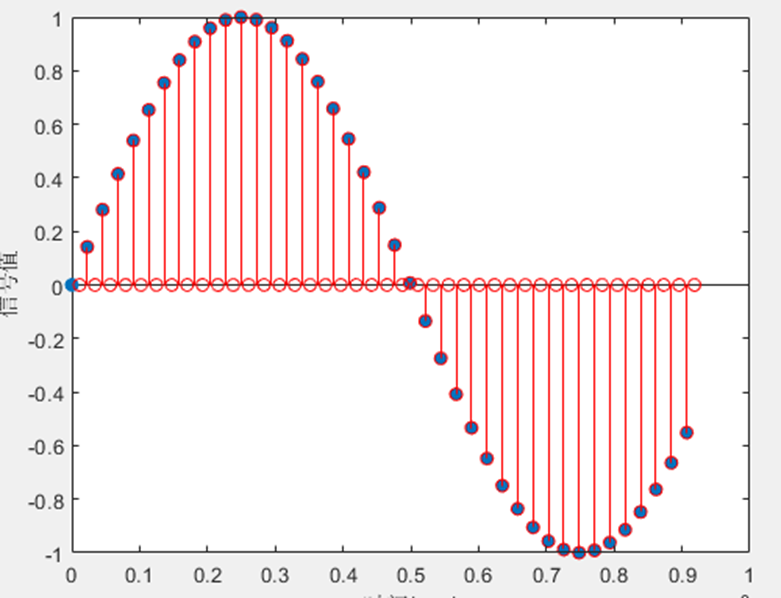
2.2.单级CIC滤波器的Verilog实现
Verilog设计抽取倍数为5,5阶CIC滤波器作为抗混叠滤波器。
2.3多级CIC滤波器
1.级数固定,每级长度不同
用matlab仿真不同长度的5级CIC滤波器的频谱特性,为了进一步降低CIC滤波器的旁瓣电平,可以采用多级CIC滤波器级联的方法,利用
matlab仿真不同长度的5级CIC滤波器的频谱特性代码如下(MultCIC .M):
%E6_4_MultCIC.M
%例6-4:
%用Matlab仿真不同长度的5级CIC滤波器的频谱特性。
M=2; %滤波器长度
b=ones(1,M); %CIC滤波器的h(n)
delta=[1,zeros(1,1023)]; % delta函数 ,δ(n)
s1=filter(b,1,delta); %求取输入为delta(n)的第一级滤波器冲激响应
s2=filter(b,1,s1);%求取输入为第一级输出s1的第二级滤波器冲激响应
s3=filter(b,1,s2);%求取输入为第二级输出s2的第三级滤波器冲激响应
s4=filter(b,1,s3);%求取输入为第三级输出s3的第四级滤波器冲激响应
s=filter(b,1,s4); %求取输入为第四级输出s4的第五级滤波器冲激响应
Spec=20*log10(abs(fft(s))); %求取滤波器频谱特性
Spec2=Spec-max(Spec);
f=0:length(Spec)-1;
f=2*f/(length(Spec)-1); %对频率轴进行归一化处理
%横坐标轴归一化频率,数值1相当于数据速率的一半
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s))); %求取滤波器频谱特性
Spec5=Spec-max(Spec);
M=7; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s))); %求取滤波器频谱特性
Spec7=Spec-max(Spec);
M=8; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s))); %求取滤波器频谱特性
Spec8=Spec-max(Spec);
% plot(f,Spec2,f,Spec5,f,Spec7,f,Spec8);axis([0 1 -50 0]);grid;
% xlabel('归一化频率');ylabel('幅度(dB)');
% legend('M=2','M=5','M=7','M=8');
% grid;
plot(f,Spec2,'-',f,Spec5,'.',f,Spec8,'--');axis([0 1 -200 0]);
xlabel('归一化频率');ylabel('幅度(dB)');
legend('M=2','M=5','M=8');
grid;
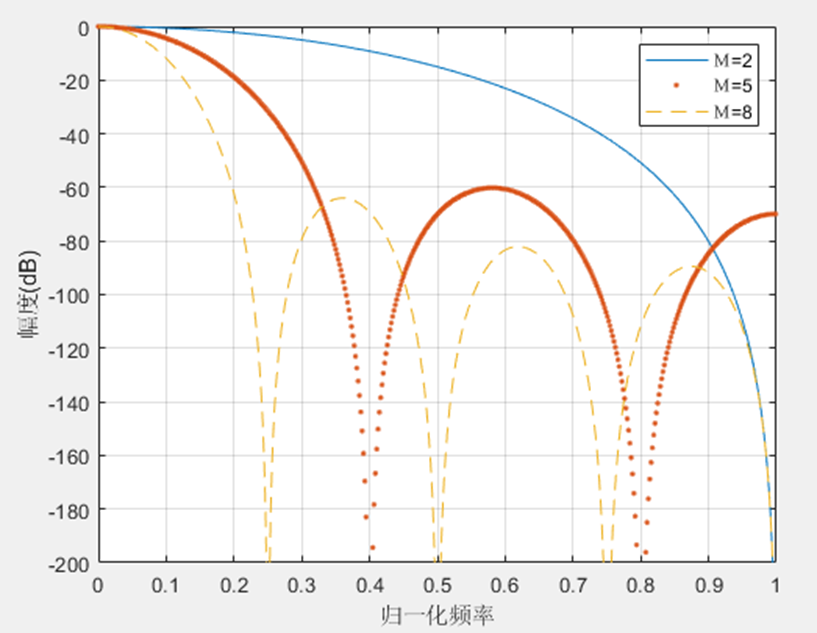
不同长度的5级CIC滤波器的频谱特性
从图中可以看出,相对于单级的CIC滤波器,多级级联CIC滤波器的旁瓣电平的衰减达到67.3dB,但同时也可以看到,多级CIC滤波器的主瓣电平值下降也要比单级快得多,在相同的通带范围内,多级CIC滤波器的通带衰减也明显增加。
2.4 长度固定,改变级联数
用matlab仿真不同级联数的5阶CIC滤波器的频谱特性,
分析代码如下:
%E6_5_CompareCIC.M
%例6-5:
%用Matlab仿真长度为5的不同级联数CIC滤波器的频谱特性。
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取第一级输出滤波器冲激响应
s2=filter(b,1,s1); %求取第二级输出滤波器冲激响应
s3=filter(b,1,s2); %求取第三级输出滤波器冲激响应
s4=filter(b,1,s3); %求取第四级输出滤波器冲激响应
s5=filter(b,1,s4); %求取第五级输出滤波器冲激响应
Spec1=20*log10(abs(fft(s1))); %求取滤波器频谱特性
Spec1=Spec1-max(Spec1);
Spec2=20*log10(abs(fft(s2))); %求取滤波器频谱特性
Spec2=Spec2-max(Spec2);
Spec3=20*log10(abs(fft(s3))); %求取滤波器频谱特性
Spec3=Spec3-max(Spec3);
Spec4=20*log10(abs(fft(s4))); %求取滤波器频谱特性
Spec4=Spec4-max(Spec4);
Spec5=20*log10(abs(fft(s5))); %求取滤波器频谱特性
Spec5=Spec5-max(Spec5);
f=0:length(Spec)-1;
f=2*f/(length(Spec)-1); %对频率轴进行归一化处理
plot(f,Spec1,'-',f,Spec2,'.',f,Spec3,'--',f,Spec5,'-.');axis([0 0.2 -25 0]);
xlabel('归一化频率');ylabel('幅度(dB)');
legend('D=1','D=2','D=3','D=5');
grid;
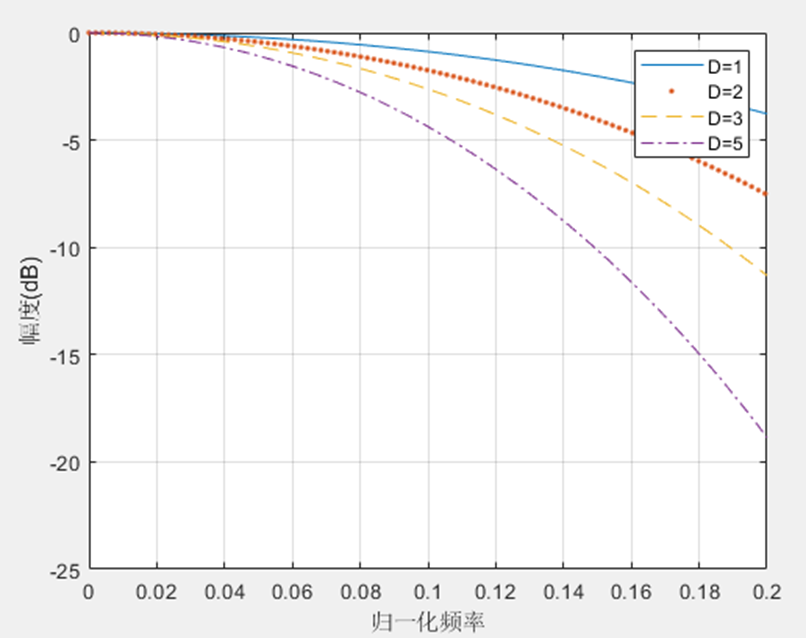
长度为5的不同级联数CIC滤波器的频谱特性
从图中可以看出,分析对于归一化通带频率为0.2的不同级联数的通带衰减,单级滤波器的通带衰减为3.8dB,两级滤波器的通带衰减为7.5dB,5级滤波器则已达到18.9dB。所以对于给定的通带衰减要求,多级滤波器由于通带衰减要大得多,所以对于给定的通带衰减,多级滤波器的通带范围要小于单级滤波器的通带范围。
2.5 CIC滤波器应用条件
抗混叠滤波器最重要的指标有通带容限δpδ_pδp或通带衰减αpα_pαp,阻带容限δsδ_sδs或者阻带衰减αsα_sαs,通带截止频率fp以及阻带截止频率fs。设计的滤波器是否满足要求,也使用上面的指标衡量的。所以讨论CIC滤波器的应用条件也是在即是在给定过渡带条件下的通带容限和阻带容限的大小。
αp=20lg(1+δp)/(1−δp),αs=20lgδsα_p=20lg(1+δ_p)/(1-δ_p ), α_s=20lgδ_sαp=20lg(1+δp)/(1−δp),αs=20lgδs.
CIC滤波器的频谱形状相似,在给定过渡带的条件下,通带容限与阻带容限的取值只与滤波器的阶数(长度)和级联数有关。对于单级CIC滤波器来说,其对应关系为:
δp=16(πMfpF0)2,δs=fsM/F0δ_p=\frac16 (\frac{πMfp}{F_0} )^2, δ_s=f_sM/F_0δp=61(F0πMfp)2,δs=fsM/F0.
对于多级滤波器(设级联数为n)来说,各级滤波器的误差容限与系统总误差容限的关系为:
δp=δp1+δp2+⋯+δpn,δs=δs1δs2…..δsnδ_p=δ_{p1}+δ_{p2}+⋯+δ_{pn}, δ_s=δ_{s1} δ_{s2}…..δ_{sn}δp=δp1+δp2+⋯+δpn,δs=δs1δs2…..δsn
从上式也看出,多级CIC滤波器与单级相比,通带容限增加,(通带衰减增加)的同时,阻带容限减小(阻带衰减增加)。
4.通带与误差容限的关系
用matlab仿真不同长度的5级CIC滤波器的频带与误差容限的关系,代码如下:
%E6_6_ErrorCIC.M
%采用Matlab仿真的方法来绘出不同长度的5级CIC滤波器的通带、阻带与误差容限之间的关系。
D=5; %CIC滤波器级联数
F0=2; %归一化频率,采样频率的一半等于1
M=5; %CIC滤波器阶数
fp=0:0.001:1/M/8; %通带截止归一化频率
Ep=(1/6)*(pi*M*fp./F0).^2;
Ep=Ep*D;
Ap5=20*log10((1+Ep)./(1-Ep));
fs=0:0.001:1/M; %阻带截止归一化频率
Es=fs*M/F0;
As=20*log10(Es);
As5=As*D;
M=4; %CIC滤波器阶数
% fp=0:0.01:1/M; %通带截止归一化频率
Ep=(1/6)*(pi*M*fp./F0).^2;
Ep=Ep*D;
Ap4=20*log10((1+Ep)./(1-Ep));
Es=fs*M/F0;
As=20*log10(Es);
As4=As*D;
M=3; %CIC滤波器阶数
% fp=0:0.01:1/M; %通带截止归一化频率
Ep=(1/6)*(pi*M*fp./F0).^2;
Ep=Ep*M;
Ap3=20*log10((1+Ep)./(1-Ep));
Es=fs*M/F0;
As=20*log10(Es);
As3=As*D;
M=2; %CIC滤波器阶数
% fp=0:0.01:1/M; %通带截止归一化频率
Ep=(1/6)*(pi*M*fp./F0).^2;
Ep=Ep*M;
Ap2=20*log10((1+Ep)./(1-Ep));
Es=fs*M/F0;
As=20*log10(Es);
As2=As*D;
subplot(211);
plot(fp,Ap2,fp,Ap3,fp,Ap4,fp,Ap5);
xlabel('归一化频率');ylabel('通带衰减');
legend('M=2','M=3','M=4','M=5');
grid;
subplot(212);
plot(fs,As2,fs,As3,fs,As4,fs,As5);axis([0.02 0.2 -200 0]);
xlabel('归一化频率');ylabel('阻带衰减');
legend('M=2','M=3','M=4','M=5');
grid;
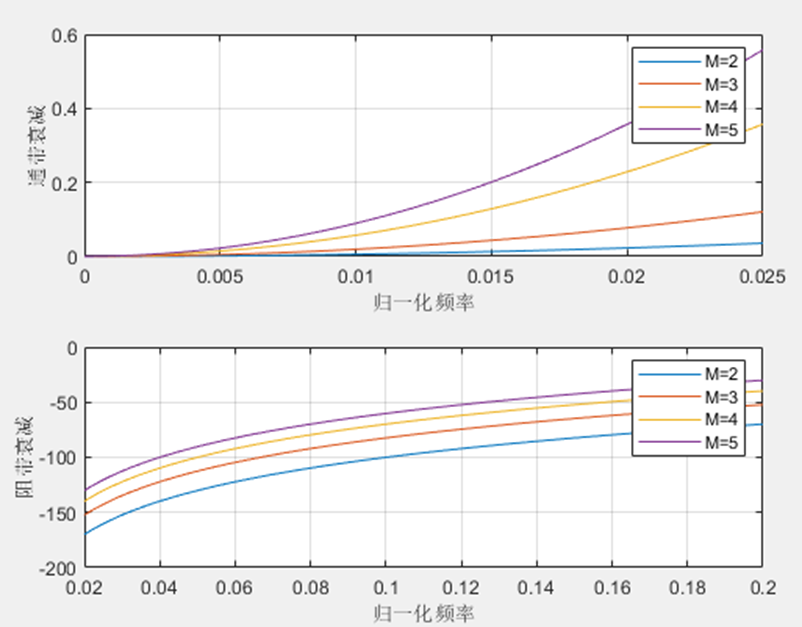
3.多阶CIC滤波器
h(n)=1;0≤n≤M-1;
h(n)=0;其他
式中,M为滤波器的长度,从滤波器的冲激响应来看,CIC滤波器
是一种具有线性相位的特殊FIR滤波器。
H(z)=∑n=0M−1h(n)z−n=∑n=0M−1z−nH(z)=\sum_{n=0}^{M-1}h(n)z^{-n} =\sum_{n=0}^{M-1}z^{-n}H(z)=∑n=0M−1h(n)z−n=∑n=0M−1z−n(无反馈结构的FIR滤波器);
H(z)=∑n=0M−1z−n=1−z−M1−z−1H(z)=\sum_{n=0}^{M-1}z^{-n} =\frac{1-z^{-M}}{1-z^{-1}}H(z)=∑n=0M−1z−n=1−z−11−z−M (具有反馈结构的IIR滤波器);
v(n)=x(n)+v(n-1) (积分模块),y(n)=v(n)-v(n-M)(梳状滤波模块)
多级CIC滤波器可以直接由多个单级CIC滤波器级联得到,但根据Noble恒等式(“先进行抽取或者插值,再进行线性滤波”与“先进行线性滤波,再进行抽取或者插值”这两者是可以等价的).
等效为:v(n)=x(n)+v(n−1)(积分模块,b=1,a=[1,−1]),M倍抽取,y(n)=v(n)−v(n−1)v(n)=x(n)+v(n-1) (积分模块,b=1,a=[1,-1]),\\ M倍抽取,y(n)=v(n)-v(n-1)v(n)=x(n)+v(n−1)(积分模块,b=1,a=[1,−1]),M倍抽取,y(n)=v(n)−v(n−1)(梳状滤波模块)
a0y(n)+a1y(n−1)+....+aMy(n−M)=b0x(n)+b1x(n−1)+b2x(n−2)+....+bNx(n−N)a_0y(n)+a_1y(n-1)+....+a_My(n-M)=b_0x(n)+b_1x(n-1)+b_2x(n-2)+....+b_Nx(n-N)a0y(n)+a1y(n−1)+....+aMy(n−M)=b0x(n)+b1x(n−1)+b2x(n−2)+....+bNx(n−N)
y=filter(b,a,x);
其中x为输入,b=[b0,b1,....bN],a=[a0,a1,.....,aM]b=[b_0,b_1,....b_N],a=[a_0,a_1,.....,a_M]b=[b0,b1,....bN],a=[a0,a1,.....,aM],
3.1 多阶4倍抽取CIC滤波器的实现
close all
clear all
clc
%set system parameter
fs = 1000; %The frequency of the local oscillator signal
Fs = 352800; %sampling frequency
Fs1 = 88200;
N = 24; %Quantitative bits
L = 81920;
%Generating an input signal
t =0:1/Fs:(1/Fs)*(L-1); %Generating the time series of sampling frequencies
sc1 =sin(2*pi*fs*t); %a sinusoidal input signal that produces a random starting phase
sc2 =sin(2*pi*Fs*t); %a sinusoidal input signal that produces a random starting phase
sc = sc1 +sc2;
%滑动平均滤波器
b =[1,-1];%comb
a =[1,-1];%integerator
i1 =filter(1,a,sc);
i2 =filter(1,a,i1);
i3 =filter(1,a,i2);
y = downsample(i3,4); %decimate
c1=filter(b,1,y);
c2=filter(b,1,c1);
c3=filter(b,1,c2);
sf = c3./64;
f_osc =fft(sc,L);
f_osc=20*log(abs(f_osc))/log(10); %换算成dBW单位
ft1=[0:(Fs/L):Fs/16]; %转换横坐标以Hz为单位
f_osc=f_osc(1:length(ft1));
f_o =fft(sf,L);
f_o=20*log(abs(f_o))/log(10); %换算成dBW单位
ft2=[0:(Fs1/L):Fs1/4]; %转换横坐标以Hz为单位
f_o=f_o(1:length(ft2));
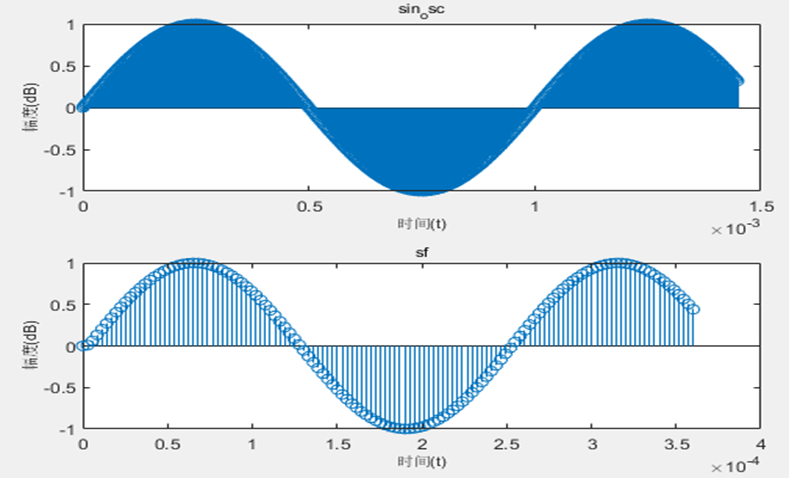
figure(1),
subplot(211),stem(t(1:512),sc(1:512));
xlabel('时间(t)','fontsize',8);
ylabel('幅度(dB)','fontsize',8);
title('sin_osc','fontsize',8);
subplot(212),stem(t(1:128),sf(1:128));
xlabel('时间(t)','fontsize',8);
ylabel('幅度(dB)','fontsize',8);
title('sf','fontsize',8);
figure(2),
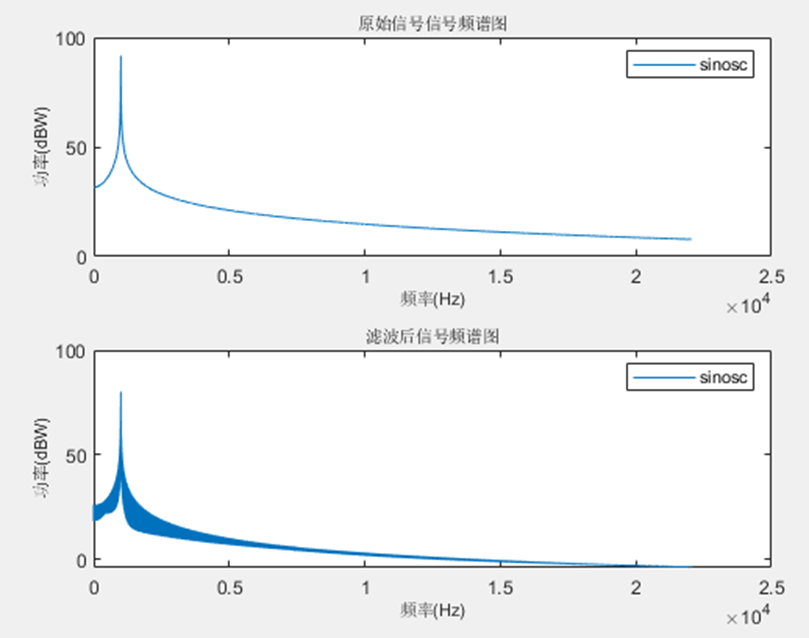
subplot(211),plot(ft1,f_osc);
xlabel('频率(Hz)','fontsize',8); ylabel('功率(dBW)','fontsize',8);
title('原始信号信号频谱图','fontsize',8);legend('sinosc');
subplot(212),plot(ft2,f_o);
xlabel('频率(Hz)','fontsize',8); ylabel('功率(dBW)','fontsize',8);
title('滤波后信号频谱图','fontsize',8);legend('sinosc');
3.2 多阶4倍插值CIC滤波器的实现
close all
clear all
clc
%set system parameter
fs = 1000; %The frequency of the local oscillator signal
Fs = 44100; %sampling frequency
Fs1 = 176400;
N = 24; %Quantitative bits
L = 81920;
%Generating an input signal
t =0:1/Fs:(1/Fs)*(L-1); %Generating the time series of sampling frequencies
sc =sin(2*pi*fs*t); %a sinusoidal input signal that produces a random starting phase
b =[1,-1];%comb
a =[1,-1];%integerator
%comb
c1=filter(b,1,sc);
c2=filter(b,1,c1);
c3=filter(b,1,c2);
y = upsample(c3,4);
%integerater
i1 =filter(1,a,y);
i2 =filter(1,a,i1);
i3 =filter(1,a,i2);
sf = i3./16;
f_osc =fft(sc,L);
f_osc=20*log(abs(f_osc))/log(10); %换算成dBW单位
ft1=[0:(Fs/L):Fs/2]; %转换横坐标以Hz为单位
f_osc=f_osc(1:length(ft1));
f_o =fft(sf,L);
f_o=20*log(abs(f_o))/log(10); %换算成dBW单位
ft2=[0:(Fs1/L):Fs1/8]; %转换横坐标以Hz为单位
f_o=f_o(1:length(ft2));
figure(1),
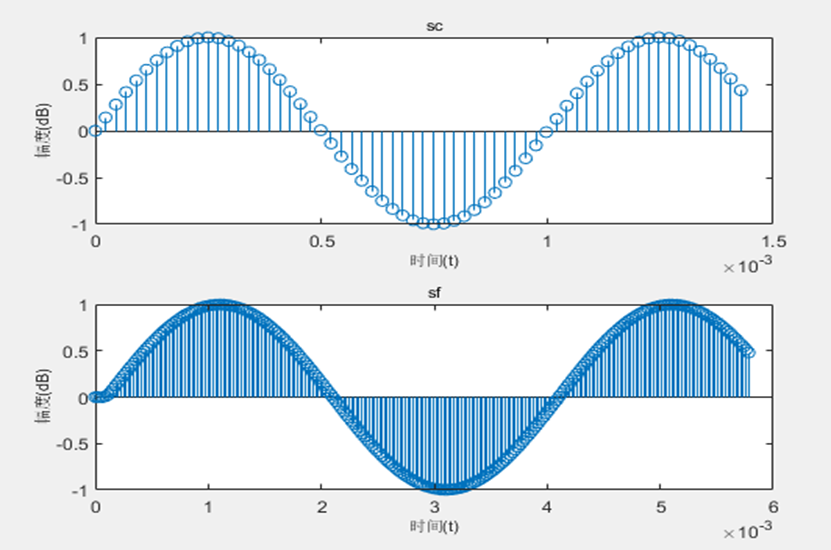
subplot(211),stem(t(1:64),sc(1:64));
xlabel('时间(t)','fontsize',8);
ylabel('幅度(dB)','fontsize',8);
title('sc','fontsize',8);
subplot(212),stem(t(1:256),sf(1:256));
xlabel('时间(t)','fontsize',8);
ylabel('幅度(dB)','fontsize',8);
title('sf','fontsize',8);
figure(2),
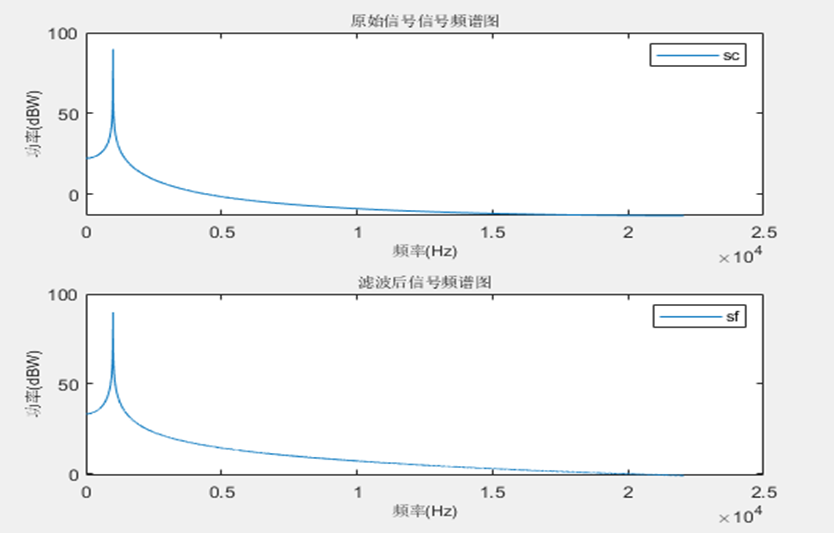
subplot(211),plot(ft1,f_osc);
xlabel('频率(Hz)','fontsize',8); ylabel('功率(dBW)','fontsize',8);
title('原始信号信号频谱图','fontsize',8);legend('sc');
subplot(212),plot(ft2,f_o);
xlabel('频率(Hz)','fontsize',8); ylabel('功率(dBW)','fontsize',8);
title('滤波后信号频谱图','fontsize',8);legend('sf');
3.3 多阶CIC滤波器的Verilog实现
设计一个5阶的3级CIC滤波器,对输入数据进行5倍抽取。根据上文抽取滤波器的结构,使用Verilog HDL分别完成积分模块、抽取模块、梳状模块的设计。
积分模块
由于积分运算会导致数据位宽扩展,首先需要确定积分器的输出数据位宽。可以借助如下公式,当输入信号为Bin位时,积分器最大可能输出位数为:B_max=[N〖log〗_2 (RD)+B_in].R为抽取/插值倍数,D为滤波器级数,N为滤波器阶数。本设计输入信号设置为10bit,则根据公式计算得到积分器输出数据为30Bits。
抽取模块
该模块的设计与上一篇中单级CIC的设计非常相似,只是不需要求和,每5个时钟周期抽出一个作为输出即可。同时设置一个输出有效信号,供下一级梳状模块使用。
梳状模块
该模块设计与积分模块很相似,只不过是由寄存器和减法器组成的。该模块的输出即为整个CIC抽取滤波器的输出数据,位宽可由如下公式确定:
符号意义与上文的公式相同,本例中经计算CIC滤波器的输出位宽最大为17Bits。
3级积分模块实现
`timescale 1ns / 1ps
//-----------------------------------------------------
//-----------------------------------------------------
module cic_Integrated(
input clk, //系统时钟2khz
input rst,
input signed [9:0] Xin,//数据输入频率为2khz
output signed [36:0] Xout //
);
wire signed [36:0] I1, I2, I3;
reg signed [36:0] d1, d2, d3;
//1th integrate,第一级积分器,v(n)=v(n-1)+x(n)
always @ (posedge clk or posedge rst)
begin
if (rst) d1 <= 37'd0;
else d1 <= I1; //
end
assign I1 = d1 + {{27{Xin[9]}},Xin}; //
//2th integrate,第2阶积分器
always @ (posedge clk or posedge rst)
begin
if (rst) d2 <= 37'd0;
else d2 <= I2; //
end
assign I2 = I1 + d2; //
//3th..第3阶积分器
always @ (posedge clk or posedge rst)
begin
if (rst) d3 <= 37'd0;
else d3 <= I3; //??
end
assign I3 = I2 + d3; //
assign Xout = I3; //
endmodule
5倍抽取模块实现
`timescale 1ns / 1ps
module cic_Decimate
(
input clk, //50MHz
input rst, //????
input signed [36:0] din, //系统时钟2khz
output rdy, //数据输入频率2khz
output signed [36:0] dout
);
reg rdy_tem;
reg [2:0] cnt;
reg signed [36:0] dout_tem;
always @ (posedge clk or posedge rst)
begin
if (rst)
begin
cnt <= 3'd0;
rdy_tem <= 1'b0;
dout_tem <=37'd0;
end
else
begin
if (cnt == 4)
begin //??4???
rdy_tem <= 1'b1;
dout_tem <= din; //??????
cnt <= 'd0;
end
else
begin
rdy_tem <= 1'b0;
cnt <= cnt + 1'b1;
end
end
end
assign dout = dout_tem;
assign rdy = rdy_tem;
endmodule
3阶梳状模块实现
`timescale 1ns / 1ps
module cic_comb
(
input clk, //系统时钟2khz
input rst, //
input signed [36:0] din, //输入数据频率2khz
input RDY, //输入的数据准备好信号
output signed [16:0] dout
);
reg signed [36:0] d1,d2,d3,d4;
wire signed [36:0] C1, C2;
wire signed [36:0] dout_tem;
always @ (posedge clk or posedge rst)
if (rst) begin
d1 <= 37'd0; d2 <= 37'd0; d3 <= 37'd0; d4 <= 37'd0;
end
else begin
if (RDY) begin //
d1 <= din; //
d2 <= d1;
d3 <= C1;
d4 <= C2;
end
end
assign C1 = (rst?37'd0:(d1 - d2)); // y(n)=v(n)-v(n-1)
assign C2 = (rst?37'd0:(C1 - d3)); // z(n)=y(n)-y(n-1)
assign dout_tem = (rst?37'd0:(C2 - d4)); //w(n)=z(n)-z(n-1)
assign dout = dout_tem[16:0]; //取低16位作为输出
endmodule
4顶层模块
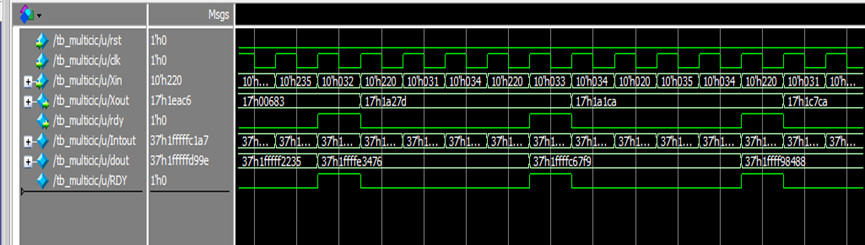
module multicic (
input rst,
input clk,
input signed [9:0] Xin,
output signed [16:0] Xout, //
output rdy
);
wire signed [36:0]Intout;
wire signed [36:0]dout;
wire RDY;
cic_Integrated u1(
.rst(rst),
.clk(clk),
.Xin(Xin),
.Xout(Intout)
);
cic_Decimate u2(
.clk(clk),
.rst(rst),
.din(Intout),
.rdy(RDY),
.dout(dout)
);
cic_comb u3(
.clk(clk),
.rst(rst),
.din(dout),
.RDY(RDY),
.dout(Xout)
);
assign rdy=RDY;
endmodule
4.半带滤波器
半带滤波器是一种实现数字下变频的滤波器,
(1)半带滤波器的通带和阻带对称,即通带容限和阻带容限相等,即δp=δs,且Ws=π−Wp,Ws为阻带截止频率,Wpδ_p=δ_s,且W_s=π-W_p,W_s为阻带截止频率,Wpδp=δs,且Ws=π−Wp,Ws为阻带截止频率,Wp为通带截止频率。即通带边频Fp和阻带边频Fs满足Fp+Fs=fs/2,(fs为输入数据的采样频率)F_p和阻带边频F_s满足F_p+F_s=f_s/2,(f_s为输入数据的采样频率)Fp和阻带边频Fs满足Fp+Fs=fs/2,(fs为输入数据的采样频率)。
(2)为了保证FIR滤波器的线性相位特性,滤波器的系数具有偶对称特性。即要求h(n)=h(N-1-n);这里N为滤波器的阶数(滤波器长度为偶数,长度是滤波器阶数加1),设N为奇数。滤波器的系数除了(N-1)/2+1外,所有的偶次系数均为0.系数对称且近一半系数为0.从而大大降低了乘法和加法运算次数。
(3)H(ej(π−w))H(e^{j(π-w)})H(ej(π−w))为2倍抽取后(抽样频率降低一半)后滤波器以π为周期的频率响应,因此经半带滤波器滤波后,进行2倍抽取时,信号通带内没有频谱混叠,但过渡带内有频谱混叠。
(4)根据半带滤波器的频率特性, Fs=fs/2−FpF_s=f_s/2- F_pFs=fs/2−Fp,即滤波器的过渡带∆F=Fs−Fp=fs/2−2Fp∆F=F_s-F_p=f_s/2- 2F_p∆F=Fs−Fp=fs/2−2Fp,当信号的通带FpF_pFp很小时,这种过渡带对于最后一级来说往往过大,不能满足滤波特性的总体要求,因此不适合作为多级抽取滤波器的最后一级,即后级滤波器必须有其他类型的FIR滤波器,对于后级FIR滤波器来说,信号经过前级的CIC、半带滤波抽取后,采样速率相对来讲已经很低了,所以在一定的处理时钟下,需要采用更高阶的一般频率特性的FIR滤波器,使其通带波动,过渡带宽,阻带衰减特性等设计指标能设计得更高。
多级半带滤波器的设计
1.各级半带滤波器的总体设计要求
在多级半带滤波器系统中,因每级滤波器均需要进行2倍抽取,因此各级滤波器具体的通、阻带频率及过渡带频率均不相同。为便于讨论,采样滤波器的真实频率,而不是归一化频率。且各级要求半带滤波器的通带容限和阻带容限相等,因此可令容限δ:
δ=min(δpi,δs)=(δp/K,δs)δ=min(δ_{pi},δ_s)=(δ_p/K,δ_s)δ=min(δpi,δs)=(δp/K,δs),其中K为抽取系统的总的级数,δsδ_sδs为抽取系统总的阻带误差容限,δp/Kδ_p/Kδp/K为各级半带滤波器的通带误差容限δpiδ_{pi}δpi,
它等于整个抽取系统通带误差容限δ_p的1/K。多级2倍抽取系统的总级数K为:K=log2(D).D为抽取系统总的抽取因子。
假设抽取器最后输出的信号为xk(nkTk)x_k (n_k T_k)xk(nkTk),信号抽取率为Fk=1/TkF_k=1/T_kFk=1/Tk,信号要求滤波器的通带上限边缘频率为fpf_pfp,阻带下限边缘频率为fs,为了避免混叠,取fs≤Fk/2f_s≤F_k/2fs≤Fk/2.这是多级实现最后一级(即第K级)对对滤波器的通带和阻带的频率要求,至于前面的任何一级,第i级(i=1,2,…K-1),为降低滤波器的阶次,有意加大其过渡带,通带仍为fpf_pfp,但阻带下限边缘频率为fsi可超过Fi/2f_{si}可超过F_i/2fsi可超过Fi/2。
这种情况下有两种可能方案:
其一是允许i=1到K-1级中的滤波器在fp≤f≤fsi的频率范围内允许有混叠,但要保护0≤f≤fp0≤f≤f_p0≤f≤fp的频率范围内不允许有混叠。
其二是各级滤波器在0≤f≤fsi的频率范围内不允许有混叠。
4.1 允许过渡带有混叠的设计
第i级中半带滤波器的通帯上限边缘频率与系统的通带频率相同,均为fp,其阻带下限边缘频率则与滤波器位于第几级有关。设第i级滤波器的抽样率为Fi−1F_{i-1}Fi−1,第i级经过抽取后的抽样率为Fi=Fi−1/2=F0/2iF_i=F_{i-1}/2=F_0/2^iFi=Fi−1/2=F0/2i,其中F0F_0F0为整个抽取系统输入信号的频率。图6-26为第i级滤波器的幅频响应图,虚线部分为抽取之后抽样率为F时滤波器幅频响应在一个周期中的对称部分。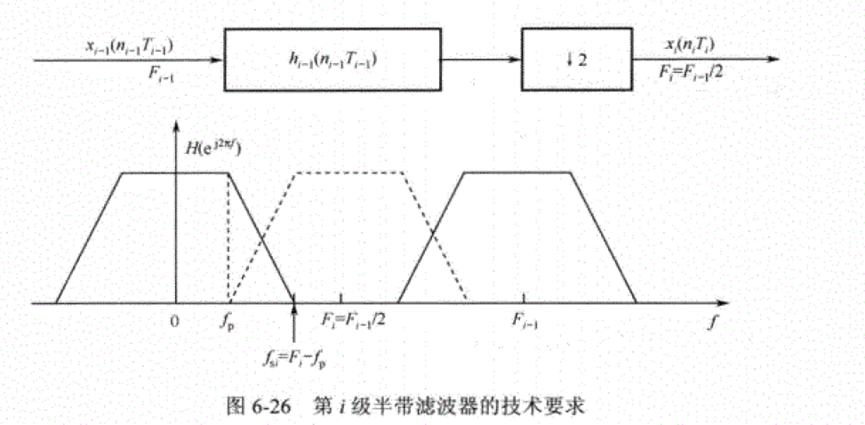
根据上面的说明,可以得出各级半带滤波器的技术参数如下所述。
通带上限频率为:fpi=fp,i=1,2,....Kf_{pi}=f_p,i=1,2,....Kfpi=fp,i=1,2,....K
阻带下限频率为:fsi=Fi−1/2−fp=Fi−fp,i=1,2,....K−1f_{si}=F_{i-1}/2-f_p=F_i-f_p,i=1,2,....K-1fsi=Fi−1/2−fp=Fi−fp,i=1,2,....K−1
第i级输出信号的抽样率为:Fi=Fi−1/2=F0/2iF_i=F_{i-1}/2=F_0/2^iFi=Fi−1/2=F0/2i
正如前面所述,最后一级滤波器与前面K-1级稍有不同,因为最后一级滤波器的阻带下限边缘频率最高不能超过F_K/2,为减小过渡带中的混叠,fsK=FK/2f_{sK}=F_K/2fsK=FK/2而不等于FK−fpF_K-f_pFK−fp。正是由于这个缘故,最末一级滤波器不是半带滤波器,所以不能按照半带滤波器的方法进行设计
4.2不允许过渡带有混叠的设计
根据前面所述的设计方法设计滤波器,第i级滤波器的过渡带:fsi=Fi−fpf_{si}=F_i-f_pfsi=Fi−fp内一定有频谱混叠。为了保护在频带0≤f≤fs0≤f≤f_s0≤f≤fs内都没有混叠,我们可以将系统的阻带频率f_s当作系统及各级滤波器的通带频率f_p,这样根据半带滤波器的频率特性,可保证半带滤波器的通带没有混叠,同时也保证了系统的过渡带内没有混叠。经过这样的变换后,各级半带滤波器的阻带下限边缘频率:fsi=Fi−1/2−fp=Fi−fsf_{si}=F_{i-1}/2-f_p=F_i-f_sfsi=Fi−1/2−fp=Fi−fs。
这样,在设计中保护了整个系统的通带及过渡带(0≤f≤f_s)不受混叠,代价则是降低了各级半带滤波器的过渡带带宽(由Fi−fpF_i-f_pFi−fp降低为Fi−fsF_i-f_sFi−fs),致使滤波器的阶数增加。过渡带不受混叠条件下第i级(不包括最后一级)滤波器的技术要求总结如下:
通带和阻带误差容限δ=min(δpi,δs)=(δp/K,δs)δ=min(δ_{pi},δ_s)=(δ_p/K,δ_s)δ=min(δpi,δs)=(δp/K,δs)
通带上限边缘频率为fpf_pfp,在设计中没有使用该项参数:
阻带下限边缘频率fsi=Fi−fsf_{si}=F_i-f_sfsi=Fi−fs
其中δp,δs,fp和fsδ_p,δ_s,f_p和f_sδp,δs,fp和fs是给定的系统设计指标,Fi=F0/2i,F0F_i=F_0/2^i,F_0Fi=F0/2i,F0是系统输入信号的频率。
最后一级滤波器不是半带滤波器,其通带上限边缘频率为fp,通带误差容限为δp/K,阻带下限边缘频率为fs,阻带误差容限为δsf_p,通带误差容限为δ_p/K,阻带下限边缘频率为f_s,阻带误差容限为δ_sfp,通带误差容限为δp/K,阻带下限边缘频率为fs,阻带误差容限为δs。这个滤波器的设计按照一般滤波器的设计方法进行
4.3多级半带滤波器的FPGA实现
为便于讨论多级半带滤波器的详细设计过程,我们仍以一个具体的工程实例来进行讲解。
例:在某一数字信号处理系统中,输入信号采样频率F=3200Hz,数据位宽为10比特,有用信号的通带截止频率fp=20Hzf_p=20Hzfp=20Hz,阻带截止频率fs=25Hzf_s=25Hzfs=25Hz,要求将信号的抽样率减小到50Hz,使用多级半带滤波器实现此抽取系统,系统的通带容限和阻带容限均为0.001,采用FPGA实现此抽取系统,并使用 MATLAB对抽取系统的实现结果进行仿真测试。
1.各级半带滤波器的性能指标设计及 MATLAB仿真
首先,我们需要根据实例工程的系统指标要求,合理设计各级滤波器的指标要求,然后使用 MATLAB软件提供的函数设计出各级滤波器的系数,最后使用FPGA进行实现。根据实例要求容易获取系统的总抽取因子,有D=F0/FK=3200/50=64=26D=F_0/F_K=3200/50=64=2^6D=F0/FK=3200/50=64=26,也就是说,可以使用6級滤波器实现该抽取系统,其中前5级为半带滤波器,最末一级采用普通FIR滤波器。
5.抽取系统的FPCA设计与实现
采用 MATLAB设计出各级滤波器的系数后,即可采用第4章讲述的方法设计各级滤波器,并将各级滤波器进行级联形成完整的抽取系统。由于半带滤波器本质上是FIR滤波器,因此半带滤波器的FPGA实现与普通的FIR滤波器实现没有什么差别。需要注意的是,由于半带滤波器的部分系数为0,因此可以节省部分乘法及加法运算。
本实例采用 Quartus提供的 FIR Compiler vl.2.1核来实现各级半带滤波器及最末一级滤波器。 Quartus提供的 FIR Compiler VI2.1核功能十分强大,本身即支持半带滤波器设计,使用起来十分方便。
在编写顶层文件时,需要注意的是如何合理确定各级滤波器输入输出数据位宽。当输入数据位宽、滤波器系数位宽、滤波器长度确定后,全精度运算的输出数据位宽也就随之确定了(FR核对应的参数为 output rounding mode=Full Precision)在本实例中,如果各级滤波器均要保持全精度运算结果,则容易计算得出抽取系统的最终输出数据需要用102比特来表示(输入数据为8比特,滤波器系数均为12比特)。这样高的位数不仅要占用大量的寄存器资源,也会降低系统运算速度。实际上FIR核的输入数据位宽最高只支持32比特。因此,在各级滤波器的FPGA实现时,必须对输出数据进行截位。
有效截位的一条重要原则是尽量保留多的有效数据位。
先看第一级滤波器的输出数据位宽。采用 MATLAB仿真,很容易得出输出数据最大绝对值是输入数据的3243倍,小于212倍。也就是说输出数据位宽取输入数据位宽加上12比特即可。第1级FIR核的输出数据位宽为20比特,有效数据位为19~0比特,取全部20位作为下一级滤波器的输入。
第2级滤波器输入位宽为20比特。采用同样的方法,经 MATLAB仿真得出,输出数据位宽取输入数据位宽加上12比特。FIR核生成的输出数据为32比特,有效数据位为0~31比特,取全部32比特为下一级滤波器的输入。
第3级滤波器输入位宽为32比特,仿真得出有效数据输出为44比特。FIR核生成的输出数据为45比特。由于FIR核最大输入数据位数为32,因此取输出数据的43~12比特为下一级滤波器的输入。
第4级滤波器输入位宽为32比特,仿真得出有效数据输出为44比特。FIR核生成的输出数据为45比特。由于FIR核最大输入数据位数为32,因此取输出数据的43~12比特为下一级滤波器的输入。
第5级滤波器输入位宽为32比特,仿真得出有效数据输出为44比特。FIR核生成的输出数据为45比特。由于FIR核最大输入数据位数为32,因此取输出数据的43~12比特为下一级滤波器的输入。
第6级滤波器输入位宽为32比特,仿真得出有效数据输出为44比特。FR核生成的输
出数据为46比特。输出数据位宽设为20比特,取输出数据的43~24为最终输出数据。
确定好各级滤波器的输入输出数据位宽,以及截位方案后,编写整个抽取系统的顶层文件就十分简单了。

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)