C语言数据结构_哈夫曼树
哈夫曼树构造哈夫曼树声明单个结点的信息:权值weight,父节点parent,左孩子lc,右孩子rc组成。以权值分别为4 2 5 9举例第一阶段:我们利用数组的方式来构造哈夫曼树,申请2 * n + 1个内存空间用来存储每一个树结点,注意在存储数据的时候从下标为1开始存储。依次将n个权值分别存储在数组中,parent,lc,rc分别赋值为0。第二阶段:1、在下标为1-4的权值中找到两个权值最小的,
哈夫曼树
构造哈夫曼树
声明单个结点的信息:权值weight,父节点parent,左孩子lc,右孩子rc组成。
以权值分别为4 2 5 9举例
第一阶段:
我们利用数组的方式来构造哈夫曼树,申请2 * n + 1个内存空间用来存储每一个树结点,注意在存储数据的时候从下标为1开始存储。依次将n个权值分别存储在数组中,parent,lc,rc分别赋值为0。
第二阶段:
1、在下标为1-4的权值中找到两个权值最小的,并且父结点为0。
2、将这两个权值相加形成新的权值并赋值给下标为5的树。
3、选取的结点父结点赋值为5.
4、下标为5的左孩子为选取的结点中权值最小的下标,右孩子为另一个结点的下标。
1、在下标为1-5的权值中找到两个权值最小的,并且父结点为0。
2、将这两个权值相加形成新的权值并赋值给下标为6的树。
3、选取的结点父结点赋值为6.
4、下标为6的左孩子为选取的结点中权值最小的下标,右孩子为另一个结点的下标。
1、在下标为1-6的权值中找到两个权值最小的,并且父结点为0。
2、将这两个权值相加形成新的权值并赋值给下标为7的树。
3、选取的结点父结点赋值为7.
4、下标为7的左孩子为选取的结点中权值最小的下标,右孩子为另一个结点的下标。
编码
1、开辟n + 1个空间HC用来存储每一个权值的编码,构造一个辅助的数组来暂时存储权值的编码。
2、将辅助数组的末尾赋值为空,申请一个指针start指向辅助数组的末尾。
3、找到下标为1的树的父结点,如果父结点的左孩子为该树的下标,则辅助数组存储数字0,如果父结点的右孩子为该树的下标,则辅助数组存储数字1。
4、以上一步骤的父结点为新的下标继续重复步骤三,直至父结点为0。
5、将辅助数组的值赋值给HC
例如权值4的编码为111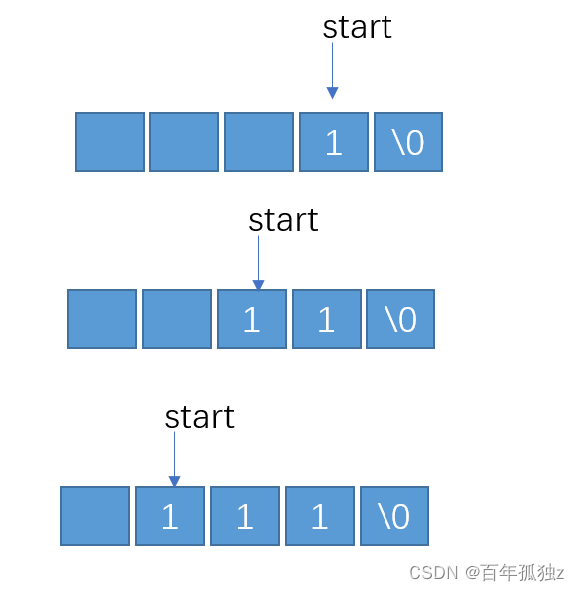
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef double DataType; //结点权值的数据类型
typedef struct HTNode //单个结点的信息
{
DataType weight; //权值
int parent; //父节点
int lc, rc; //左右孩子
} * HuffmanTree;
typedef char **HuffmanCode; //字符指针数组中存储的元素类型
//在下标为1到i-1的范围找到权值最小的两个值的下标,其中s1的权值小于s2的权值
void Select(HuffmanTree &HT, int n, int &s1, int &s2)//c++中&s1等于传进来的参数可以在函数中对s1进行操作类似于指针的作用
{
int min;
//找第一个最小值
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0)
{
min = i;
break;
}
}
for (int i = min + 1; i <= n; i++)
{
if (HT[i].parent == 0 && HT[i].weight < HT[min].weight)
min = i;
}
s1 = min; //第一个最小值给s1
//找第二个最小值
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0 && i != s1)
{
min = i;
break;
}
}
for (int i = min + 1; i <= n; i++)
{
if (HT[i].parent == 0 && HT[i].weight < HT[min].weight && i != s1)
min = i;
}
s2 = min; //第二个最小值给s2
}
//构建哈夫曼树
void CreateHuff(HuffmanTree &HT, DataType *w, int n)
{
int m = 2 * n - 1; //哈夫曼树总结点数
HT = (HuffmanTree)calloc(m + 1, sizeof(HTNode)); //开m+1个HTNode,因为下标为0的HTNode不存储数据
for (int i = 1; i <= n; i++)
{
HT[i].weight = w[i - 1];//赋权值给n个叶子结点
HT[i].lc = 0;
HT[i].rc = 0;
HT[i].parent = 0;
}
for (int i = n + 1; i <= m; i++) //构建哈夫曼树
{
//选择权值最小的s1和s2,生成它们的父结点,s1,s2分别为最小权值和次小权值的下标
int s1, s2;
Select(HT, i - 1, s1, s2); //在下标为1到i-1的范围找到权值最小的两个值的下标,其中s1的权值小于s2的权值
HT[i].weight = HT[s1].weight + HT[s2].weight; // i的权重是s1和s2的权重之和
HT[s1].parent = i; // s1的父亲是i
HT[s2].parent = i; // s2的父亲是i
HT[i].lc = s1; //左孩子是s1
HT[i].rc = s2; //右孩子是s2
}
//打印哈夫曼树中各结点之间的关系
printf("哈夫曼树为:>\n");
printf("下标 权值 父结点 左孩子 右孩子\n");
printf("0 \n");
for (int i = 1; i <= m; i++)
{
printf("%-4d %-6.2lf %-6d %-6d %-6d\n", i, HT[i].weight, HT[i].parent, HT[i].lc, HT[i].rc);
}
printf("\n");
}
//生成哈夫曼编码
void HuffCoding(HuffmanTree &HT, HuffmanCode &HC, int n)
{
HC = (HuffmanCode)malloc(sizeof(char *) * (n + 1)); //开n+1个空间,因为下标为0的空间不用
char *code = (char *)malloc(sizeof(char) * n); //辅助空间,编码最长为n(最长时,前n-1个用于存储数据,最后1个用于存放'\0')
code[n - 1] = '\0'; //辅助空间最后一个位置为'\0'
for (int i = 1; i <= n; i++)
{
int start = n - 1; //每次生成数据的哈夫曼编码之前,先将start指针指向'\0'
int c = i; //正在进行的第i个数据的编码
int p = HT[c].parent; //找到该数据的父结点
while (p) //直到父结点为0,即父结点为根结点时,停止
{
if (HT[p].lc == c) //如果该结点是其父结点的左孩子,则编码为0,否则为1
code[--start] = '0';
else
code[--start] = '1';
c = p; //继续往上进行编码
p = HT[c].parent; // c的父结点
}
HC[i] = (char *)malloc(sizeof(char) * (n - start)); //开辟用于存储编码的内存空间
strcpy(HC[i], &code[start]); //将编码拷贝到字符指针数组中的相应位置
}
free(code); //释放辅助空间
}
//主函数
int main()
{
int n = 0;
printf("请输入数据个数:>");
scanf("%d", &n);
DataType *w = (DataType *)malloc(sizeof(DataType) * n);
if (w == NULL)
{
printf("malloc fail\n");
exit(-1);
}
printf("请输入数据:>");
for (int i = 0; i < n; i++)
{
scanf("%lf", &w[i]);
}
HuffmanTree HT;
CreateHuff(HT, w, n); //利用数组构建哈夫曼树
HuffmanCode HC;
HuffCoding(HT, HC, n); //构建哈夫曼编码
for (int i = 1; i <= n; i++) //打印哈夫曼编码
{
printf("数据%.2lf的编码为:%s\n", HT[i].weight, HC[i]);
}
free(w);
return 0;
}
运算结果
请输入数据个数:>4
请输入数据:>4
2
5
9
哈夫曼树为:>
下标 权值 父结点 左孩子 右孩子
0
1 4.00 5 0 0
2 2.00 5 0 0
3 5.00 6 0 0
4 9.00 7 0 0
5 6.00 6 2 1
6 11.00 7 3 5
7 20.00 0 4 6
数据4.00的编码为:111
数据2.00的编码为:110
数据5.00的编码为:10
数据9.00的编码为:0
PS D:\Data Struction\weekFive\student>
哈夫曼树的实际应用
以下为涂然学长的代码,因为该代码运用了文件访问的功能所以在运行是应该在代码相同的路径上创建一个data.txt的文件。code.txt用来存储data文件转换的哈夫曼编码,out.txt用来存储code.txt文件里面的哈夫曼编码的解码数据,另外code.txt和out.txt系统会自动创建不需要自己创建。
/*
Descripttion:
Version: 1.0
Author: 涂然 18计科3班
Date: 2021-05-31 9:00:00
*/
#include <iostream>
#include <fstream>
#include <string.h>
using namespace std;
#define MaxSize 1024 // 读入文件的上限
#define OK 1
#define ERROR 0
typedef int Status;
typedef struct wordcnt{ // 统计字符和对应的次数
char ch;//存储字母
int cnt = 0;//一串字符串中ch出现的个数
}Count;
typedef struct NumCount{ // 统计次数的外部封装
Count count[MaxSize];//对每一个不同的字母进行封装
int length = 0;//不同字母的个数
}NumCount;
typedef struct HTree{ // 哈夫曼树结构
char data;
int weight;
int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef struct HCode{ // 编码结构
char data;
char* str;
}*HuffmanCode;
Status ReadData(char *source); // 读入文件
Status WordCount(char *data,NumCount *paraCnt); // 统计次数
Status Show(NumCount *paraCnt); // 展示次数
Status CreateHuffmanTree(HuffmanTree &HT,int length,NumCount cntarray); // 创建哈夫曼树
Status select(HuffmanTree HT,int top,int *s1,int *s2); // 选择权重最小的两个节点
Status CreateHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int length); // 创建哈夫曼编码
Status Encode(char *data,HuffmanCode HC,int length); // 将读入的文件编码,写到txt文件
Status Decode(HuffmanTree HT,int length); //读入编码文件,解码
int main(int argc, char** argv) {
char data[MaxSize];
NumCount Cntarray;
ReadData(data); // 读入数据
WordCount(data,&Cntarray); // 统计次数
Show(&Cntarray); //可以查看每个单词出现的对应次数
HuffmanTree tree;
CreateHuffmanTree(tree,Cntarray.length,Cntarray); // 建树
HuffmanCode code;
CreateHuffmanCode(tree,code,Cntarray.length); // 创建编码
Encode(data,code,Cntarray.length); // 生成编码文件
Decode(tree,Cntarray.length); // 解码
cout<<"Please view the generated TXT file to check the result"<<endl;
return 0;
}
Status ReadData(char *source)
{
//打开文件读入数据
ifstream infile;
infile.open("data.txt");
cout<<"Reading..."<<endl;
cout<<"the input file is:"<<endl;
infile.getline(source,MaxSize);
cout<<source<<endl;
infile.close();
cout<<endl;
return OK;
}
Status WordCount(char *data,NumCount *paraCnt)
{
int flag;// 标识是否已经记录
int len = strlen(data);
for(int i = 0;i < len;++i)
{
flag = 0;
for(int j = 0;j < paraCnt->length;++j)
{
if(paraCnt->count[j].ch == data[i]) // 若已有记录,直接++
{
++paraCnt->count[j].cnt;
flag = 1;
break;
}
}
if(!flag) // 没有记录,则新增
{
paraCnt->count[paraCnt->length].ch = data[i];
++paraCnt->count[paraCnt->length].cnt;
++paraCnt->length;
}
}
return OK;
}
Status Show(NumCount *paraCnt)
{
cout<<"the length is "<<paraCnt->length<<endl;
for(int i = 0;i < paraCnt->length;++i)
{
cout<<"The character "<<paraCnt->count[i].ch<<" appears "<<paraCnt->count[i].cnt<<endl;
}
cout<<endl;
return OK;
}
Status CreateHuffmanTree(HuffmanTree &HT,int length,NumCount cntarray)
{
if(length <= 1) return ERROR;
int s1,s2;
int m = length*2-1; // 没有度为1的节点,则总结点是2*叶子节点数-1个
HT = new HTNode[m+1]; //分配m+1个空间,实际上是m+1个树
for(int i = 1;i <= m;++i) // 初始化
{
HT[i].parent = 0;
HT[i].lchild = 0;
HT[i].rchild = 0;
}
for(int i = 1;i <= length;++i)
{
HT[i].data = cntarray.count[i-1].ch;
HT[i].weight = cntarray.count[i-1].cnt;
}
for(int i = length + 1;i <= m;++i)
{
select(HT,i-1,&s1,&s2); // 从前面的范围里选择权重最小的两个节点
HT[s1].parent = i;
HT[s2].parent = i;
HT[i].lchild = s1;
HT[i].rchild = s2;
HT[i].weight = HT[s1].weight + HT[s2].weight; // 得到一个新节点
}
return OK;
}
Status select(HuffmanTree HT,int top,int *s1,int *s2)
{
int min = INT_MAX;
for(int i = 1;i <= top;++i) // 选择没有双亲的节点中,权重最小的节点
{
if(HT[i].weight < min && HT[i].parent == 0)
{
min = HT[i].weight;
*s1 = i;
}
}
min = INT_MAX;
for(int i = 1;i <= top;++i) // 选择没有双亲的节点中,权重次小的节点
{
if(HT[i].weight < min && i != *s1 && HT[i].parent == 0)
{
min = HT[i].weight;
*s2 = i;
}
}
return OK;
}
Status CreateHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int length)
{
HC = new HCode[length+1];//分配length+1个空间用来存储不同字母对应的编码
char *cd = new char[length]; // 存储编码的临时空间
cd[length-1] = '\0'; // 方便之后调用strcpy函数
int c,f,start;
for(int i = 1;i <= length;++i)
{
start = length-1; // start表示编码在临时空间内的起始下标,由于是从叶子节点回溯,所以是从最后开始
c = i;
f = HT[c].parent;
while(f != 0)
{
--start; // 由于是回溯,所以从临时空间的最后往回计
if(HT[f].lchild == c)
cd[start] = '0';
else
cd[start] = '1';
c = f;
f = HT[c].parent;
}
HC[i].str = new char[length-start]; // 最后,实际使用的编码空间大小是length-start
HC[i].data = HT[i].data;
strcpy(HC[i].str,&cd[start]); // 从实际起始地址开始,拷贝到编码结构中
}
delete cd;
}
Status Encode(char *data,HuffmanCode HC,int length)
{
ofstream outfile;
outfile.open("code.txt");
for(int i = 0;i < strlen(data);++i) // 依次读入数据,查找对应的编码,写入编码文件
{
for(int j = 1;j <= length;++j)
{
if(data[i] == HC[j].data)
{
outfile<<HC[j].str;
}
}
}
outfile.close();
cout<<"the code txt has been written"<<endl;
cout<<endl;
return OK;
}
Status Decode(HuffmanTree HT,int length)
{
char *codetxt = new char[MaxSize * length];
ifstream infile;
infile.open("code.txt");
infile.getline(codetxt,MaxSize*length);
infile.close();
ofstream outfile;
outfile.open("out.txt");
int root = 2*length-1; // 从根节点开始遍历
for(int i = 0;i < strlen(codetxt);++i)
{
if(codetxt[i] == '0') root = HT[root].lchild; //为0表示向左遍历
else if(codetxt[i] == '1') root = HT[root].rchild; //为1表示向右遍历
if(HT[root].lchild == 0 && HT[root].rchild == 0) // 如果已经是叶子节点,输出到输出文件中,然后重新回到根节点
{
outfile<<HT[root].data;
root = 2*length-1;
}
}
outfile.close();
cout<<"the output txt has been written"<<endl;
cout<<endl;
return OK;
}
运行结果
^
Reading...
the input file is:
Life is full of confusing and disordering Particular time,a particular location,Do the arranged thing of ten million time in the brain,Step by step ,the life is hard to avoid delicacy and stiffness No enthusiasm forever,No unexpected happening of surprising and pleasing So,only silently ask myself in mind Next happiness,when will come?
the length is 31
The character L appears 1
The character i appears 30
The character f appears 11
The character e appears 28
The character appears 50
The character s appears 18
The character u appears 7
The character l appears 16
The character o appears 17
The character c appears 8
The character n appears 26
The character g appears 7
The character a appears 20
The character d appears 11
The character r appears 14
The character P appears 1
The character t appears 18
The character m appears 7
The character , appears 7
The character p appears 10
The character D appears 1
The character h appears 9
The character b appears 2
The character S appears 2
The character y appears 5
The character v appears 2
The character N appears 3
The character x appears 2
The character k appears 1
The character w appears 2
The character ? appears 1
the code txt has been written
the output txt has been written
Please view the generated TXT file to check the result
PS D:\Data Struction\weekFive\teacher>

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容








所有评论(0)