实验5  二叉树的基本操作

一、实验目的

 熟练应用二叉链表存储结构，实现二叉树的构建，遍历等操作。

二、实验软硬件要求

硬件：一台安装了windows操作系统的计算机。

软件：C语言编程工具

• 实验内容（需写出源程序）

【问题描述】

假设有一段电文由字符集 {A, B, C, D, E, F, G, H} 中的字符组成，各字符在电文中出现的频率由对应次数集 {5，29，7，8，14，23，3，11} 中的数字表示，请设计各字符的哈夫曼编码。

【基本要求】

应包含以下几方面的功能：

1. 设计哈夫曼树。具体构造方法如下：以字符集{A, B, C, D, E, F, G, H} 中的字符作为叶子结点，以各字符在次数集 {5，29，7，8，14，23，3，11} 中对应的次数作为各叶子结点的权值构造一棵哈夫曼树。
2. 设计哈夫曼编码。按照构造出来的哈夫曼树，规定哈夫曼树的左分支为0，右分支为1，则从根结点到每个叶子结点所经过的分支对应的0和1组成的序列便为该结点对应字符的哈夫曼编码。
3. 依次求出每个字符的哈夫曼编码并输出。

#include<bits/stdc++.h>

#include<iostream>

using namespace std;

typedef struct{

       int weight;

       int parent,lchild,rchild;

}HTNode,*HuffmanTree;

typedef char **HuffmanCode;//动态分配数组存储哈夫曼编码表

void CreateHuffmanTree(HuffmanTree &HT,int n);   //构造哈夫曼树

void Select(HuffmanTree HT,int end,int *s1,int *s2);  //select函数

void CreateHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int n); //哈夫曼编码

void CreateHuffmanTree(HuffmanTree& HT,int n){

       //构造哈夫曼树

       if(n<=1)  return;

       int m=2*n-1;

       HT=new HTNode[m+1]; //0单元号未用，下标从1开始

       for(int i=1;i<=m;i++){ //初始化，将下标1~m号结点的双亲，左孩子，右孩子置为0

              HT[i].parent=0;

              HT[i].lchild=0;

              HT[i].rchild=0;

       }

       for(int i=1;i<=n;i++){

              cin >> HT[i].weight;  //输入前n个结点的权值

       }

// 初始化结束，下面创开始创建哈夫曼树

//---------------------------------------------------------

 for(int i=n+1;i<=m;i++){

      /* 在select函数中，在前n个结点中通过n-1次的选择两个权值较小的结点,

        进行合并，删除 来创建哈夫曼树 */

        int s1=0,s2=0;

      Select(HT,i-1,&s1,&s2);

      /* 在select中挑选出两个权值较小的结点，且s1<s2；

        合并成一个新的结点，新的结点的结点号为i ,此时s1和s2结点的双亲结点即为i */

      HT[s1].parent=i; HT[s2].parent=i;

      HT[i].lchild=s1;//将s1和s2分别作为结点i的左右孩子

      HT[i].rchild=s2;

      HT[i].weight=HT[s1].weight+HT[s2].weight;//结点i的权值为左右孩子之和

 }

}

//Select函数

void Select(HuffmanTree HT,int end,int *s1,int *s2){

       int min1,min2;//min1存放较小的，min2存放第二小的,min1<min2

       //先挑选出一个双亲结点为0的结点 ，如果双亲节点不为0说明这个结点已经在生成新节点中被使用过

       int i=1;

       while(HT[i].parent!=0&&i<=end){

              i++;

       }

       //将第一次挑选出来的结点的权值先赋值给min1，然后i加一，挑选第二个双亲结点为0的结点

       min1=HT[i].weight;

       *s1=i;

       i++;

       // 挑选第二个双亲结点为0的结点

       while(HT[i].parent!=0&&i<=end){

              i++;

       }

       /*对挑选出来的第一个结点第二个结点再进行权值的比较，如果第二次挑选出来的HT[i].weight

       小于min1的值，则先将min1的值付给min2,再将HT[i].weight赋给min1; 如果第二次挑选出来的

       HT[i].weight大于min1的值，则将HT[i].weight赋给min2

       */

       if(HT[i].weight<min1){

              min2=min1;

              *s2=*s1;

              min1=HT[i].weight;

              *s1=i;

       }else{

              min2=HT[i].weight;

              *s2=i;

       }

       //对余下的结点进行遍历

       for(int j=i+1;j<=end;j++){

              if(HT[j].parent!=0) continue;

              if(HT[j].weight<min1){

                     min2=min1;

                     min1=HT[j].weight;

                     *s2=*s1;

                     *s1=j;

              }

              //如果 min1<=HT[i].weight<=min2,则 将HT[j].weight的值赋给min2

              else if(HT[j].weight>=min1&&HT[j].weight<min2){

                     min2=HT[j].weight;

                     *s2=j;

              }    

             

       }

}

void CreateHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int n){

       //得到哈夫曼编码

       int start,c,f;

       HC=new char*[n+1];      //下表从1开始，分配存储n个字符编码的编码表空间

       char* cd=new char[n];  //临时存放每个字符编码的动态数组空间

        cd[n-1]='\0';        //编码结束符

       for(int i=1;i<=n;i++){    //逐个字符求哈夫曼编码

              start=n-1;            //start开始指向最后，即编码结束符的位置

              c=i;f=HT[i].parent;   //f指向结点c的双亲结点,

              while(f!=0){         

                     start--;           //回溯一次，start位置向前指一个位置

                     if(HT[f].lchild==c) cd[start]='0'; //如果结点c是f的左孩子，则生成代码0

                     else cd[start]='1';                //如果结点c是f的右孩子，则生成代码0

                     c=f;f=HT[f].parent;                //继续向上回溯，直至 f的双亲为0回溯结束

              }  

              /* 注意：1.for循环是为了逐个字符求哈夫曼编码；while循环是为了对所求字符进行回溯，直至双亲为0

                       2.结点的双亲，左孩子，右孩子指向的全都是结点i，并不是结点的权值，这一点很容易混淆

              */                                   

              HC[i]=new char[n-start];    // 为第i个字符进行编码

              strcpy(HC[i],&cd[start]);   //为第i个字符编码分配空间

       }

       delete cd;                    //释放临时空间

}

int main(){

       HuffmanTree HT;

       HuffmanCode HC;

       cout<<"个字符集的频率为:"<<endl;

       CreateHuffmanTree(HT,5);

       CreateHuffmanCode(HT,HC,8);

       cout << "字符集编号" << endl;

       for (int i = 1; i <= 8; i++) {

              cout << HC[i] << endl;

       }

       return 0;}

【扩展功能】

从键盘上分别输入哈夫曼编码字符的个数以及每个字符对应的权值，程序执行中请一步一步依次显示出哈夫曼树的构造过程，最后输出每个权值对应的哈夫曼编码。

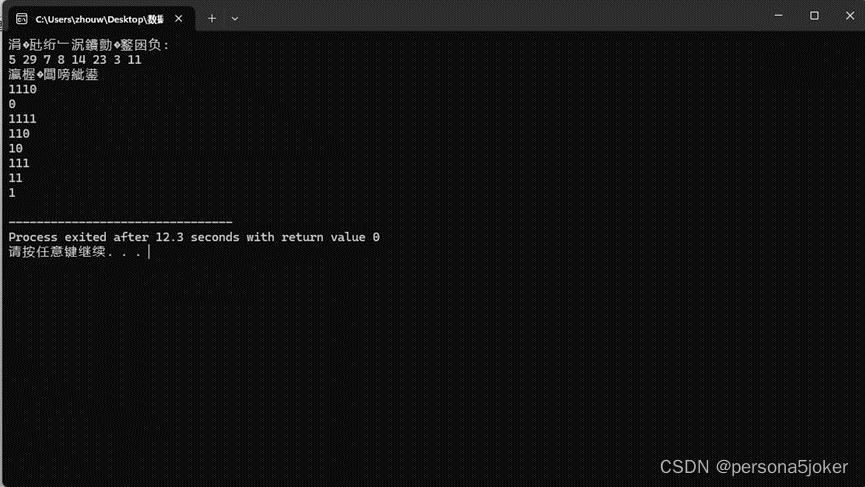
四、实验结果（写出运行程序后的结果截图）

---

---

我的其他专栏：

单片机原理

模式识别原理

数字电子技术实验

自动控制原理

模拟电子技术

数据结构

 

关注我了解更多