1.邻接矩阵

邻接矩阵采用顺序存储结构，用二维数组表示。

（1）无向图

无向图中数组array中元素表示两个顶点之间的关系，如果array[ i ] [ j ]=1表示顶点 i 和顶点 j 之间有一条边。如果为0，表示没有边将顶点 i 和顶点 j 相连。

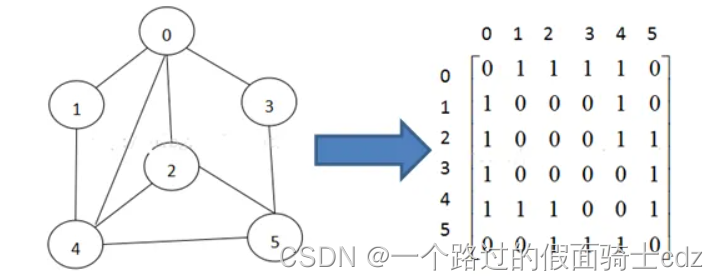观察矩阵是对称矩阵，可以压缩为n（n-1）/2的一维数组表示。

且第i行或者第i列中非零元素个数表示顶点i的度。

（2）有向图

有向图中数组array中元素表示两个顶点之间的关系，如果array[ i ] [ j ]=1表示顶点 i 到顶点 j 之间有一条边。如果为0，表示顶点 i 到顶点 j 没有边。

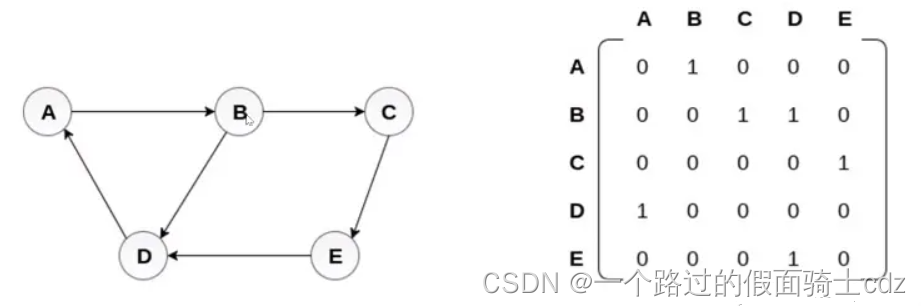
观察到矩阵不一定是对称的。

且第 i 行是顶点 i 的出度，第 i 列是顶点 i 的入度。

（3）网的邻接矩阵

网即是有权值的图。

网中数组array中元素表示两个顶点之间的关系。

如果array[ i ] [ j ]=weight表示顶点 i 到（和）顶点 j 之间有一条边，其权值为weight。

如果array[ i ] [ j ]=正无穷表示顶点 i 到（和）顶点 j 之间没有边。

如果i和j是同一顶点，array[ i ] [ j ]=0。当然也可以为正无穷，灵活变化。

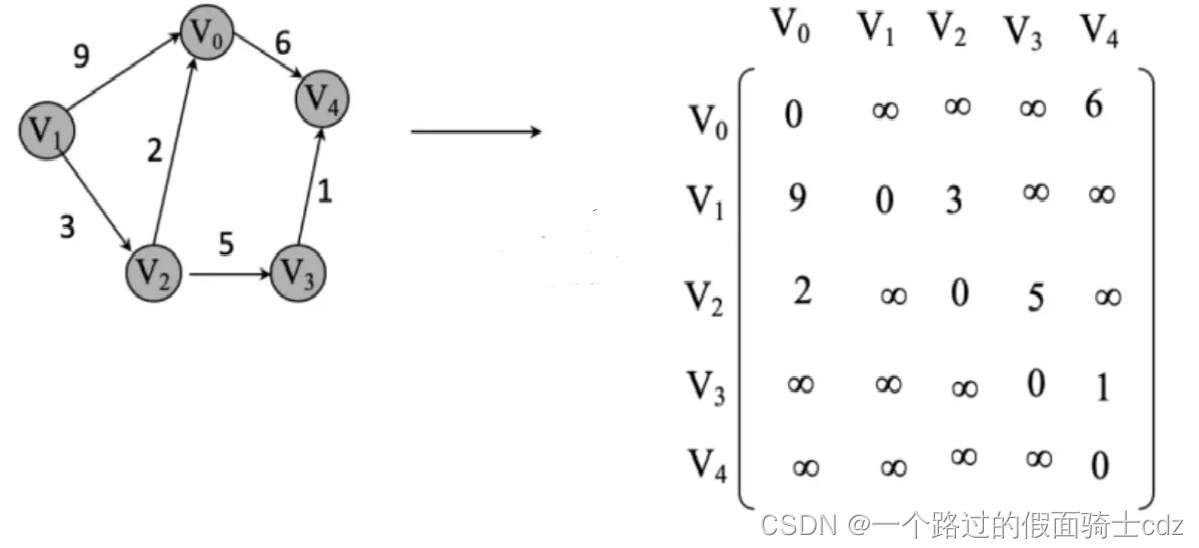
特点

1.图的邻接表示是惟一的。

2.含有n个顶点，其邻接矩阵的空间代价为O（n)，与图顶点有关，而与边无关。

3.当邻接矩阵是稀疏矩阵，可以用三元组形式存储。

#pragma once
template<class e_type>
class adjacency_matrix
{
	e_type** matrix;//表示边组
	int dot_sum;//表示顶点个数
public:
	adjacency_matrix(int init_size);
	~adjacency_matrix();
	void change(int i, int j,const e_type& data);
	bool search(int i, int j)const;
	bool add(int i, int j, const e_type& data);
	bool remove(int i, int j);
};
template<class e_type>
adjacency_matrix<e_type>::adjacency_matrix(int init_size)
{
	dot_sum = init_size;
	//申请内存空间，我不想用vector数组，腻了。
	matrix = new e_type * [dot_sum];
	for (int i = 0; i < dot_sum; i++)
		matrix[i] = new e_type[dot_sum];
	//输入边情况
	for (int i = 0; i < dot_sum; i++)
	{
		for (int j = 0; j < dot_sum; j++)
		{
			e_type temp;
			cin >> temp;
			change(i, j, temp);
		}
	}
}
template<class e_type>
adjacency_matrix<e_type>::~adjacency_matrix()
{
	for (int i = 0; i < dot_sum; i++)
	{
		e_type* temp = matrix[i];
		delete[] temp;
	}
}
template<class e_type>
void adjacency_matrix<e_type>::change(int i, int j, const e_type& data)
{
	if (i < 0 || j < 0 || i >= dot_sum || j >= dot_sum)
		throw("out of range!");
	if (search(matrix[i][j]))//有边才能修改
		matrix[i][j] = data;
	else throw("no edge");
}
template<class e_type>
bool adjacency_matrix<e_type>::search(int i, int j)const
{
	if (i < 0 || j < 0 || i >= dot_sum || j >= dot_sum)
		throw("out of range!");
	return matrix[i][j] != 0;
}
template<class e_type>
bool adjacency_matrix<e_type>::add(int i, int j, const e_type& data)
{
	if (i < 0 || j < 0 || i >= dot_sum || j >= dot_sum)
		throw("out of range");
	if (!search(i, j))//不存在才能添加
		matrix[i][j] = data;
	else throw("edge has existed!");
}
template<class e_type>
bool adjacency_matrix<e_type>::remove(int i, int j)
{
	if (i < 0 || j < 0 || i >= dot_sum || j >= dot_sum)
		throw("out of range");
	if (search(i, j))//存在才能删除
		matrix[i][j] = 0;
    //无向图
    //if (search(j, i))//存在才能删除
		//matrix[j][i] = 0;
	else throw("edge has not exist!");
}

2.邻接表

邻接表是顺序存储和链式存储相结合的一种方法。对顶点顺序存储，对其边链式存储。

顶点结点结构中数据域表示一个顶点，其指针域表示与其相关的顶点集合。

如果是网，多加一个数据项存储权值。

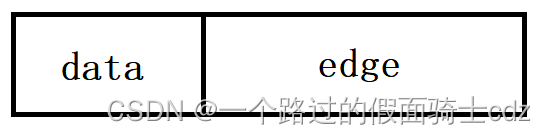
边结点结构数据域表示一个顶点，其指针指向下一个与顶点结点相关的边结点。

（1）无向图

无向图的边结点表示与顶点结点有边相连的关系。

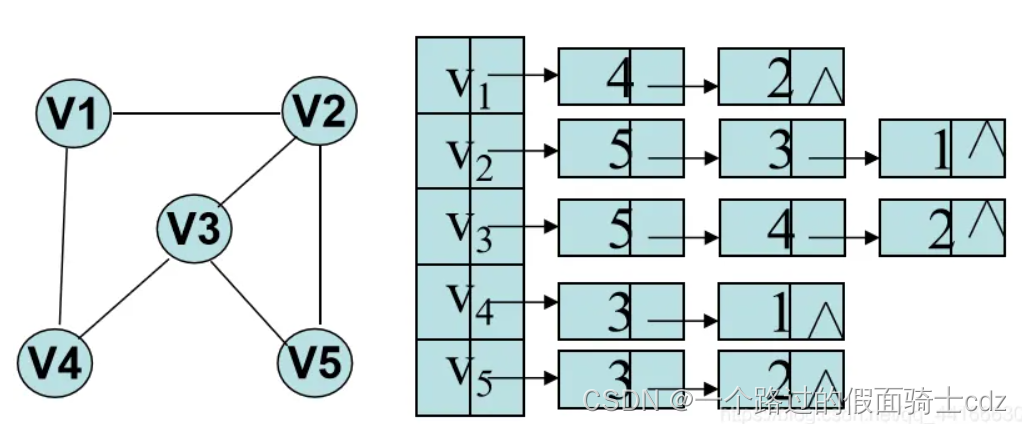
（2）有向图

有向图的边结点表示顶点结点为起点，有以边结点为终点的关系。

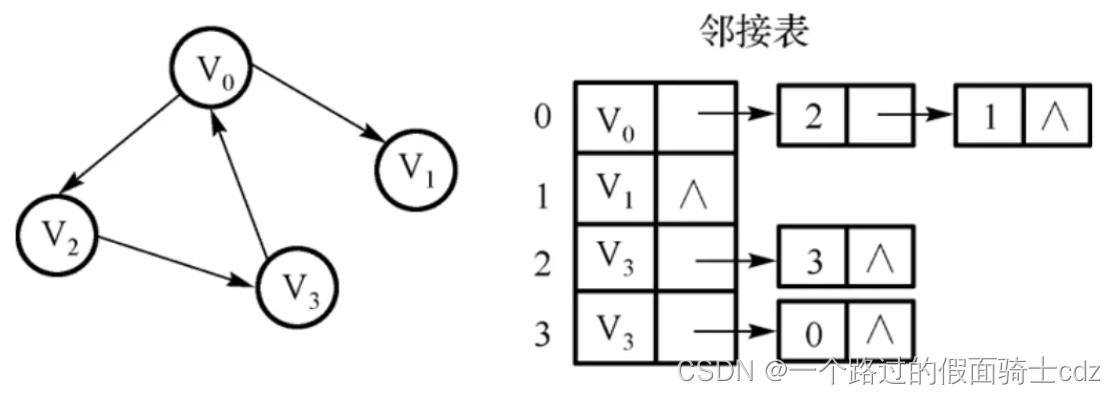
特点

1.图的邻接表表示不为1（链表前后元素可以调换）。

2.对于无向图，顶点的度是链表的长度-1。

3.对于有向图，顶点的出度是链表的长度-1。入度需要遍历整个邻接表。

4.存储空间主要与顶点数n和边数e有关，无向图空间复杂度为O（n+2e），有向图为O（n+e）。

5.当边数小于n（n-1）/2即有向图最多边数的一半时，就可以用三元组压缩存储。

//头文件
#pragma once
class adjacency_list
{
	struct edge_node
	{
		int vertex;
		edge_node* next;
		edge_node(edge_node* h = nullptr) :next(h) {}
	};
	struct vertex_node
	{
		int vertex;
		edge_node* head;
		//int weight//可以加权
		vertex_node(edge_node* h=nullptr):head(h){}
	};
public:
	vertex_node* node;
	int cur_size;
	adjacency_list(int init_size);
	~adjacency_list();
	bool search(int i, int j)const;
	bool add(int i, int j);
	bool remove(int i, int j);
};
//源文件
#include "adjacency_list.h"
adjacency_list::adjacency_list(int init_size)
{
	if (init_size <= 0)
		throw("error");
	cur_size = init_size;
	node = new vertex_node[cur_size];
}
adjacency_list::~adjacency_list()
{
	for (int i = 0; i < cur_size; i++)
	{
		while (node[i].head->next)
		{
			edge_node* p = node[i].head->next;
			node[i].head->next = p->next;
			delete p;
		}
	}
	delete[]node;
}
bool adjacency_list::search(int i, int j)const
{
	if (i < 0 || j < 0 || i >= cur_size || j >= cur_size)
		throw("out of range");
	edge_node* p = node[i].head->next;
	while (p)
	{
		if (p->vertex == j)
			return true;
		else p = p->next;
	}
	return false;
}
bool adjacency_list::add(int i, int j)
{
	if (i < 0 || j < 0 || i >= cur_size || j >= cur_size)
		throw("out of range");
	if (search(i, j))//已经存在
		return false;
	edge_node* p = new edge_node;
	p->vertex = j;
	edge_node* q = node[i].head->next;
	node[i].head->next = p;
	p->next = q;
	return true;
}
bool adjacency_list::remove(int i, int j)
{
	if (i < 0 || j < 0 || i >= cur_size || j >= cur_size)
		throw("out of range");
	edge_node* p = node[i].head->next;
	edge_node* p_pre = node[i].head;
	while (p)
	{
		if (p->vertex == j)
		{
			p_pre->next = p->next;
			delete p;
			return true;
		}
		else
		{
			p_pre = p;
			p = p->next;
		}	
	}
	return false;
}

3.十字链表

十字链表用于有向图，既可以快速查找入度边，也可以快速查出度边。

顶点结构有数据域表示顶点，指针分别表示入边表和出边表。

边结点结构 ：

 

这样，十字链表结构类似于下图：

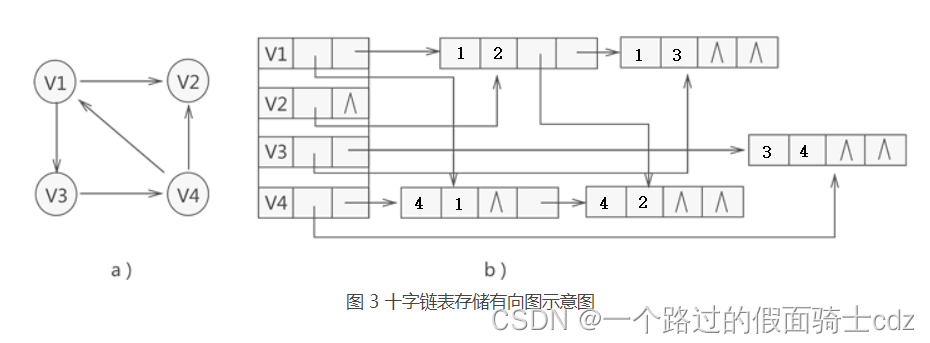
空间复杂度为O（n+e）。

 4.邻接多重表

邻接多重表适用于无向图，其相较于邻接矩阵作用是不用对一条边存储两次。

顶点结构如下：

边表结构，vexi表示顶点i，vexj表示顶点j，说明存在i和j之间相连的一条边。

linki是与i相连的下一条边，linkj是与j相连的下一条边。

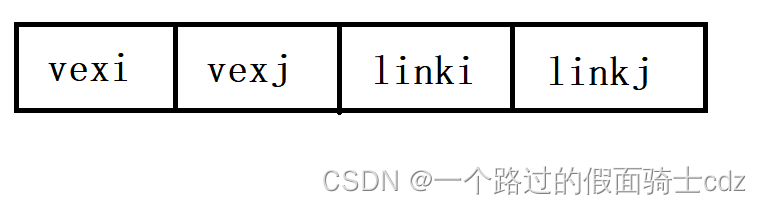
 因此，多重链表结构类似于下图：

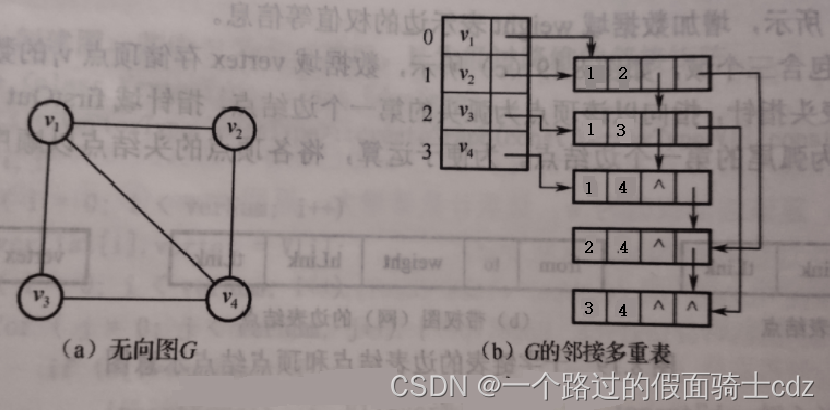
空间复杂度为O（n+e）。