(C语言 C++) 数据结构:图的实现,深度/广度优先搜索遍历,Dijkstra最短路径
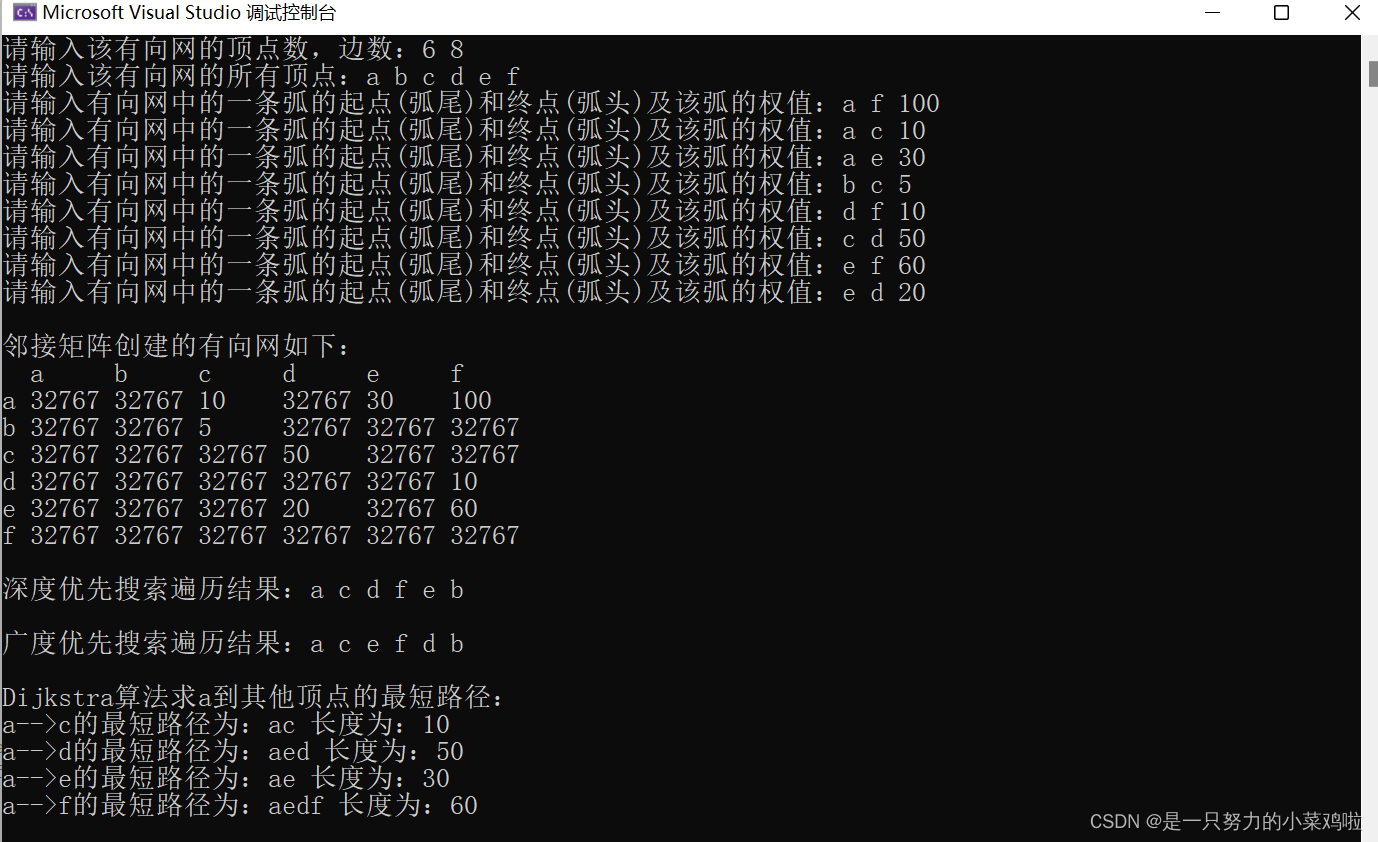
运行结果:
·
//邻接矩阵建立图
#include <iostream>
#include <iomanip>
#include <algorithm>
#include "Queue.h"
using namespace std;
#define MVNum 100 //最大顶点数
#define MAXInt 32767 //表示极大值
typedef char VerTexType; //顶点的类型
typedef int ArcType; //边的类型
typedef struct
{
VerTexType vexs[MVNum]; //顶点表
ArcType arcs[MVNum][MVNum]; //邻接矩阵
int vexNum, arcNum; //vexNum->顶点个数 arcNum->边的个数
} AMGraph;
//确定某个顶点在顶点表中的位置
int LocateVex(AMGraph &G, VerTexType v)
{
for (int i = 0; i < G.vexNum; i ++ )
if (G.vexs[i] == v)
return i;
return -1; //没有在顶点表中找到顶点v
}
//邻接矩阵创建有向网
void CreateUDN(AMGraph& G)
{
cout << "请输入该有向网的顶点数,边数:"; //6 8
cin >> G.vexNum >> G.arcNum;
//初始化顶点表
cout << "请输入该有向网的所有顶点:"; //a b c d e f
for (int i = 0; i < G.vexNum; i++) cin >> G.vexs[i];
//初始化邻接矩阵
for (int i = 0; i < G.vexNum; i++)
for (int j = 0; j < G.vexNum; j++)
G.arcs[i][j] = MAXInt;
//邻接矩阵构建有向网
for (int k = 0; k < G.arcNum; k++)
{
VerTexType v1, v2;
int weight;
cout << "请输入有向网中的一条弧的起点(弧尾)和终点(弧头)及该弧的权值:";
cin >> v1 >> v2 >> weight;
int i = LocateVex(G, v1);
int j = LocateVex(G, v2);
G.arcs[i][j] = weight;
}
}
//visited数组判断图中某个顶点是否被访问过
int *visited;
//深度优先搜索遍历连通图
void DFS(AMGraph &G, int vIndex)
{
cout << G.vexs[vIndex] << " ";
visited[vIndex] = 1;
for (int j = 0; j < G.vexNum; j++)
if (G.arcs[vIndex][j] < MAXInt && !visited[j])
DFS(G, j);
}
//深度优先搜索遍历非连通图
void DFSTraverse(AMGraph& G)
{
//选择没有被访问过的顶点进行DFS
for (int v = 0; v < G.vexNum; v++)
if (!visited[v])
DFS(G, v);
}
//广度优先搜索遍历连通图
void BFS(AMGraph& G, int vIndex)
{
Queue Q;
InitQueue(Q);
EnQueue(Q, vIndex);
cout << G.vexs[vIndex] << " ";
visited[vIndex] = 1;
while (!QueueEmpty(Q))
{
DeQueue(Q, vIndex);
for (int i = 0; i < G.vexNum; i++)
{
if (G.arcs[vIndex][i] < MAXInt && !visited[i])
{
EnQueue(Q, i);
cout << G.vexs[i] << " ";
visited[i] = 1;
}
}
}
}
//广度优先搜索遍历非连通图
void BFSTraverse(AMGraph& G)
{
//初始化visited,初始状态下所有顶点都还未被访问
visited = new int[G.vexNum];
for (int i = 0; i < G.vexNum; i ++ ) visited[i] = 0;
//若某个顶点没有被遍历过,则从这个顶点开始BFS
for (int v = 0; v < G.vexNum; v ++ )
if (!visited[v])
BFS(G, v);
}
//Dijkstra算法求最短路径, 求v0到其他顶点的最短路径
void ShortestPath_DIJ(AMGraph G, int v0)
{
int n = G.vexNum;
bool *S = new bool[n]; //S判断当前顶点是否加入顶点集
int *D = new int[n]; //D存放v0到v的最短路径
int *Path = new int[n]; //Path存放某个顶点在最短路径中的前驱
//初始化S, D, Path
for (int v = 0; v < n; v++)
{
S[v] = false;
D[v] = G.arcs[v0][v];
Path[v] = D[v] < MAXInt ? v0 : -1;
}
//将v0加入顶点集,并将v0到自身的权值置为0
S[v0] = true;
D[v0] = 0;
//每次循环确定一个顶点加入顶点集,还剩n-1个顶点要加入顶点集,所以要循环n-1次
for (int i = 1; i <= n - 1; i++)
{
int min = MAXInt;
int v = -1; //存放路径最短的顶点下标
for (int w = 0; w < n; w++)
{
//!S[w]排除顶点是自身的情况
if (!S[w] && D[w] < min)
{
v = w;
min = D[v];
}
}
if (v > -1) S[v] = true;
//判断随着路径最短的顶点v的加入,v0到其余顶点的路径长度是否发生改变,若改变,则更新
for (int w = 0; w < n; w++)
{
if (!S[w] && v != -1 && D[v] + G.arcs[v][w] < D[w])
{
D[w] = D[v] + G.arcs[v][w];
Path[w] = v;
}
}
}
//输出a到其他顶点的最短路径
for (int v = 1; v < n; v++)
{
if (S[v])
{
int pre = Path[v];
string path = "";
path += G.vexs[v];
while (pre != -1)
{
path += G.vexs[pre];
pre = Path[pre];
}
reverse(path.begin(), path.end());
cout << G.vexs[v0] << "-->" << G.vexs[v] << "的最短路径为:" << path << " 长度为:" << D[v] << endl;
}
}
delete[] S;
delete[] D;
delete[] Path;
}
int main()
{
AMGraph G;
CreateUDN(G);
cout << endl << "邻接矩阵创建的有向网如下:" << endl;
//6 8 a b c d e f a f 100 a c 10 a e 30 b c 5 d f 10 c d 50 e f 60 e d 20
for (int i = -1; i < G.vexNum; i++)
{
if (i == -1)
{
for (int j = -1; j < G.vexNum; j ++ )
if (j == -1) cout << " ";
else cout << left << setw(6) << G .vexs[j];
cout << endl;
}
else
{
for (int j = -1; j < G.vexNum; j ++ )
if (j == -1) cout << G.vexs[i] << " ";
else cout << left << setw(6) << G.arcs[i][j];
cout << endl;
}
}
cout << endl;
//初始化visited,初始状态下所有顶点都还未被访问
visited = new int[G.vexNum];
for (int i = 0; i < G.vexNum; i ++ ) visited[i] = 0;
cout << "深度优先搜索遍历结果:";
DFSTraverse(G);
cout << endl << endl;
cout << "广度优先搜索遍历结果:";
BFSTraverse(G);
cout << endl << endl;
cout << "Dijkstra算法求a到其他顶点的最短路径:" << endl;
ShortestPath_DIJ(G, 0);
return 0;
}
## Queue.h
#pragma once
#ifndef _QUEUE_H
#define _QUEUE_H
#define MAXISZE 100
#define ERROR 0
#define OK 1
using Status = bool;
struct Queue
{
int *base;
int front, rear;
};
//初始化
void InitQueue(Queue& Q);
//入队
Status EnQueue(Queue& Q, int vIndex);
//出队
Status DeQueue(Queue& Q, int& vIndex);
//判断队列为空
bool QueueEmpty(Queue& Q);
#endif // !_QUEUE_H
## Queue.cpp
#include "Queue.h"
//初始化
void InitQueue(Queue& Q)
{
Q.base = new int[MAXISZE];
Q.front = Q.rear = 0;
}
//入队
Status EnQueue(Queue& Q, int vIndex)
{
if ((Q.rear + 1) % MAXISZE == Q.front) return ERROR; //队满
Q.base[Q.rear] = vIndex;
Q.rear = (Q.rear + 1) % MAXISZE;
return OK;
}
//出队
Status DeQueue(Queue& Q, int& vIndex)
{
if (QueueEmpty(Q)) return ERROR; //队空
vIndex = Q.base[Q.front];
Q.front = (Q.front + 1) % MAXISZE;
return OK;
}
//判断队列为空
bool QueueEmpty(Queue& Q)
{
return Q.front == Q.rear;
}
运行结果:

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)