图

图的两种存储结构

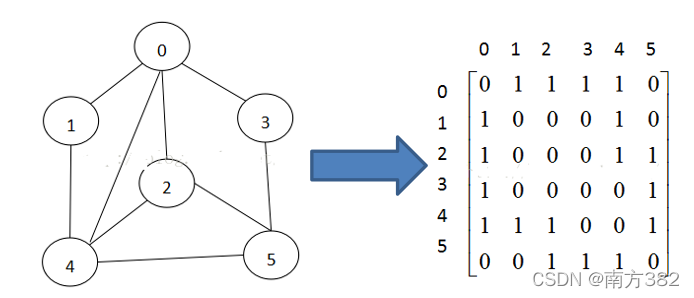
图的表示方式有两种：二维数组表示（邻接矩阵）；链表表示（邻接表）。

邻接矩阵

邻接矩阵是表示图形中顶点之间相邻关系的矩阵，n个顶点的图而言，矩阵是的row和col表示的是1....n个点。

邻接表

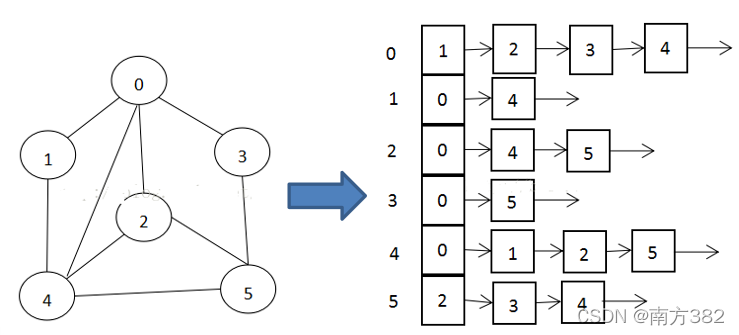
邻接矩阵需要为每个顶点都分配n个边的空间，其实有很多边都是不存在,会造成空间的一定损失.
邻接表的实现只关心存在的边，不关心不存在的边。因此没有空间浪费，邻接表由数组+链表组成

构建基本参数：

#define MAXV 50
#define INF 32767
typedef char InfoType;
typedef struct{
	int no;
	InfoType info;
}VertexType;
typedef struct {
	int edges[MAXV][MAXV];
	int n,e;
	VertexType vexs[MAXV];
}MatGraph;
typedef struct ANode{
	int adjvex;
	struct ANode*nextarc;
	int weight;
}ArcNode;
typedef struct Vnode{
	InfoType info;
	ArcNode*firstarc;
}VNode;
typedef struct {
	VNode adjlist[MAXV];
	int n,e;
}AdjGraph;

构建邻接矩阵

void CreateMat(MatGraph& g, int A[MAXV][MAXV], int n, int e)
{
	int i, j;
	g.n = n;
	g.e = e;
	for (i = 0; i < g.n; i++)
		for (j = 0; j < g.n; j++)
			g.edges[i][j] = A[i][j];
}

展示邻接矩阵

void DispMat(MatGraph g)
{
	int i, j;
	for (i = 0; i < g.n; i++) {
		for (j = 0; j < g.n; j++) {
			if (g.edges[i][j] != INF)
				printf("%4d", g.edges[i][j]);
			else
				printf("%4s", "∞");
		}	printf("\n");
	}
}

构建邻接表

void CreateAdj(AdjGraph*&G,int A[MAXV][MAXV],int n,int e){
	int i,j;ArcNode*p;
	G=(AdjGraph*)malloc(sizeof(AdjGraph));
	for(int i=0;i<n;i++){
		G->adjlist[i].firstarc=NULL;
	}
	for(int i=0;i<n;i++){
		for(int j=n-1;j>=0;j--){
			if(A[i][j]!=0&&A[i][j]!=INF){
				p=(ArcNode*)malloc(sizeof(ArcNode));
				p->adjvex=j;
				p->weight=A[i][j];
				p->nextarc=G->adjlist[i].firstarc;
				G->adjlist[i].firstarc=p;
			}
		}
	}
	G->n=n;G->e=e;
}

展示邻接表

void DispAdj(AdjGraph*G){
	int i;ArcNode*p;
	for(int i=0;i<G->n;i++){
		p=G->adjlist[i].firstarc;
		printf("%3d: ",i);
		while(p!=NULL){
			printf("%3d[%d]→",p->adjvex,p->weight);
			p=p->nextarc;
		}
		printf("∧\n");
	}
}

主函数

int main(){
	MatGraph g;
	AdjGraph* G;
	int A[MAXV][MAXV] = {
		{0,5,INF,7,INF,INF},      {INF,0,4,INF,INF,INF},
		{8,INF,0,INF,INF,9},      {INF,INF,5,0,INF,6},
		{INF,INF,INF,5,0,INF},     {3,INF,INF,INF,1,0} };
	int n = 6, e = 10;
	CreateMat(g, A, n, e);
	
	printf("(1)图的邻接矩阵：\n"); DispMat(g);
	CreateAdj(G, A, n, e);
	printf("图G的邻接表 \n");
	DispAdj(G);
	return 0;
}

图的两种遍历方法

DFS深度优先遍历

void DFS(AdjGraph*G,int v){
	ArcNode*p;
	visited[v]=1;
	printf("%d",v);
	p=G->adjlist[v].firstarc;
	while(p!=NULL){
		if(visited[p->adjvex]==0){
			DFS(G,p->adjvex);
		}
		p=p->nextarc;
	}
}

深度优先遍历非递归方法

void DFS1(AdjGraph* G, int v)
{
	ArcNode* p;
	int St[MAXV];
	int top = -1, w, x, i;
	for (i = 0; i < G->n; i++)
		visited[i] = 0;
	printf("%3d", v);
	visited[v] = 1;
	top++;
	St[top] = v;
	while (top > -1)
	{
		x = St[top];
		p = G->adjlist[x].firstarc;
		while (p != NULL)
		{
			w = p->adjvex;
			if (visited[w] == 0)
			{
				printf("%3d", w);
				visited[w] = 1;
				top++;
				St[top] = w;
				break;
			}
			p = p->nextarc;
		}
		if (p == NULL)
			top--;
	}
	printf("\n");
}

BFS广度优先遍历

void BFS(AdjGraph* G, int v)
{
	ArcNode* p;
	int queue[MAXV], front = 0, rear = 0;
	int visited[MAXV];
	int w, i;
	for (i = 0; i < G->n; i++)
		visited[i] = 0;
	printf("%3d", v);
	visited[v] = 1;
	rear = (rear + 1) % MAXV;
	queue[rear] = v;
	while (front != rear)
	{
		front = (front + 1) % MAXV;
		w = queue[front];
		p = G->adjlist[w].firstarc;
		while (p != NULL)
		{
			if (visited[p->adjvex] == 0)
			{
				printf("%3d", p->adjvex);
				visited[p->adjvex] = 1;
				rear = (rear + 1) % MAXV;
				queue[rear] = p->adjvex;
			}
			p = p->nextarc;
		}
	}
	printf("\n");
}

调用过程

int main()
{
	MatGraph g;
	AdjGraph* G;
	int A[MAXV][MAXV] = {
		{0,5,INF,7,INF,INF},      {INF,0,4,INF,INF,INF},
		{8,INF,0,INF,INF,9},      {INF,INF,5,0,INF,6},
		{INF,INF,INF,5,0,INF},     {3,INF,INF,INF,1,0} };
	int n = 6, e = 10;
	CreateMat(g, A, n, e);
	
	printf("(1)图的邻接矩阵：\n"); DispMat(g);
	CreateAdj(G, A, n, e);
	printf("图G的邻接表 \n");
	DispAdj(G);
	printf("从顶点0开始的DFS(递归):\n");
	DFS(G, 0);
	printf("\n");
	printf("从顶点开始的DFS(非递归):\n");
	DFS1(G, 0);
	printf("从顶点开始的BFS:\n");
	BFS(G, 0);
	DestroyAdj(G);
	return 0;
}

判断是否是一棵树

void DFSt(AdjGraph *G,int v,int *n,int *e)
{
    ArcNode *p;
    visited[v]=1;
    (*n)++;
    p=G->adjlist[v].firstarc;
    while(p!=NULL)
    {
        (*e)++;
        if(visited[p->adjvex]==0)
            DFSt(G,p->adjvex,n,e);
        p=p->nextarc;
    }
}
int IsTree(AdjGraph *G)
{
    int vNum=0,eNum=0,i;
    for(i=0;i<G->n;i++)
        visited[i]=0;
    DFSt(G,0,&vNum,&eNum);
    if(vNum==G->n && eNum==2*(G->n-1))
        return 1;
    else
        return 0;
}