数据结构实验二二叉树的操作与实现

编写一个程序exp7-3.cpp，实现由先序序列和中序序列以及由中序序列和后序序列构造一棵二叉树的功能（二叉树种的每个结点值为单个字符），要求以括号表示和凹入表示法输出该二叉树，并用先序遍历序列“ABDEHJKLMNCFGI”和中序遍历序列“DBJHLKMNEAFCGI”以及由中序遍历序列“DBJHLKMNEAFCGI”和后序遍历序列“DJLNMKHEBFIGCA”进行验证。编写一个程序exp7-

Qq_3463289146

1924人浏览 · 2024-03-02 19:54:31

Qq_3463289146 · 2024-03-02 19:54:31 发布

实验二 二叉树的操作与实现

一、实验目的：

1、领会二叉链存储结构和掌握二叉树中的各种基本运算算法设计；

2、领会线索二叉树的构造过程以及构造二叉树的算法设计；

3、领会哈夫曼树的构造过程以及哈夫曼编码的生成过程；

4、掌握二叉树遍历算法的应用，熟练使用先序、中序、后序3种递归遍历算法进行二叉树问题的求解；

二、实验类型: 验证性/设计性

三、实验学时：4学时

四、实验教学的重点和难点：

重点：二叉树的基本操作和遍历

难点：二叉链表的操作

五、实验内容：

1、教材P247实验题1：实现二叉树的各种基本运算的算法

编写一个程序btree.cpp，实现二叉树的基本运算，并在此基础上设计一个程序exp7-1.cpp完成以下功能。

（1）由图7.33所示的二叉树创建对应的二叉链存储结构b，该二叉树的括号表示串为“A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,i)))”。

（2）输出二叉树b。

（3）输出‘H’结点的左、右孩子结点值。

（4）输出二叉树b的高度。

（5）释放二叉树b。

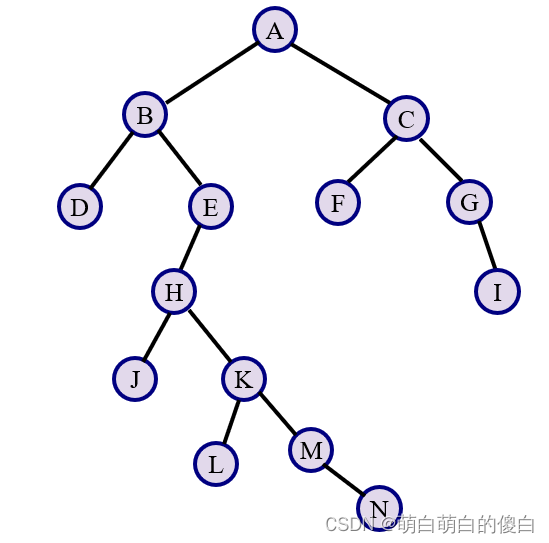
图7.33 一棵二叉树

#include<iostream>
using namespace std;
typedef char elemtype;	// 树结点的存的数据是什么类型就定义为什么类型的别名
struct Node {
	elemtype data;
	Node* lchild;
	Node* rchild;
	Node(elemtype x) :data(x), lchild(nullptr), rchild(nullptr) {}	// 带初始化的双链结点
	Node() : data(NULL), lchild(nullptr), rchild(nullptr) {}	// 重载构造函数
};
class solution {
public:
	void Create(Node*& root, string& s) {	// 创建二叉树
		Node** stack = new Node * [s.size()];	// 定义一个栈存放结点的指针
		Node* p = new Node;	// 工作指针
		int top = -1, k, j = 0;	//	k为判定左右孩子的依据
		root = nullptr;	// 树一开始只有空根
		while (s[j]) {
			switch (s[j]) {
			case '(':	// 处理lchild
				top++;
				stack[top] = p;	// 将下一个结点入栈
				k = 1;	// 左孩子
				break;
			case ')':	// 栈顶结点的子树处理完
				top--;	//将上一个结点出栈
				break;
			case',':	// 处理rchild
				k = 2;
				break;
			default:	// 存入下一个结点
				p = new Node(s[j]);	// 新建子结点
				if (root == nullptr)root = p;	// 若无根节点，则指向p
				else {
					switch (k) {
					case 1:stack[top]->lchild = p; break;	// 左孩子入栈
					case 2:stack[top]->rchild = p; break;	// 右孩子入栈
					}
				}
			}
			j++;	// 往右移动
		}
	}
	void Free(Node*& root) {	// 释放二叉树
		if (root != nullptr) {	// 为空就没法释放
			Free(root->lchild);	// 递归释放左子树
			Free(root->rchild);	// 递归释放右子树
			delete root;	//释放节点
		}
	}
	Node* Findnode(Node*& root, elemtype a) {	// 查找值为a的节点
		Node* p=new Node(NULL);	// 工作指针
		if (root == nullptr)return nullptr;	// 结点都为空了只能返回空了
		else if (root->data == a)return root;	// 找到了
		else {
			p = Findnode(root->lchild, a);	// 递归往左子树找
			if (p != nullptr)return p;	// p不指向空说明已经找到了
			else return Findnode(root->rchild, a);	// 递归往右子树找
		}
	}
	int height(Node* root) {	// 求树的深度 实际上就是f(x)=max{f(x.lchild),f(x.rchild)}+1,查最深的分支+1便是深度
		int lcheight, rcheight;
		if (root == nullptr)return 0;	// 返回0
		else {
			lcheight = height(root->lchild);
			rcheight = height(root->rchild);
			return (lcheight > rcheight) ? lcheight + 1 : rcheight + 1;
		}
	}
	void print(Node* root) {
		if (root != nullptr) {
			cout << root->data;	// 非空则输出
			if (root->lchild != nullptr || root->rchild != nullptr) {	// 存在结点便能有括号
				cout << "(";
				print(root->lchild);	// 递归左子树
				if (root->rchild != nullptr)cout << ",";	// 有右子树才输出逗号，
				print(root->rchild);	// 递归右子树
				cout << ")";
			}
		}
	}
};
int main() {
	Node* head ;	// 创建树根
	Node* q ;	// 操作指针
	solution s;	
	string str = "A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,i)))";	//	括号字符串表示的树
	s.Create(head, str);	// 创建二叉树
	cout << "输出二叉树：";
	s.print(head);	// 输出二叉树
	q = s.Findnode(head, 'H');	// q指针指向包含数据H的结点
	cout << "\nH的左孩子：" << q->lchild->data << "\tH的右孩子：" << q->rchild->data;
	cout << "\n树的深度" << s.height(head);
	s.Free(head);	// 释放树
}

2、教材P248实验题3：由遍历序列构造二叉树

#include<iostream>
#include<queue>
#include<unordered_map>
using namespace std;
typedef char Elemtype;	// 树结点的存的数据是什么类型就定义为什么类型的别名
struct Node {
	Elemtype data;
	Node* lchild;
	Node* rchild;
	Node(Elemtype x) :data(x), lchild(nullptr), rchild(nullptr) {}	// 带初始化的双链结点
	Node() : data(NULL), lchild(nullptr), rchild(nullptr) {}	// 重载构造函数
};
//输出二叉树
class solution {
public:
	void first(Node* root) {	// 先序遍历
		if (root != nullptr) {
			cout << root->data;
			first(root->lchild);
			first(root->rchild);
		}
	}
	void middle(Node* root) {	// 中序遍历
		if (root != nullptr) {
			middle(root->lchild);
			cout << root->data;
			middle(root->rchild);
		}
	}
	void last(Node* root) {		// 后序遍历
		if (root != nullptr) {
			last(root->lchild);
			last(root->rchild);
			cout << root->data;
		}
	} 
	int Nodes(Node* root) {		// 求二叉树的结点个数，分治的思想，将问题划分为子问题，再将子问题划分为更小的子问题，直到不能分为止
		if (root == nullptr)return 0;
		else return Nodes(root->lchild) + Nodes(root->rchild) + 1;	// 二叉树的节点个数：就是求每一颗数的左子树+右子树+自己
	}
	void Displeaf(Node* root) {	// 输出二叉树的叶结点
		if (root != nullptr) {
			if (root->lchild == nullptr && root->rchild == nullptr)cout << root->data;
			Displeaf(root->lchild);	// 从左往右输出树叶，若想从右往左只需调转这两句顺序
			Displeaf(root->rchild);
		}
	}
	int Lever(Node* root, Elemtype x, int h = 1) {	// 查找数据为x的结点所在深度，使用此函数时第三个参数可不填
		int l;
		if (root == nullptr)return 0;
		else if (root->data == x)return h;
		else {
			l = Lever(root->lchild, x, h + 1);	// 在左子树中找
			if (l != 0)return l;	// 说明在左子树中找到了
			else return Lever(root->rchild, x, h + 1);	// 左子树没有就往右子树找
		}
	}
	bool Like(Node* root1, Node* root2) {	// 判断两二叉树是否相似
		bool like1, like2;
		if (root1 == nullptr && root2 == nullptr)return true;
		else if (root1 == nullptr && root2 == nullptr)return false;	// 不用担心两个同为nulptr因为第一步就判断了
		else {
			like1 = Like(root1->lchild, root2->lchild);
			like2 = Like(root1->rchild, root2->rchild);
			return like1 && like2;
		}
	}
	bool Grand(Node* root, Elemtype x) {	// 查找x的所有祖先
		if (root == nullptr)return false;
		else if (root->lchild != nullptr && root->lchild->data == x || root->rchild != nullptr && root->rchild->data == x) {
			cout << root->data;
			return true;
		}
		else if (Grand(root->lchild, x) || Grand(root->rchild, x)) {
			cout << root->data;
			return true;
		}
		else return false;
	}
	Node* CreateFM(Elemtype* first, Elemtype* middle, int n) {	// 通过先序序列，中序序列来构建二叉树，n为二叉树结点个数
		Node* fm = new Node;	// 创建结点
		Elemtype* p;
		if (n <= 0)return nullptr;
		fm->data = *first;	// first中最先元素是根结点值
		for (p = middle; p < middle + n; p++)if (*p == *first)break;	//	在中序序列中找到等于*first字符的位置k，first指向根结点，找到后退出循环
		int k = p - middle;	// 确定根结点在middle中的位置
		fm->lchild = CreateFM(first + 1, middle, k);	// 递归构造左子树
		fm->rchild = CreateFM(first + k + 1, p + 1, n - k - 1);	// 递归构造右子树
		return fm;
	}
	Node* CreateML(Elemtype* last, Elemtype* middle, int n) {	// 通过后序序列，中序序列来构建二叉树，n为二叉树结点个数
		Node* ml = new Node;
		Elemtype* p;
		if (n <= 0)return nullptr;
		ml->data = *(last + n - 1);	// last中最后元素是根结点值
		for (p = middle; p < middle + n; p++)if (*p == *(last + n - 1))break;	// 在中序序列中找到等于last序列的最后字符的位置p，last指向根结点，找到后退出循环
		int k = p - middle;	// 确定根节点在middle中的位置
		ml->lchild = CreateML(last, middle, k);	// 递归构造左子树
		ml->rchild = CreateML(last + k, p + 1, n - k - 1);	// 递归构造右子树
		return ml;
	}
	void LevelOrder(Node* root) {	// 分层次的层次遍历算法
		Node* p;
		queue<Node*> q;
		int level = 1;	// 表示当前
		q.push(root);	// 根结点指针进入队列
		while (!q.empty()) {
			cout << "第" << level << "层";
			int count = q.size();	// 求当前层次的结点个数count
			for (int i = 0; i < count; i++) {
				p = q.front();	// 访问
				q.pop();	// 出队
				cout << p->data;
				if (p->lchild != nullptr)q.push(p->lchild);	// 有左孩子时进队
				if (p->rchild != nullptr)q.push(p->rchild);	// 有右孩子时进队
			}
			level++;
			cout << endl;
		}
		queue<Node*>empty;
		swap(empty, q);	// 释放q
	}
	void print1(Node* root) {	//括号表示法
		if (root != nullptr) {
			cout << root->data;	// 非空则输出
			if (root->lchild != nullptr || root->rchild != nullptr) {	// 存在结点便能有括号
				cout << "(";
				print1(root->lchild);	// 递归左子树
				if (root->rchild != nullptr)cout << ",";	// 有右子树才输出逗号，
				print1(root->rchild);	// 递归右子树
				cout << ")";
			}
		}
	}
	int height(Node* root) {	// 求树的深度 实际上就是f(x)=max{f(x.lchild),f(x.rchild)}+1,查最深的分支+1便是深度
		int lcheight, rcheight;
		if (root == nullptr)return 0;	// 返回0
		else {
			lcheight = height(root->lchild);
			rcheight = height(root->rchild);
			return (lcheight > rcheight) ? lcheight + 1 : rcheight + 1;
		}
	}
	void print2(Node* root, int height) {	// 中序凹入表示法 高度用求深度函数来完成，以递减方式表示更清晰
		if (root == nullptr)return;
		print2(root->lchild, height - 1);	// 递归左子树
		for (int i = 0; i < height; i++)cout << root->data;
		cout << endl;
		print2(root->rchild, height - 1);	// 递归右子树
	}
};

int main()
{
	Node* root;
	solution s;
	Elemtype first1[] = "ABDEHJKLMNCFGI";	// 先序序列
	Elemtype middle1[] = "DBJHLKMNEAFCGI";	// 中序序列
	string ssize1 = "DBJHLKMNEAFCGI";
	root = s.CreateFM(first1, middle1, ssize1.size());	// 由先序序列和中序序列创建二叉树
	cout << "\n由先序序列和中序序列创建的二叉树括号表示：";
	s.print1(root);	// 括号法输出
	cout << endl;
	s.print2(root,s.height(root)); // 凹入法输出   若不方便观察，深度可乘2，每次递归-2
	Elemtype middle2[] = "DJLNMKHEBFIGCA";	// 先序序列
	Elemtype last2[] = "DBJHLKMNEAFCGI ";	// 中序序列
	string ssize2 = "DBJHLKMNEAFCGI";
	root = s.CreateFM(last2, middle2, ssize2.size());	// 由后续序列和中序序列创建二叉树
	cout << "\n由后序序列和中序序列创建的二叉树括号表示：";
	s.print1(root);	// 括号法输出
	cout << endl;
	s.print2(root, s.height(root)); // 凹入法输出   若不方便观察，深度可乘2，每次递归-2
}

3、教材P248实验题5：构造哈夫曼树生成哈夫曼编码

编写一个程序exp7-5.cpp，构造一棵哈夫曼树，输出对应的哈夫曼编码和平均查找长度，并对下表（表7.8）所示的数据进行验证。

表7.8 单词及出现的频度

单词

The

and

that

for

His

are

频度

1192

677

541

518

462

450

242

195

190

181

174

157

138

124

123

#include<iostream>
using namespace std;
//struct HTNode {	// 哈夫曼树结点
//	string data;	// 结点数据
//	string huffmancode;	// 结点哈夫曼编码
//	HTNode* lchild;
//	HTNode* rchild;
//	int path;	// 路径长度
//	int weight;	//权重
//	HTNode() :data(NULL), lchild(nullptr), rchild(nullptr), path(0) {}
//};
struct HTNode {	// 哈夫曼树结点
	string data;	// 结点数据
	string huffmancode;	// 结点哈夫曼编码
	HTNode* lchild;
	HTNode* rchild;
	HTNode* parent;	// 改成别的用作标记已被用作树叶也行
	int path;	// 路径长度
	int weight;	//权重
	HTNode() :lchild(nullptr), rchild(nullptr), parent(nullptr), path(0) {}
	HTNode(string x) :data(x), lchild(nullptr), rchild(nullptr), parent(nullptr), path(0) {}
};
class solution {
public:
	HTNode* CreateHT(string s[], int weight[], int n) {	// 构造叶子结点个数为n的哈夫曼树，
		HTNode** ht = new HTNode * [2 * n - 1];	// 每个结点存放在ht数组中
		HTNode* root;
		for (int i = 0; i < n; i++) {
			ht[i] = new HTNode;
			ht[i]->data = s[i];
			ht[i]->weight = weight[i];
		}
		int lnode, rnode, min1, min2;
		for (int i = n; i < 2 * n - 1; i++) {	// 构造哈夫曼树n-1个非叶结点
			ht[i] = new HTNode;
			min1 = min2 = 0x7fffffff;	//	int类型的最大值
			lnode = rnode = -1;	// lnode和rnode指向两个权值最小的结点
			for (int k = 0; k < i; k++) {	// 每建立一个结点，需要遍历的尾部就会增加
				if (ht[k]->parent == nullptr) {
					if (ht[k]->weight < min1) {	// min1<=min2,lnode<rndoe
						min2 = min1;
						rnode = lnode;
						min1 = ht[k]->weight;
						lnode = k;
					}
					else if (ht[k]->weight < min2) {
						min2 = ht[k]->weight;
						rnode = k;
					}
				}
			}
			ht[i]->weight = ht[lnode]->weight + ht[rnode]->weight;	// ht[i]作为双亲结点
			ht[i]->lchild = ht[lnode];
			ht[lnode]->parent = ht[i];
			ht[i]->rchild = ht[rnode];
			ht[rnode]->parent = ht[i];
		}
		root = ht[2 * n - 2];
		delete[]ht;	// 释放一下
		return root;
	}
	void HFMCode(HTNode*& root, string q = "") {	// 递归给结点赋上哈夫曼编码
		if (root == nullptr)return;
		root->huffmancode = q;
		HFMCode(root->lchild, q + '0');	// 往左走哈夫曼编码是“+0”
		HFMCode(root->rchild, q + '1');	// 往右走哈夫曼编码是“+1”
	}
	void Displeaf(HTNode* root) {	// 因为是哈夫曼树，输出只用输出叶子结点的值和哈夫曼编码，这里采用从左往右输出树叶
		if (root != nullptr) {
			if (root->lchild == nullptr && root->rchild == nullptr)cout << root->data << "：" << root->huffmancode << endl;
			Displeaf(root->lchild);	// 从左往右输出树叶，若想从右往左只需调转这两句顺序
			Displeaf(root->rchild);
		}
	}
	int WPL(HTNode* root, int height=0) {	//	带权路径长度
		if (root->lchild == nullptr && root->rchild == nullptr)return root->weight * height;
		return WPL(root->lchild, height + 1) + WPL(root->rchild, height + 1);
	}
	int Sum(HTNode* root) {	//	权值之和
		if (root->lchild == nullptr && root->rchild == nullptr)return root->weight;
		return Sum(root->lchild) + Sum(root->rchild);
	}
	double ASL(HTNode* root) {	// ASL=1->n∑pi*ci ,pi查找的频率，ci比较的次数（深度），pi=weight/∑weight，再求频率有点麻烦，单个带权路径长度/WPL即pi*ci
		return (double)WPL(root) / Sum(root);
	}
};
int main() {
	int weight[] = { 1192,677,541,518,462,450,242,195,190,181,174,157,138,124,123 };
	string s[] = { "The","of","a","to","and","in","that","he","is","at","on","for","His","are","be" };
	HTNode* root;
	solution ss;
	root=ss.CreateHT(s, weight, 15);
	ss.HFMCode(root);
	ss.Displeaf(root);
	cout<<"\n平均查找长度："<<ss.ASL(root);
}

4、教材P248实验题8：简单算术表达式二叉树的构建和求值

编写一个程序exp7-8.cpp，先用二叉树来表示一个简单算术表达式，树的每一个结点包括一个运算符或运算数。在简单算术表达式中只包含+、-、*、/和一位正整数且格式正确（不包括括号），并且要按照先乘除后加减的原则构造二叉树，图7.34所示为“1+2*3-4/5”代数表达式对应的二叉树，然后由对应的二叉树计算该表达式的值。

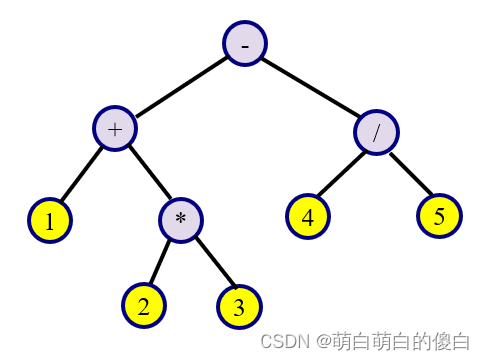
图7.34 二叉树表示简单算术表达式

#include <iostream>
#include <string>
#include <cstring>
#include <stack>
using namespace std;
#define ElemType char
typedef struct node {
    ElemType elem;
    struct node* lchild;
    struct node* rchild;
}BTNode;
void createBT(BTNode*& BT, string str) {
    stack<BTNode*> sta;
    BTNode* p;
    for (int i = 0; i < str.size(); i++) {
        p = new BTNode;
        p->lchild = NULL;
        p->rchild = NULL;
        char ch = str[i];
        if (ch == '*' || ch == '/') {
            p->elem = ch;
            BTNode* r = new BTNode;
            i++;
            r->elem = str[i];
            r->lchild = NULL;
            r->rchild = NULL;
            p->rchild = r;
            p->lchild = sta.top();
            sta.pop();
            sta.push(p);
        }
        else if (ch == '+' || ch == '-') {
            p->elem = ch;
            if (sta.size() == 2) {
                BTNode* r = sta.top();
                sta.pop();
                sta.top()->rchild = r;
            }
            p->lchild = sta.top();
            sta.pop();
            sta.push(p);
        }
        else {
            p->elem = ch;
            sta.push(p);
        }
        p = NULL;
        free(p);
    }
    if (sta.size() == 2) {
        BTNode* r = sta.top();
        sta.pop();
        sta.top()->rchild = r;
    }
    BT = sta.top();
}
int calculate(BTNode*& BT) {
    char ch = BT->elem;
    if (ch == '+') return calculate(BT->lchild) + calculate(BT->rchild);
    else if (ch == '-') return calculate(BT->lchild) - calculate(BT->rchild);
    else if (ch == '*') return calculate(BT->lchild) * calculate(BT->rchild);
    else if (ch == '/') return calculate(BT->lchild) / calculate(BT->rchild);
    else return ch - '0';
}
void displayBT(BTNode*& BT) {
    if (BT != NULL) {
        cout << BT->elem;
        displayBT(BT->lchild);
        displayBT(BT->rchild);
    }
    else {
        printf("#");
    }
}

void destroyBT(BTNode*& root) {
    if (root != NULL) {
        destroyBT(root->lchild);
        destroyBT(root->rchild);
        free(root);
    }
}
int main() {
    string str = "1+2*3-4/5";
    BTNode* BT;
    createBT(BT, str);
    cout << "简单算术表达式二叉树为：\n";
    displayBT(BT);
    cout << "\n\n该表达式的运算结果为：" << calculate(BT) << "\n\n";
    destroyBT(BT);
    system("pause");
    return 0;
}