数据结构之平衡二叉树

1 树： 由n（n>=0）个有限个节点组成的集合，该集合可以是空树或者由一个根节点及其互不相交的左右子树组成。根无前驱，有多个后继。

2 二叉树：在树的基础上，限定其后继最多为2个。

二叉树的一些性质：
性质1：
二叉树的第i层上最多有2^(i-1)个结点（i>0）。
性质2：
深度为k的二叉树最多具有2^k－1个结点。（k>0）
性质3：
对于任意一棵二叉树，如果叶子结点数为a，度数为2的结点总数为b，则有: a＝b＋1。
性质4：
具有n个结点的完全二叉树的深度k为[log2n]+1。（注：2为底数）
性质5：
在完全二叉树中，若从上至下，从左至右，则编号为i的节点，左孩子编号必为2i，右孩子编号必为2i+1；其双亲编号必为i/2（i=1时根除外）。

3 完全二叉树：除最后一层外，每层的节点数均达到最大值，在最后一层上只是缺少右边的若干个节点。

4 满二叉树：树中布满节点共2^k－1；
且每层为2^(k-1)个。

5 平衡二叉树（AVL）：二叉树的每个节点作为根节点时，它的左子树和右子树的绝对值不超过1，也叫平衡因子，只能为1、0、-1。

6 哈夫曼树：给定一组具有确定权值的叶子节点，带权路径长度最小的二叉树。

下面我们以例子来说明平衡二叉树：手动画出数组为d[10]={3,2,1,4,5,6,710,9,8};这个平衡二叉树。
首先我们要知道：数组的数据存放在二叉树中时，左子树的数比根节点小；右子树的数比根节点大。

二叉树的正常排序：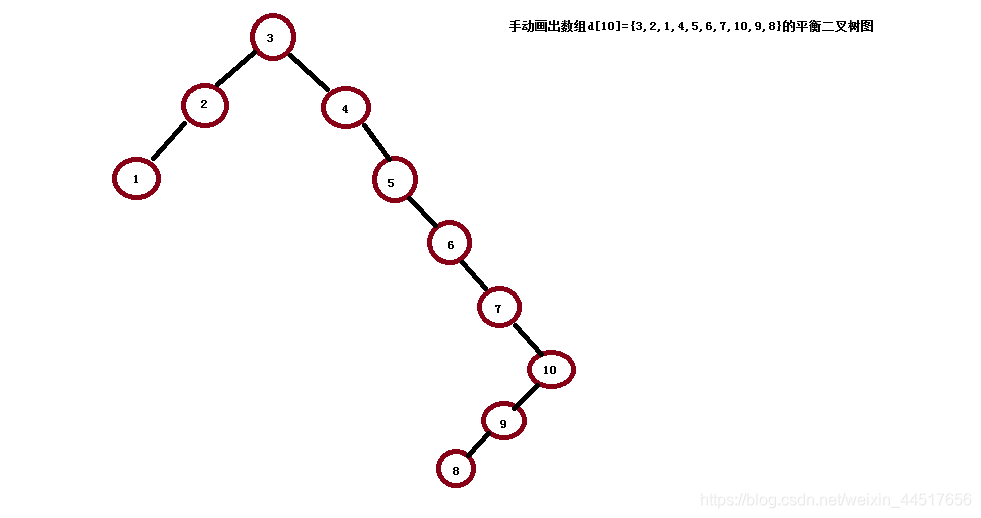

明显可以看出，如果我们要查找8的话，8大于3，往右找，8大于4，往右找……需要判断非常多次，效率低，所以我们需要改进提高效率，所以引进平衡二叉树。

1）我们利用平衡二叉树在系统存放数据时，系统会一个一个存放，当一出现不符合平衡二叉树的原理时，它会立即帮你自动旋转，符合后，再插入下一个数据节点。所以我们先存放3。

2）再插入2数据节点。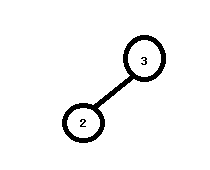

3）再插入1节点。此时我们可以看出，左子树深度为2，右子树深度为0,2-0大于1了，不符合平衡二叉树的概念，所以我们需要改变，方法是旋转。大于1说明左的长，所以需要右转。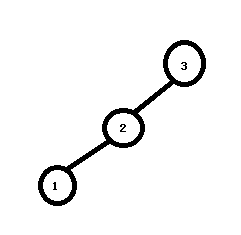

4）右转后。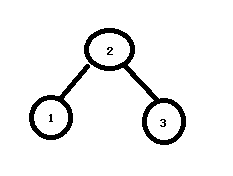

5）继续插入数据节点4。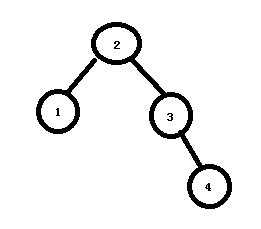

6）插入数据节点5后，可以看出2和3节点的平衡因子都是-2，负数说明右子树长，需要左转。，但是先解决3、4 、5这棵最小不平衡子树，就近原则。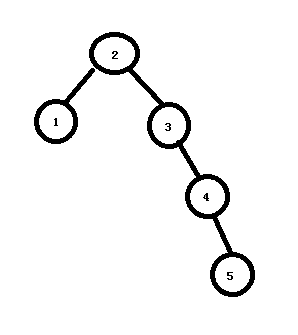

7）左转节点3后。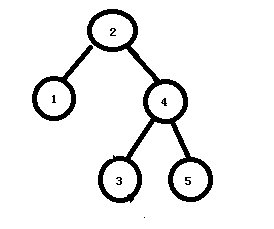

8）下面继续插入6，可以看出2的左子树深度为1；右子树深度为3；平衡因子为1-3=-2，需要左转。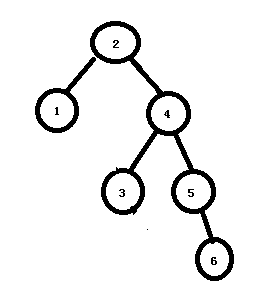

9）左转节点2后。被覆盖的节点3被当做新根节点的左子节点的右节点。即新根节点4的新左子树2的右节点；或者最简单的说变成原根节点的右子节点。不用担心3的插入是否会覆盖2原来的右子节点，因为它本身的右子节点变成了新根节点。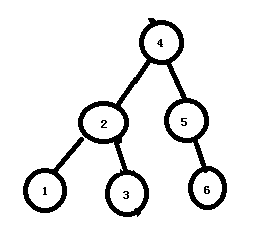

10）继续插入数据节点7。发现节点5的平衡因子为-2。需要左转。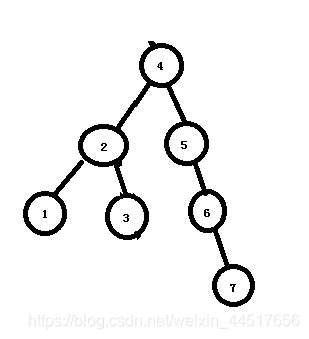

11）左转节点5后。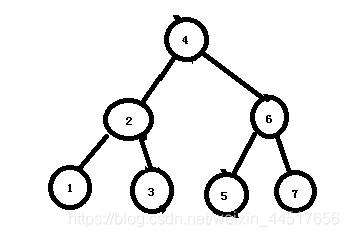

12）继续插入节点10。没有问题。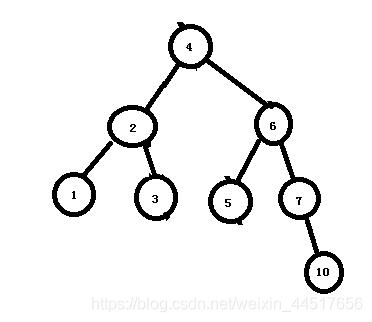

13）下面重点也是难点来了。继续插入节点9。看看出节点4、6、7平衡因子都是-2。但是这种不平衡是特殊的。如何特殊呢？我们先正常的将7左转看看。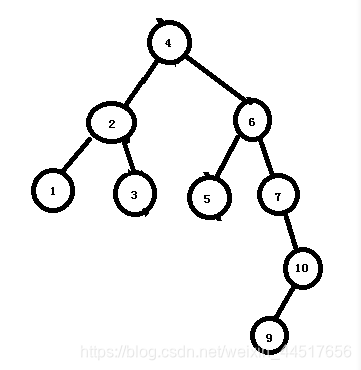

14）将节点7左转后。可以看到，这种特殊的不平衡左转后，怎么还是不平衡呢？该怎么解决呢？再右转？那不是变回原来了吗？实际上我们需要在他旋转之前做出改变。其实细心的同学已经发现，不平衡时的平衡因子要么全为负，要么全为正，那么上图的右子树节点4、 6 、7全是-2，10为什么是+1呢？所以这个改变就是将其因子改为负数。而不是下面的直接旋转。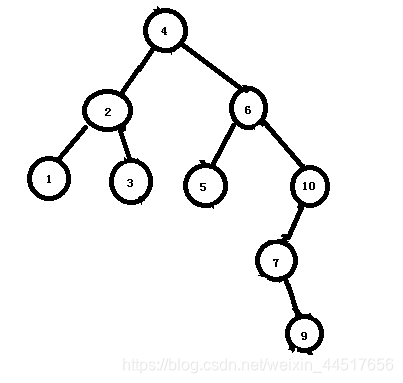

15）在旋转节点7之前，做出改变，使一边的平衡因子全为正或负数。所以我们先将节点10右转。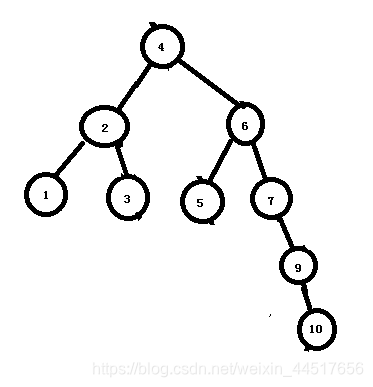

15）然后再对原来导致不平衡的节点7进行左旋转。那么就解决了上面的问题。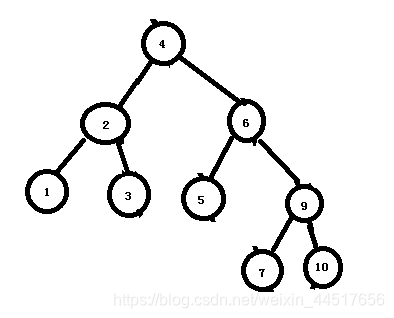

16）继续插入节点8。可以看出节点4、6平衡因子都是-2，需要对节点6左旋（改变之后即使有更近的不平衡，仍对该节点左旋，即接下来不对7，而是仍对6左旋）。但是节点9和上面一样，平衡因子为+1，所以我们需要在旋转之前做出改变，使它全为负。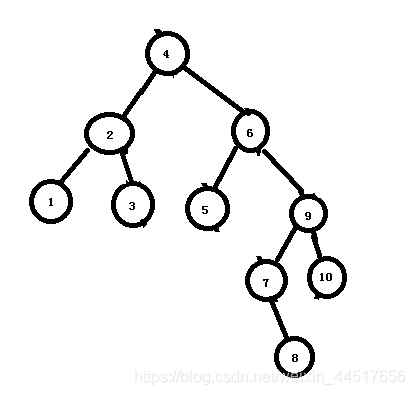

17）同样的，因为节点9的因子为+1，需要先改变。对9进行右旋，需要注意的是，新根节点7的右节点8，右旋后被新右节点9覆盖，所以他应该接入节点9的左子树。！！！即新根节点若有右节点被覆盖，则连接在新右节点的左节点中。与左旋时类似，即第8步。若左旋时，新根节点的左节点被覆盖，则连接到新左节点的右节点中。下图是改变之后。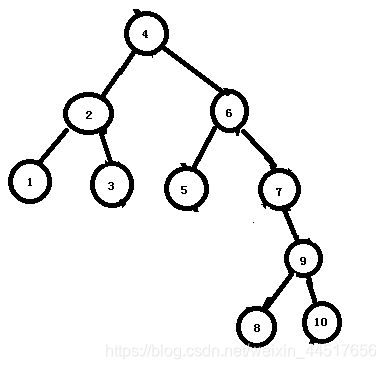

18）改变之后，可以看出，节点4 6 7是不符合平衡因子范围的，理应对节点7左转，但是对于作出改变而出现的这种最近问题，旋转的应该是没改变之前的节点，即6，这里也是需要注意的。对节点6进行左转后：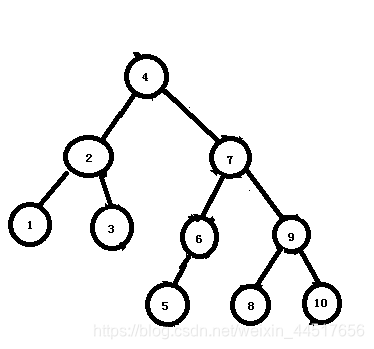

以上就是我们最终的答案，看懂了这个例题基本上你也差不多搞懂了平衡二叉树的实现原理了，给自己鼓个掌！

最后总结一些难点：
1）第8点的左旋和第16点的右旋。左旋时，新根节点的左节点被覆盖后，放在原节点的右节点中；右旋时，新根节点的右节点被覆盖后，放在原节点的左节点。
2）改变之后造成的不平衡，不应该按照就近原则先旋转，而是对做出改变之前的不平衡节点进行旋转。即第18点。

建议：看完之后一定要自己用半个小时手动画，加强练习，否则你是很容易忘掉。