前言 

本文内容源于对《数据结构（C语言版）》（第2版）和王道讲解及博主的笔记整理和总结。

可结合以下链接“食用”：

【考研】《数据结构》知识点总结.pdf_数据结构知识点总结pdf,考研数据结构知识点总结背诵-其它文档类资源-CSDN下载

一、基本概念

1、拓扑排序：可以用来判断图是否有环。（以下存储结构：邻接表）（网：带权的图）

2、有向无环图（DAG图）：一个无环的有向图。（描述一项工程或系统的进行过程的有效工具）

3、AOV-网：用顶点表示活动，用弧表示活动间的优先关系的有向图。

4、拓扑排序：AOV-网中所有顶点排成一个线性序列，该序列满足：若在AOV-网中由顶点  到顶点  有一条路径，则在该线性序列中的顶点  必定在顶点  之前。

5、对于一般的图来说，若其邻接矩阵是三角矩阵，则存在拓扑序列，反之不一定成立。

6、若一个有向图的顶点不能排在一个拓扑序列中，表示图中必有回路，该回路构成一个强连通分量，即则可判定该有向图含有顶点数目大于1的强连通分量。

7、若拓扑排序算法中为暂存入度为0的顶点，可使用栈，也可使用队列。

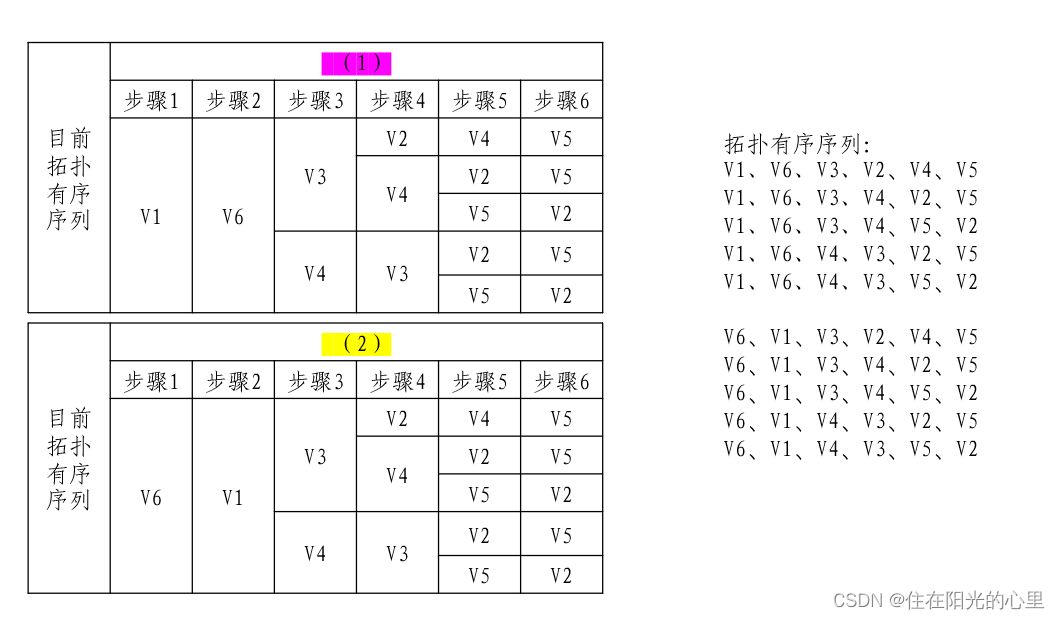
二、拓扑排序的过程

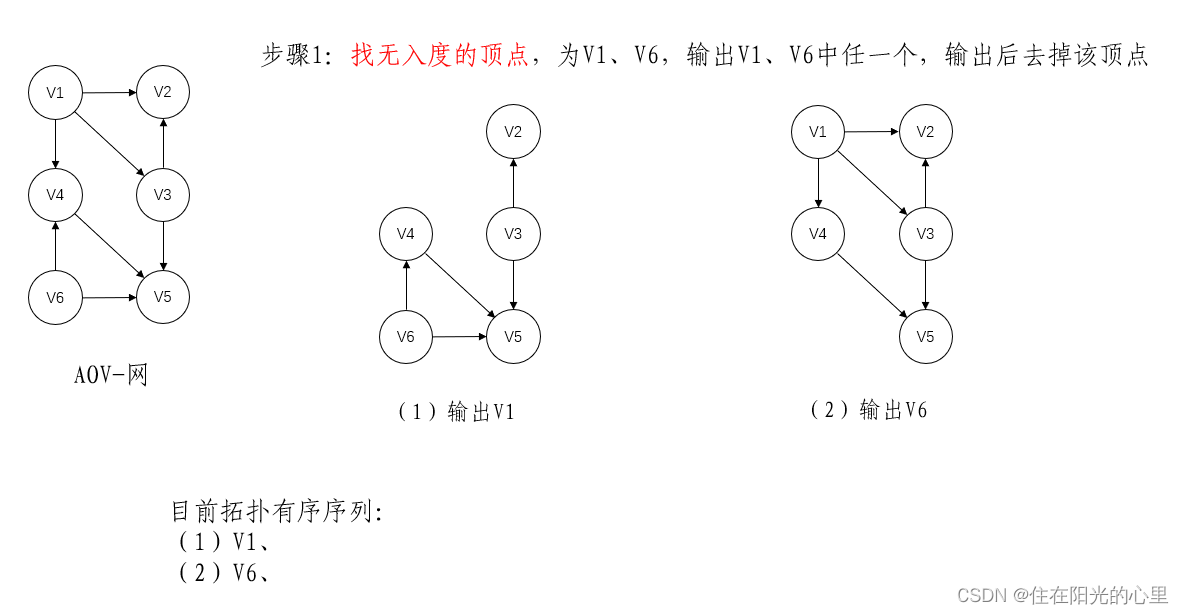
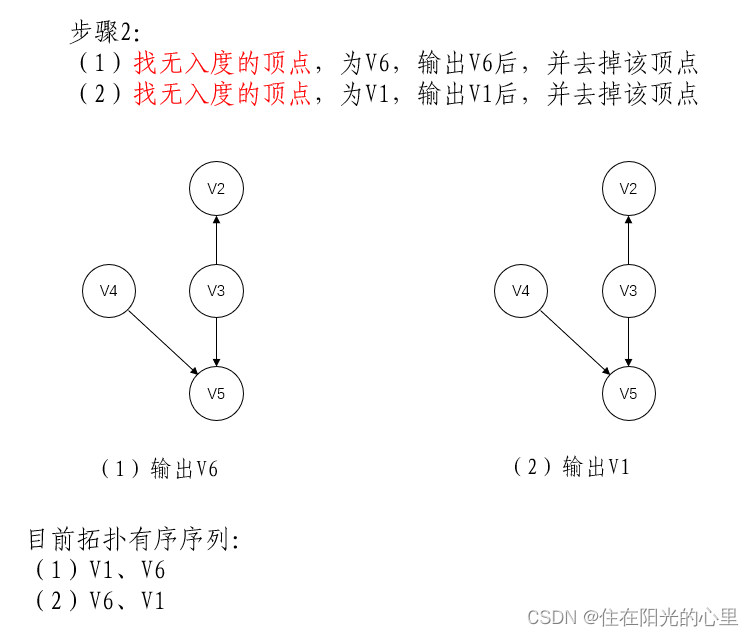
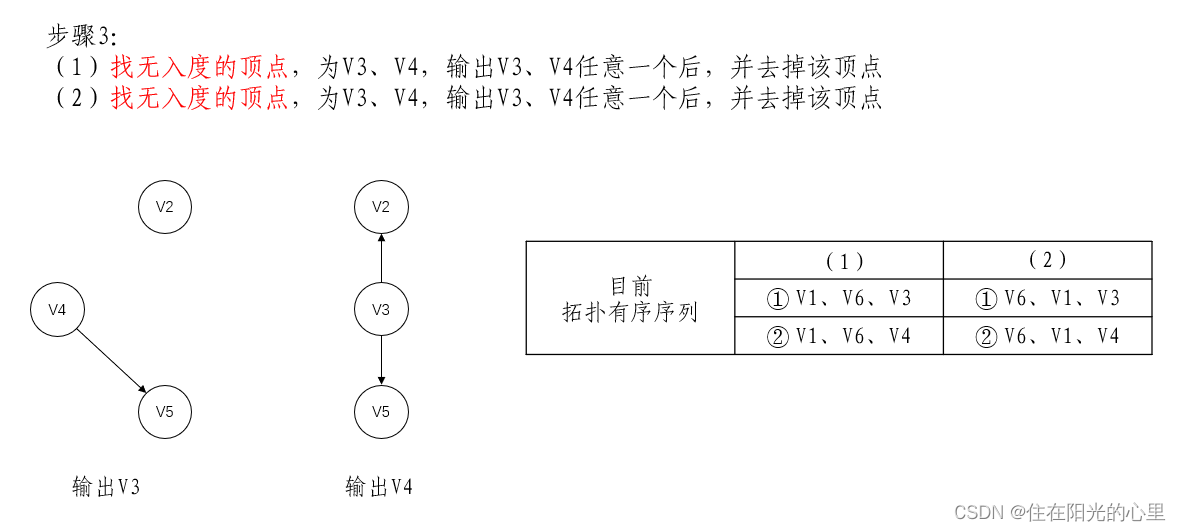
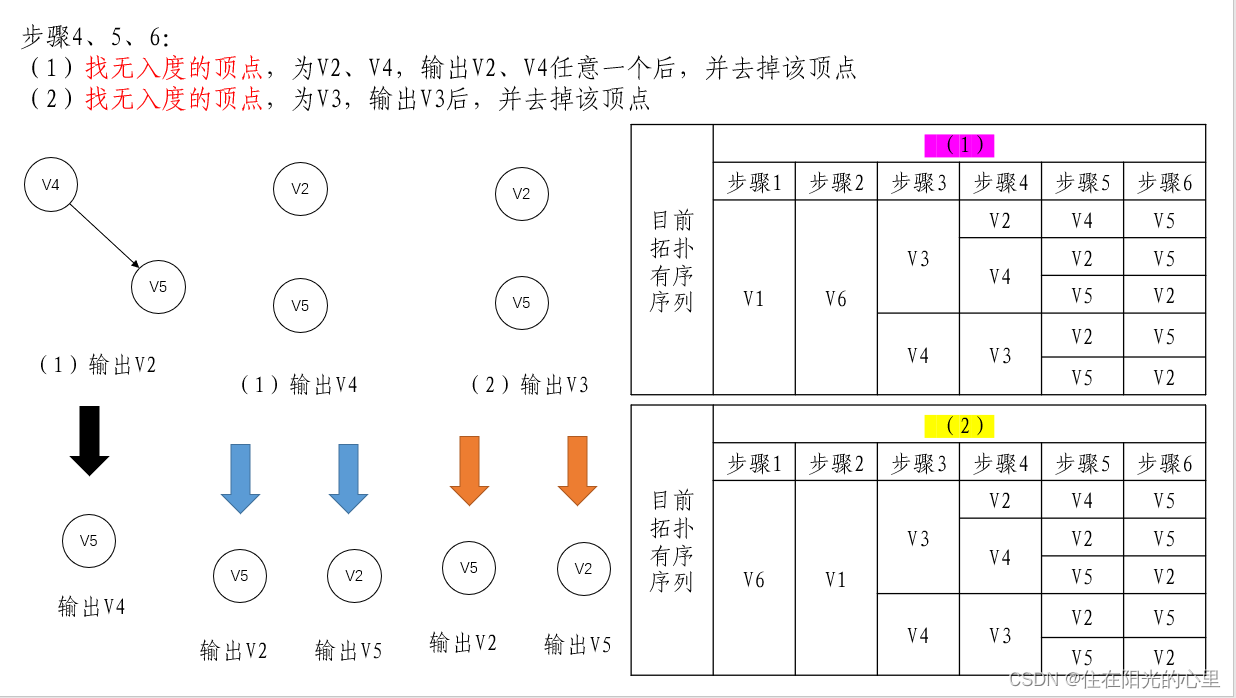
（1）在有向图中选一个无前驱的顶点且输出它。

（2）从图中删除该顶点和所有以它为尾的弧。

（3）重复（1）和（2），直至不存在无前驱的顶点。

（4）若此时输出的顶点数小于有向图中的顶点数，则说明有向图中存在环，否则输出的顶点序列即为一个拓扑序列。

三、拓扑排序的实现

引入以下辅助的数据结构：

(1) 一维数组indegree[i]：存放各顶点入度，没有前驱的顶点就是入度为零的顶点。删除顶点及以它为尾的弧的操作，可不必真正对图的存储结构进行改变，可用弧头顶点的入度减1的办法来实现。
(2) 栈S：暂存所有入度为零的顶点，这样可以避免重复扫描数组indegree检测入度为0的顶点，提高算法的效率。
(3) 一维数组topo[i]：记录拓扑序列的顶点序号。

【算法步骤】
① 求出各顶点的人度存人数组 indegree[i] 中，并将入度为0的顶点入栈。
② 只要栈不空，则重复以下操作:
● 将栈顶顶点 V 出栈并保存在拓扑序列数组 topo 中; 
● 对顶点  的每个邻接点  的入度减1，如果  的入度变为0，则将  入栈。
③ 如果输出顶点个数少于AOV-网的顶点个数，则网中存在有向环，无法进行拓扑排序，否
则拓扑排序成功。

//【算法描述】 
Status Topologica lSort (ALGraph G,int topo[] ){
// 有向图 G 采用邻接表存储结构
// 若 G 无回路，则生成 G 的一个拓扑序列 topo[] 并返回 OK， 否则 ERROR

    FindInDegree (G, indegree);   //求出各顶点的入度存人数组indegree中
    InitStack(S);    //栈 s 初始化为空
    for (i = 0; i < G.vexnum; ++i)
        if(!indegree[i])   
            Push(S, i);    //入度为0者进栈
    m = 0;   //对输出顶点计数，初始为0
    while (!StackEmpty(S)){  //栈 s 非空
        Pop(S, i);     //将栈顶顶点v(i)出栈
        topo[m] = i;    //将v(i)保存在拓扑序列数组 topo 中
        ++m;     //对输出顶点计数
        p = G.vertices[i].firstarc;    //p 指向 v(i) 的第一个邻接点
        while(p != NULL){
            k = p->adjvex;    // v(k) 为 v(i) 的邻接点
            --indegree[k];    // v(i) 的每个邻接点的入度减1
            if(indegree[k] == 0) Push(S, k);    //若入度减为0，则入栈
            p = p->nextarc;    //p 指向顶点 v(i) 下一个邻接结点
        }
    }
    if (m < G.vexnum)     //该有向图有回路
        return ERROR;
    else return OK;
}

 【算法分析】

对有 n 个顶点和 e 条边的有向图而言，

建立求各顶点入度的时间复杂度为  ；

建立零入度顶点栈的时间复杂度为 ；

在拓扑排序过程中，若有向图无环，则每个顶点进栈，出一次栈，入度减1的操作在循环中总共执行 e 次，所以，总的时间复杂度为  。