魔乐社区

重点题：

第一章：小测-2、4、7

第二章：小测-3 & 编程-2、3

 

第一章 概论

part 1: 小测验

 

 

 

 

 

答案：

1.C你选对了

解析：  A、向量：直接访问型线性结构  B、散列表：目录索引型线性结构  C、图：无序  D、队列：是线性表按操作分类的一种（先入先出）

 

2.D你选对了

解析：  A、数组：按索引值从小到大存放在一片相邻的连续区域，定义了存储结构  B、双链表：链式存储  C、顺序表：按索引值从小到大存放在一片相邻的连续区域，定义了存储结构  D、队列：可以是顺序或链式存储，是逻辑结构

 

3.A、C你选对了

解析：  A、算法保证计算结果的正确性。  B、指令必须有限  C、算法不能含有死循环，必须在有限步骤内结束  D、算法具有确定性

 

4.B、D你选对了

解析：  A、(4)当f(n)=n,g(n)=n*2, 无论a多大，g(n)都不可能是O(af(n)).  B、(2) 如果f(n)是O(g(n))，g(n)是O(h(n)), 则f(n)是O(h(n)),所以f(n)+g(n)是O(h(n))  C、(3)logan=log(n)/log(a),logbn=log(n)/log(b),所以前者与后者只差了一个常数项，所以logbn一定是O(logan)  D、(1) 根据O()定义可知.

 

5.A、B你选对了

解析：  A、本代码实际上是求a中有序子数组中最长的长度。譬如，在[1, 8, 1, 2, 5, 0, 11, 9]中，最长的是[1, 2, 5]，长度为3 。其时间复杂度与a中元素的实际取值状态相关。 1)若a的所有元素是按照降序方式排列。则外层循环n-1次，每次内层只执行一次，整个开销为θ(n) 2)若a的所有元素是按照升序方式排列。则外层循环n-1次，每次内层需要执行n-i-1次，整个开销为θ(n^2) 所以，一般来说，时间复杂度是Ω(n)的，也是O(n^2)

 

6.20

解析： 注意i从1到9全部遍历，j分别从2，4，6,...开始遍历到9，当i大于5时，循环不再对m进行操作.
i=1结束循环时，m=8；
i=2结束循环时，m=8+6=14；
i=3结束循环时，m=14+4=18；
i=4结束循环时，m=18+2=20；

7.(5)(1)(2)(4)(3)

解析： 计算复杂度时，系数是可以忽略的。(5)和(1)是指数级复杂度，大于(2)(3)(4)多项式级复杂度，区别在于指数中是否有n。而(5)的指数里还有指数级复杂度的表达式，(1)的指数是n，为多项式级，故(5)比(1)复杂。对于(2)(3)(4)，(2)的指数最大，为2.5，(4)的指数居中，为2，(3)的指数最小，解释如下：logn的任意实数次方的复杂度都小于n，故(logn)^4比n复杂度低，故n*(logn)^4比n*n复杂度低，故(4)比(3)复杂，故答案为(5)(1)(2)(4)(3) 

 

part 2: 编程题

（太简单了，略）

 

 

第二章 线性表

part 1: 小测验

 

 

答案 

1.B、C、D你选对了

解析：  A、采用链接存储，便于插入和删除操作，如果采用顺序存储，插入和删除时需要大量移动元素，参考数组的元素删除  B、采用链接存储，便于插入和删除操作  C、顺序存储是按索引值从小到大存放在一片相邻的连续区域  D、线性表采用链接存储，在结点中存储link信息，不需占用连续存储单元

 

2.A、D你选对了

解析：  A、线性表在顺序存储时，查找第i个元素的时间与i的数值无关。 因为存储空间是连续的，直接由i可以得到元素位置  B、线性表在链式存储时，查找第i个元素的时间与i的数值无关。 因为存储空间是不连续的，需要从头或者尾结点开始查找元素，i越大，时间越长，时间不可能与i无关  C、线性表在顺序存储时，查找第i个元素的时间与i的数值成正比。 因为存储空间是连续的，直接由i可以得到元素位置  D、线性表在链式存储时，插入第i个元素的时间与i的数值成正比。 因为存储空间是不连续的，插入第i个元素不需要移动其他元素。但是在插入之前从头搜索到第i个元素的指针，所以插入时间跟i相关

 

3.B、C你选对了

解析：  A、p->next->prev=s; p->next=s; s->prev=p; s->next=p->next; 先更改会造成原来的p结点后来的next信息丢失  B、p->next->prev=s; s->prev=p; s->next=p->next; p->next=s; 最后更改p->next是正确的，否则会造成原来的p结点后来的next信息丢失  C、s->next=p->next; p->next->prev=s; s->prev=p; p->next=s; 最后更改p->next是正确的，否则会造成原来的p结点后来的next信息丢失  D、s->prev=p; s->next=p->next; p->next=s; p->next->prev=s; 先更改p->next成s再更改p->next->prev，会造成原来的p结点后来的next信息丢失

 

4.(1)(n)

解析： 已知结点后插入，不需要移动其他结点位置，所以为O(1) 2. 先要查找到值为x的结点，需要O(n),再插入，不需要移动其他结点位置，需要O(1)，总共需要O(n)+O(1)=O(n)

5.tail->next=head

解析： 循环链表尾结点的next会指向头结点

 

part 2: 编程题

1.字符串插入

 

 

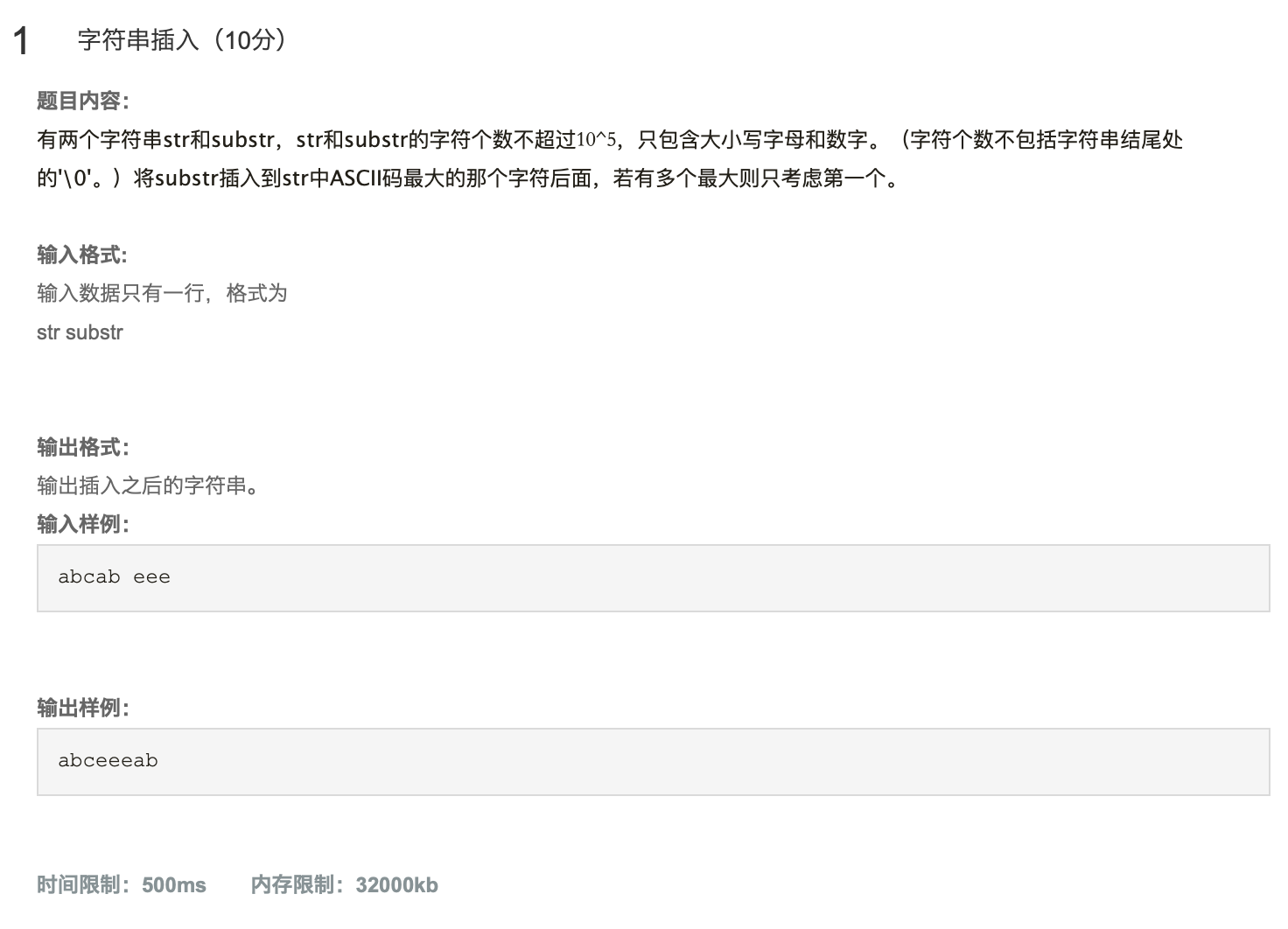
#include <iostream>
#include <cstring>
using namespace std;
int main(){
    char str[200010], substr[100010];
    int p=0, max_ascii=0, l1, l2;
    cin >> str >> substr;
    l1 = (int)strlen(str);
    l2 = (int)strlen(substr);
    for(int i=0; i<l1; ++i)
        if(str[i] > max_ascii){
            max_ascii = str[i];
            p = i;
        }
    for(int i=l1; i>p; --i)
        str[i+l2] = str[i];
    for(int i=p+1, j=0; j<l2; ++i, ++j)
        str[i] = substr[j];
    cout << str << endl;
    return 0;
}

 

2.大整数乘法

 

#include <iostream>
#include <cstring>
using namespace std;
int main(){
    int a[250]={0}, b[250]={0}, c[500]={0}, la,lb;
    string na, nb;
    //输入并倒序储存a和b
    cin >> na >> nb;
    la = (int)na.length();
    lb = (int)nb.length();
    for(int i=0; i<la; ++i)
        a[i] = na[la-i-1] - '0';
    for(int i=0; i<lb; ++i)
        b[i] = nb[lb-i-1] -'0';
    for(int i=0; i<la; ++i)//a的从低到高第i位
        for(int j=0; j<lb; ++j)//b的从低到高第j位
            c[i+j] += a[i] * b[j];
    for(int i=0; i<la+lb; ++i){//进位
        c[i+1] += c[i] / 10;
        c[i] %= 10;
    }
    int rest = c[la+lb]/10, lc = la+lb;
    while(rest){//进位
        c[lc] %= 10;
        c[++lc] = rest;
        rest = c[lc]/10;
    }
    for(; c[lc]==0 && lc; --lc);//找到最高的非零位
    for(int i=lc; i>=0; --i)
        cout << c[i];
    return 0;
}

3.约瑟夫问题

 

#include <iostream>
#include <cstring>
using namespace std;
int main(){
    bool monkey[300]={0};
    int n, m, cnt=0, cur=1, rest;
    cin >> n >> m;
    rest = n;
    for(int i=1; i<=n; ++i)
        monkey[i] = 1;
    while(rest > 1){
        ++cnt;//当前猴子报数
        if(cnt == m){//出圈,重新开始一轮报数
            --rest;
            monkey[cur] = 0;
            cnt = 0;
            //cout << cur << endl;
        }
        ++cur;//找到下一只报数的猴子
        while(monkey[cur] == 0){
            ++cur;
            if(cur > n)
                cur = 1;
        }
    }
    cout << cur << endl;
    return 0;
}