数据结构--树的性质

常见考点1结点数总度数1结点的度 ―― 结点有几个孩子(分支)树的度 ―― 各结点的度的最大值m叉树 ―― 每个结点最多只能有m个孩子的树常见考点2度为m的树、m叉树的区别常见考点3度为m的树第i层至多有mi−1个结点（i≥1m叉树第i层至多有mi−1个结点（i≥1常见考点4高度为h的m叉树至多有m−1mh−1个结点。

Joanh_Lan

968人浏览 · 2023-07-05 15:54:35

Joanh_Lan · 2023-07-05 15:54:35 发布

数据结构–树的性质

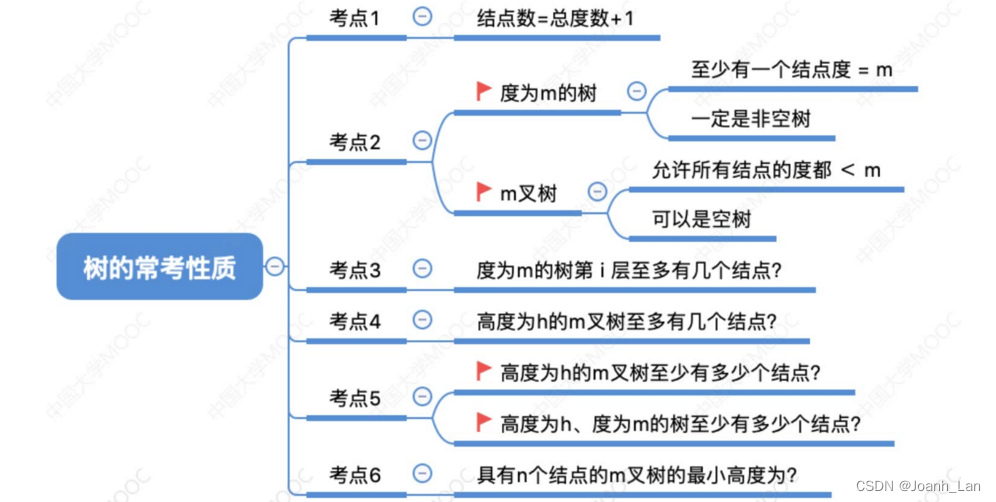
树的常考性质

$常见考点1:结点数=总度数+1\color{red}常见考点1:结点数=总度数+1$
结点的度 ―― 结点有几个孩子(分支)

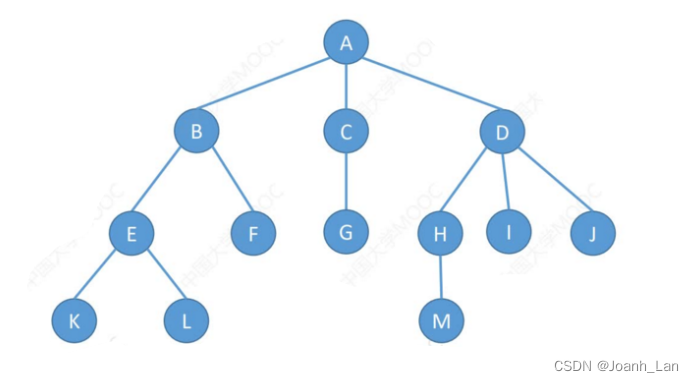
树的度 ―― 各结点的度的最大值
m叉树 ―― 每个结点最多只能有m个孩子的树

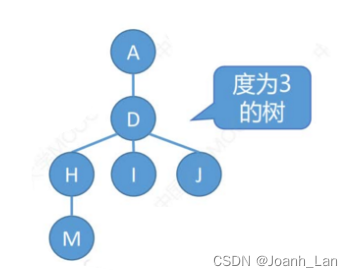
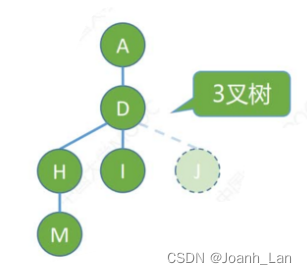
$常见考点2:度为m的树、m叉树的区别\color{red}常见考点2:度为m的树、m叉树的区别$

$常见考点3:度为m的树第i层至多有mi−1个结点（i≥1)\color{red}常见考点3:度为m的树第i层至多有m^{i-1}个结点（ i≥1)$
$m叉树第i层至多有mi−1个结点（i≥1)\color{red}m叉树第i层至多有m^{i-1}个结点（ i≥1)$

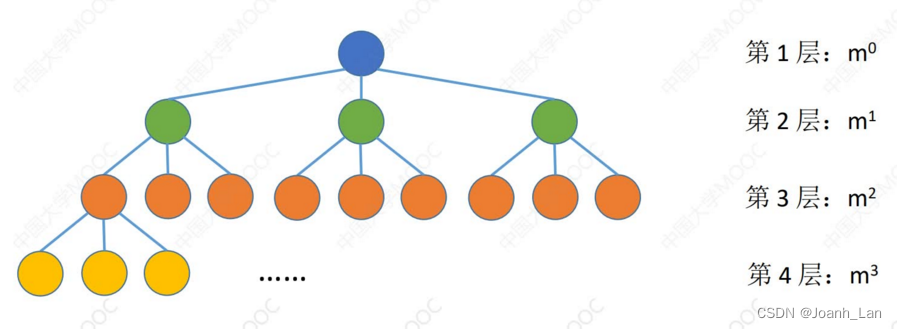
$常见考点4:高度为h的m叉树至多有mh−1m−1个结点。\color{red}常见考点4:高度为h的m叉树至多有\frac{m^{h}-1}{m-1}个结点。$

等比数列求和公式: $a+aq+aq2+⋅⋅⋅+aqn−1=a(1−qn)1−qa+aq+aq^{2}+\cdotp\cdotp\cdotp+aq^{n-1}=\frac{a(1-q^n)}{1-q}$

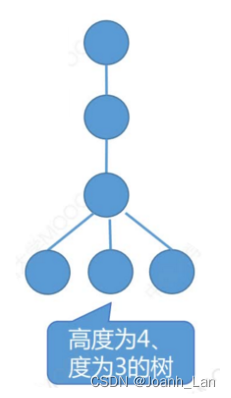
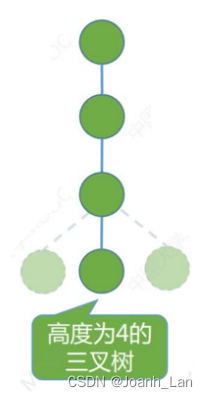
$常见考点5:高度为h的m叉树至少有h个结点。\color{red}常见考点5:高度为h的m叉树至少有h个结点。$
$高度为h、度为m的树至少有h+m−1个结点。\color{red}高度为h、度为m的树至少有h+m-1个结点。$

$常见考点6:具有n个结点的m叉树的最小高度为⌈log⁡m(ln⁡(m−1)+1)⌉\color{red}常见考点6:具有n个结点的m叉树的最小高度为\lceil\log_{\mathfrak{m}}(\ln(\mathfrak{m}-1)+1)\rceil$
高度最小的情况―—所有结点都有m个孩子

前h-1层最多有几个结点 $\frac{m^{{h-1}-1}{m-1}<n\leq\frac{m}h-1}{m-1} $前h层最多有几个结点

$mh−1<n(m−1)+1≤mhh−1<log⁡m(n(m−1)+1)≤hhmin=⌈log⁡m(n(m−1)+1)⌉\begin{aligned} &m^{h-1}<n(m-1)+1\leq mh \\ &h-1<\log_{\mathfrak{m}}(\text{n}(m-1)+1)\leq h \\ &h_{min}=\lceil\log_{\mathsf{m}}(n(m-1)+1)\rceil \end{aligned}$

知识点回顾与重要考点

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。