NumPy 背景与核心概念

矩阵与数组
矩阵是数学中按长方阵列排列的复数或实数集合，NumPy 中矩阵是二维数组的特殊形式，但通常直接使用更通用的 ndarray（N维数组）。ndarray 是 NumPy 的核心数据结构，支持高效的多维数据操作。

性能优势
NumPy 的底层由 C 语言实现，相比纯 Python 代码，其数组操作速度显著更快，尤其适合大规模数值计算。

数据类型
NumPy 仅有一种核心数据类型 ndarray，但支持多种元素类型（如 int32、float64 等），通过 dtype 属性指定。

---

1.创建 ndarray 的方法

通过 Python 序列
(1) 通过 Python 序列创建

# 一维数组
arr1 = np.array([1, 2, 3])       # 列表
arr2 = np.array((4, 5, 6))       # 元组

输出结果：
[1 2 3]
[4 5 6]

# 二维数组
arr3 = np.array([[1, 2], [3, 4]])           # 嵌套列表
arr4 = np.array([(1, 2), (3, 4)])           # 嵌套元组
arr5 = np.array([[1, 2], (3, 4)])           # 混合嵌套

输出结果：
[[1 2]
[3 4]]
[[1 2]
[3 4]]
[[1 2]
[3 4]]

# 多维数组
arr6 = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])  # 3D数组
print(arr6)

输出结果：
[[[1 2]
[3 4]]
[[5 6]
[7 8]]]

NumPy 内置函数
① np.arange()

# np.arange(stop): [0, stop)左闭右开区间
arr = np.arange(5)  # [0, 1, 2, 3, 4]

# np.arange(start, stop): [start, stop)左闭右开区间
arr = np.arange(2, 6)  # [2, 3, 4, 5]

# np.arange(start, stop, step)  step为步长
arr = np.arange(1, 10, 2)  # [1, 3, 5, 7, 9]

② np.ones() 全 1 数组

# 默认 float64
arr = np.ones((2, 3))  #创建2行3列的值全为1数组
# [[1., 1., 1.],
#  [1., 1., 1.]]

# 指定数据类型
arr = np.ones((2, 2), dtype='int32')  # [[1, 1], [1, 1]]

③ np.zeros() 全 0 数组

#创建3行2列的值全为0数组
arr = np.zeros((3, 2))  # [[0., 0.], [0., 0.], [0., 0.]]
arr_str = np.zeros(3, dtype=str)  # ['', '', '']转换成字符串格式

④ np.eye() 单位数组

arr = np.eye(3)  # 3x3 单位矩阵（对角线元素都为1）
# [[1., 0., 0.],
#  [0., 1., 0.],
#  [0., 0., 1.]]

⑤ 随机数组

# 0-1 随机小数
arr = np.random.random((2, 2))  
# [[0.123, 0.456],
#  [0.789, 0.321]]

# 随机整数 [low, high)
arr = np.random.randint(0, 10, size=(2, 3))  # size=(2, 3)指定形状为2行3列的数组
# [[3, 7, 2],
#  [8, 1, 9]]

# 均匀分布随机小数
arr = np.random.uniform(1.0, 5.0, size=3)  # [2.34, 4.56, 1.23] 生成3个1-5之间的随机小数

⑥ 等差数组 np.linspace()

# 生成 5 个从 0 到 10 的等差数列（包含端点）
arr = np.linspace(0, 10, 5)  # [ 0. ,  2.5,  5. ,  7.5, 10. ]

# 不包含端点
arr = np.linspace(0, 10, 5, endpoint=False)  # [0., 2., 4., 6., 8.]

# 返回步长
arr, step = np.linspace(0, 10, 5, retstep=True)  # step=2.5

2.数组属性与操作

常用属性

arr = np.array([[1, 2, 3], [4, 5, 6]])

print(arr.shape)   # (2, 3)  # 形状（行数，列数）
print(arr.ndim)    # 2       # 维度
print(arr.size)    # 6       # 元素总数
print(arr.dtype)   # int32   # 数据类型

类型转换

arr = np.array([1.5, 2.7, 3.2])#将浮点型改变为'int32'整数型数组
arr_int = arr.astype('int32')  # [1, 2, 3] 

形状操作

arr = np.arange(12).reshape(3, 4)#reshape形状为3行4列
# [[ 0,  1,  2,  3],
#  [ 4,  5,  6,  7],
#  [ 8,  9, 10, 11]]

# 打乱数组
np.random.shuffle(arr)  # 行顺序随机打乱

输出结果：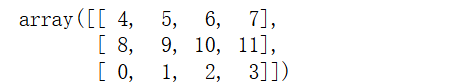

# 转置
arr_T = arr.T  # 行列互换

# 打平为一维数组
flat1 = arr.flatten()   # 返回副本
flat2 = arr.ravel()      # 返回视图（修改会影响原数组）
flat3 = arr.reshape(-1)  # 同 ravel()

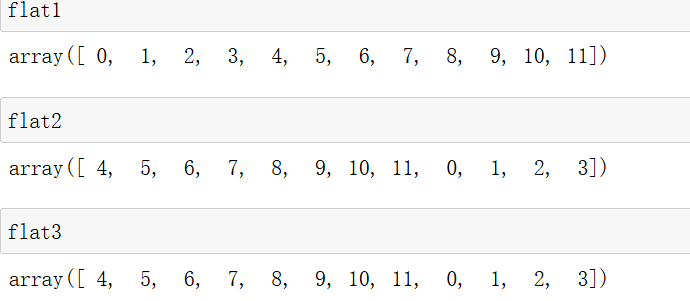
数组拼接与分割

• （1）拼接：

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])

# 垂直拼接（列数相同）
v_stack = np.vstack((a, b))  
# [[1, 2],
#  [3, 4],
#  [5, 6]]

# 水平拼接（行数相同）
h_stack = np.hstack((a, b.T))  
#b.T=[[5],
#     [6]]
# [[1, 2, 5],
#  [3, 4, 6]]

# 按维度拼接（升维）
stack = np.stack((a, b), axis=0)  # shape=(2, 3, 2)

• （2）分割：

arr = np.arange(16).reshape(4, 4)

# 按行均分
split1 = np.vsplit(arr, 2)  # 分成两个 2x4 数组

# 按列均分
split2 = np.hsplit(arr, 2)  # 分成两个 4x2 数组

# 不均等分割
split3 = np.array_split(arr, 3, axis=0)  # 分成 3 组（前多后少）

---

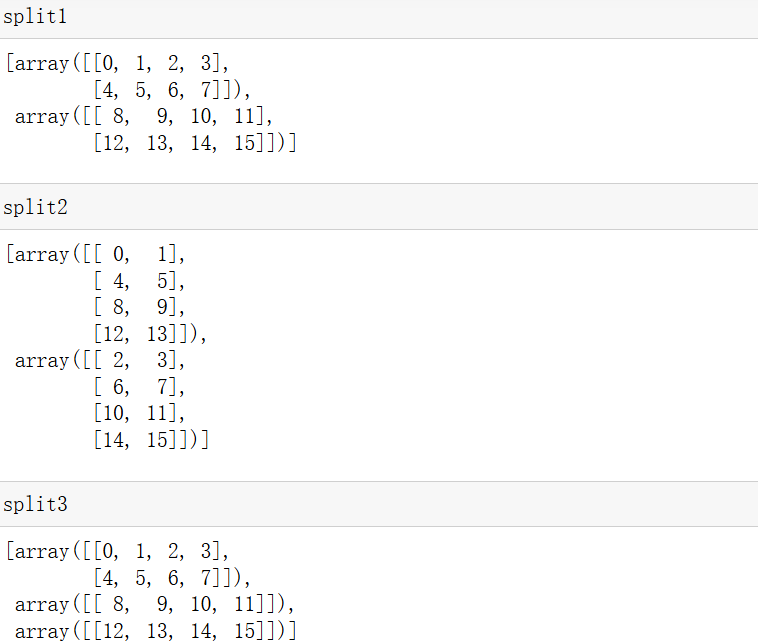
3.索引与切片

基础操作
位置索引:0，1，2，3，4…(从0开始)
（1）一维数组

arr = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

# 基本切片
print(arr[2:5])      # 输出: [2 3 4] (索引2到4)
print(arr[:4])       # 输出: [0 1 2 3] (从开始到索引3)
print(arr[5:])       # 输出: [5 6 7 8 9] (索引5到结束)
print(arr[::2])      # 输出: [0 2 4 6 8] (步长为2)
print(arr[::-1])     # 输出: [9 8 7 6 5 4 3 2 1 0] (反转数组)

（2）二维数组

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 索引
print(arr[0, 1])    # 2  # 第0行第1列

# 切片
print(arr[1, :])    # [4, 5, 6]  # 第1行所有列
print(arr[:, 2])    # [3, 6, 9]  # 所有行第2列
print(arr[0:2, 0:2])  # [[1, 2], [4, 5]]  # 左上角2x2区域

# 不连续索引
print(arr[[0, 2], [1, 2]])  # [2, 9]  # (0,1)和(2,2)位置的元素

# 布尔索引
mask = arr > 5
print(arr[mask])  # [6, 7, 8, 9]  # 所有大于5的元素

---

4.增删改查与统计

增删操作

arr = np.array([[1, 2], [3, 4]])

# 增（添加行）
new_row = np.array([[5, 6]])
arr = np.vstack((arr, new_row))  # [[1,2], [3,4], [5,6]]

# 删（删除第0行）
arr = np.delete(arr, 0, axis=0)  # [[3,4], [5,6]]

# 查（定位值）
print(arr[1, 1])  # 6

# 改（修改值）
arr[0, 0] = 10  # [[10,4], [5,6]]

统计函数
对于二维数组：
axis=0：表示沿着垂直方向（即按列）进行操作，即对每一列进行统计。
axis=1：表示沿着水平方向（即按行）进行操作，即对每一行进行统计。

arr = np.array([[1, 2, 3], [4, 5, 6]])

# 全局统计
print(np.sum(arr))      # 21
print(np.mean(arr))     # 3.5
print(np.std(arr))      # 1.7078  # 标准差
print(np.var(arr))      # 2.9167  # 方差

# 按行/列统计
print(np.sum(arr, axis=1))  # [ 6, 15]  # 每行求和
print(np.max(arr, axis=0))  # [4, 5, 6]  # 每列最大值

# 累计操作
print(np.cumsum(arr))  # [ 1,  3,  6, 10, 15, 21]
print(np.cumprod(arr)) # [ 1,  2,  6, 24, 120, 720]

---

5.特殊值与运算

NaN 与 Inf

1.nan (Not a Number)
nan 是一个特殊的浮点值，表示“不是一个数字”。它通常出现在以下情况：
（1）0 除以 0
（2）nan 参与的任何运算
（3）读取的外部数据中有缺失值
（4）负数的平方根（在实数范围内）
（5） 对负数取对数 使用 np.isnan() 函数可以检测数组中的 nan 值。

# 0 除以 0
result = 0 / 0.0  # 在 NumPy 中会得到 nan
print(result)  # nan

# 无穷大减去无穷大
inf = np.inf
result = inf - inf
print(result)  # nan

# 负数的平方根
result = np.sqrt(-1)
print(result)  # nan (并会给出警告)

# 任何涉及 nan 的运算
result = np.nan + 10
print(result)  # nan

arr = np.array([1, np.nan, 3, np.nan])
print(np.isnan(arr))
# 输出: [False  True False  True]

在数据分析中，我们通常需要填充或删除 nan 值。 常见方法：

• 用均值、中位数等填充
• 删除包含 nan 的行或列

arr = np.array([1, np.nan, 3, np.nan])
mean_val = np.nanmean(arr)  # 计算均值时忽略 nan
print(mean_val)  # 2.0
arr[np.isnan(arr)] = mean_val  # 将 nan 替换为均值
print(arr)  # [1. 2. 3. 2.]

2.inf (Infinity)
inf 表示无穷大，分为正无穷（np.inf）和负无穷（-np.inf）。它通常出现在以下情况：
（1）非零数除以 0
（2）超出浮点数表示范围的上限（溢出）
（3）对 0 取对数（负无穷）

# 正数除以0
result = 1.0 / 0.0
print(result)  # inf

# 负数除以0
result = -1.0 / 0.0
print(result)  # -inf

# 超出浮点数表示范围
result = 1e308 * 10  # 1e308 已经接近浮点数最大值，乘以10溢出
print(result)  # inf

# 对0取对数
result = np.log(0)
print(result)  # -inf
#使用 np.isinf() 函数可以检测数组中的无穷大值（包括正无穷和负无穷）。
arr = np.array([1, np.inf, -np.inf, 3])
print(np.isinf(arr))
# 输出: [False  True  True False]

注意事项：
nan 和 inf 都是浮点数类型，因此整数数组中不会出现它们（除非转换为浮点数）。
nan 与任何值（包括自身）比较都返回 False，因此检测 nan 必须使用 np.isnan()。

 print(np.nan == np.nan)  # False

算术与广播
(1)算术函数

arr = np.array([1.2, -2.7, 3.5])

# 向上/向下取整
print(np.ceil(arr))   # [ 2., -2.,  4.]
print(np.floor(arr))  # [ 1., -3.,  3.]

# 四舍五入
print(np.rint(arr))   # [ 1., -3.,  4.]

# 绝对值
print(np.abs(arr))    # [1.2, 2.7, 3.5]

# 条件选择
print(np.where(arr > 0, arr, 0))  # [1.2, 0., 3.5]  # 正数保留，负数变0

(2)广播机制
广播（Broadcasting）是 NumPy 的核心特性之一，它允许不同形状的数组进行算术运算，而无需显式复制数据。以下是广播机制的详细解释和示例：
广播核心规则

• 1.维度对齐：从最右边的维度开始向左比较
• 2.尺寸匹配： 满足以下任一条件即可广播
  维度尺寸相等
  其中一个维度尺寸为 1
  其中一个维度不存在（自动补 1）
• 3.扩展方式：尺寸为 1 的维度会自动复制扩展
  示例 1：一维数组与二维数组

a = np.array([[1, 2, 3], [4, 5, 6]])  # shape (2,3)
b = np.array([10, 20, 30])            # shape (3,) → 视为 (1,3)

# 广播过程：
# b 的形状 (1,3) → 扩展为 (2,3)
# [[10, 20, 30],
#  [10, 20, 30]]

print(a + b)
# 输出：
# [[11, 22, 33],
#  [14, 25, 36]]

示例 2：列向量与二维数组

c = np.array([[100], [200]])  # shape (2,1)

# 广播过程：
# c 的形状 (2,1) → 扩展为 (2,3)
# [[100, 100, 100],
#  [200, 200, 200]]

print(a * c)
# 输出：
# [[100, 200, 300],
#  [400, 500, 600]]

• 广播本质：自动扩展维度以匹配形状
• 核心规则：从右向左比较维度，尺寸为1或缺失的维度可扩展
• 应用场景：
  向量与矩阵运算
  标量与数组运算
  数据归一化
  条件筛选

---

6.字符串处理

数组操作

arr = np.array(['hello', 'world'])

# 拼接
print(np.char.add(arr, '!'))  # ['hello!', 'world!']

# 重复
print(np.char.multiply(arr, 2))  # ['hellohello', 'worldworld']

# 大小写转换
print(np.char.upper(arr))  # ['HELLO', 'WORLD']
print(np.char.capitalize(arr))  # ['Hello', 'World']

# 分割
print(np.char.split(arr[0], sep='l'))  # [['he', '', 'o']]

# 替换
print(np.char.replace(arr[0], 'l', 'x'))  # 'hexxo'

---

总结

以上内容涵盖 NumPy 的核心功能，适用于科学计算、数据分析等领域。NumPy 是数据分析的基石，掌握其核心操作（数组创建、索引、广播、统计函数）是高效处理数据的关键。通过上述示例，初学者可系统理解 NumPy 的功能并应用于实际场景。建议结合 Jupyter Notebook 逐步运行代码，观察输出结果加深理解。通过灵活组合这些操作，可高效处理多维数据。