[高级数据结构C++] 树状数组(求前缀和,区间和)
原理利用 负数 的补码。
》》》算法竞赛
/**
* @file
* @author jUicE_g2R(qq:3406291309)————彬(bin-必应)
* 一个某双流一大学通信与信息专业大二在读
*
* @brief 一直在算法竞赛学习的路上
*
* @copyright 2023.9
* @COPYRIGHT 原创技术笔记:转载需获得博主本人同意,且需标明转载源
*
* @language C++
* @Version 1.0还在学习中
*/
- UpData Log👆 2023.9.7 更新进行中
- Statement0🥇 一起进步
- Statement1💯 有些描述可能不够标准,但能达其意
技术提升站点
15 树状数组 BITree
15-1 适用
(高效的)查询和维护前缀和(或区间和)
前缀和:sum[x] = arr[1] + arr[2] + ... + arr[x]
区间和:SubArr = arr[ i ] +... + arr[ j ] = sum[ j ] - sum[ i - 1] (范围 [i , j] )
15-2 为何这么高效?
查询和维护都能达到O(log2n)的复杂度
看到这个复杂度不难想到 二分法 或 分治法 这种截半查找的算法,图论类似于 二叉树 这种数据结构。
15-3 实现方法
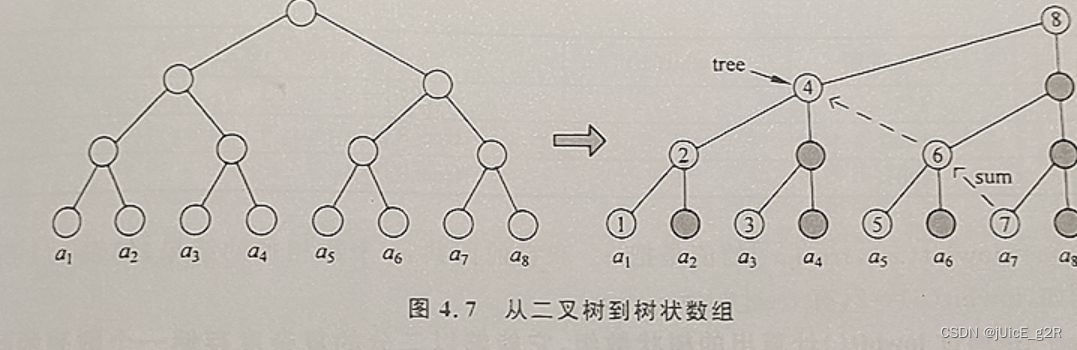
注: 图右的虚线是前缀和 sum[ 7 ] 的计算过程。
BITree[1] = a1;
BITree[2] = BITree[1] + a2;
BITree[3] = a3;
BITree[4] = BITree[2] + BITree[3] + a4;
...
BITree[8] = BITree[4] + BITree[6] + BITree[7] + a8;
容易看出:前缀和 sum[ 8 ] = BITree[ 8 ] ,体现了树状数组可以快速查询前缀和的特性。
还有个特性就是 **维护快 **。如果要修改 a3 的话,根据上图可知 a3 这个元素会影响 BITree[ 3 ] 和 左树主干上的数据:BITree[ 4 ] 与 BITree[ 8 ](而 BITree[ 6 ] 在右树上,不受影响),实际上修改的就是自己以及父节点( 子节点 x 的父节点可以根据 lowbit(x) 函数进行得出)。
15-4 lowbit 函数查找 父节点 规律是如何寻找到的?
如:
sum[7] = BITree[7] + BITree[6] + BITree[4]
- 查询步骤
7 的二进制是 111,去掉最后的1,变成 110(即 6),则有成员 BITree[6]
再去掉一个,变成 100(即 4),则有成员 BITree[4]。
- 维护步骤
3 的二进制为 11,在最后的 1 上加 1 ,变成 100(即 4),则有成员 BITree[4] 需要修改
在 100 的最后一个 1 上加 1 ,变成 1000(即8),则有成员 BITree[8] 需要修改
- 无论是查询还是维护一个元素,都需要查找当前元素所对应二进制的最后一个1
15-5 这里涉及一个 反码 与 补码 的芝士
(注:最高位为符号位,0表正,1表负)
正数的反码就是本身,负数的反码是除开符号位外,其他各位均取反
1011 ---反码---> 1100
正数的补码就是本身,负数的补码是对应反码+1
1011 ---补码---> 1100 + 0001 = 1101
15-6 lowbit(x)
lowbit(x) = x & (-x) ,查找当前元素所对应二进制的最后一个1。原理利用 负数 的补码。
#define lowbits(x) ((x) & (-x))
注:1 & 0 = 0 ;1 & 1 = 1 ;0 & 0 = 0
| x | x的二进制 | lowbit(x)【BIN】 | res【DEC】 | tree[x] |
|---|---|---|---|---|
| 1 | 1 | 1 & (0+1) = 12 | 1 | BITree[1] = a1 |
| 2 | 10 | 10 & (01+01) = 102 | 2 | BITree[2] = a1+ a2 |
| 3 | 11 | 11 & (00+01) = 012 | 1 | BITree[3] = a3 |
| 4 | 100 | 100 & (011+001) = 1002 | 4 | BITree[4] = BITree[2] + BITree[3] + a4 |
| 5 | 101 | 101 & (010+001) = 0012 | 1 | BITree[5] = a5 |
| 6 | 110 | 110 & (001+001) = 0102 | 2 | BITree[6] = a5 + a6 |
| 7 | 111 | 111 & (000+001) = 0012 | 1 | BITree[7] = a7 |
| 8 | 1000 | 1000 & (0111+0001) = 10002 | 8 | BITree[8] = BITree[7] + a8 |
- BITree[x] 中存储的区间为
[x-res+1 , x]
注:实际上在存储数据时不会用到二维数组来存储,上述只是图论形式!!!
15-7 单点维护 + 查询区间和
#include<bits/stdc++.h>
using namespace std;
#define lowbits(x) ((x) & (-x))
const int MAX=8;
vector<int> a(MAX,0);
vector<int> BITree(MAX,0); //前缀和
void Update(int id,int new_data){ //维护数据
int temp=id;
int increse=new_data-a[id]; //获取修改结点的增量
while(temp<=MAX){
BITree[temp]+=increse; //对每个父节点都要修改增量
temp+=lowbits(temp); //向前反推父节点直到根节点停止
}
}
int GetSum(int id){ //前缀和
int sum=0; int temp_id=id;
while(temp_id>0){
sum+=BITree[temp_id];
temp_id-=lowbits(temp_id);
}
return sum;
}
int main(void){
for(int i=1;i<=MAX;i++)
Update(i,i);
printf("区间[2,6]的和:%d",GetSum(6)-GetSum(2-1)); //求SubArr=GetSum[j]-GetSum[i-1]
}
15-8 区间维护
区间维护(修改)是指对一个区间的每个元素都增加(或减少)同一个值
实现这个功能只需要在原来单点维护 的功能基础上添加差分数组即可
15-8-1 为何使用差分数组
1、差分数组有 D[k] = a[k] - a[k-1],则有 a[k] = D[1] + D[2] + ... + D[k] ,可以看出 差分 是 前缀和 的逆运算,把求 a[k] 变成了求 D[k] 的前缀和,树状数组很适合处理 前缀和 问题。
2、同时对多个连续元素进行相同的加减操作,这些被操作的元素的 差分数组值 D[k] 是不会改变的。
15-8-2 如何对区间【L,R】操作
实际上处理的是差分数组:
//伪代码
D[L] += increse; //共同变化增量值increse
D[R+1] -= increse;
- 差分数组很巧妙的将对多个数据操作的问题变为处理端点的问题
//实际代码
int Update(int id,int d){...}//对原函数稍加修改
Update( L, increse);
Update(R+1,-increse);
15-9 二阶树状数组
线段树 1(HDU 3372)
要求
一个数列,进行两个操作:
1、把某个区间每个数加 d
2、求某区间的所有数之和
INPUT
第一行输入两个整数 n(该数列数的个数),m(要操作的数的个数)
第二行输入 n 个数
后面 m行:表示操作
1)输入
1 L R d表示将区间每个数加d2)输入
2 L R d表示算出区间和OUTPUT
输出多行2)的结果
-
思路展示
-
求
区间和即求两端点前缀和之差 -
a1+a2+ … +ak
= D1 + (D1 + D2) + … +( D1 + D2 + … + Dk)
= kD1 + (k - 1)D2 + (k - 2)D3 + … + (k - (k - 1))Dk
= k(D1+ … + Dk) + (D2 + 2D3 + … + (k-1)Dk)=k ∑ Di + ∑(i-1)Di
最后一行求两个前缀和,用两个树状数组分别处理,一个是 Di,一个是 (i-1)Di
- 代码展示
#include<bits/stdc++.h>
using namespace std;
using LL=long long int;
#define lowbits(x) ((x) & (-x))
const int MAX=8;
vector<int> a(MAX,0);
void Update(int id,int d,vector<int>& BITree){ //维护数据
int temp=id;
while(temp<=MAX){
BITree[temp]+=d; //对每个父节点都要修改增量
temp+=lowbits(temp); //向前反推父节点直到根节点停止
}
}
int GetSum(int id,vector<int>& BITree){ //前缀和
int sum=0; int temp_id=id;
while(temp_id>0){
sum+=BITree[temp_id];
temp_id-=lowbits(temp_id);
}
return sum;
}
int main(void){
vector<int> BITree1(MAX,0); // Di 前缀和
vector<int> BITree2(MAX,0); //(i-1)Di 前缀和
vector<int> D(MAX,0); //差分数组
int n,m; scanf("%d %d",&n,&m);
int last,cur=0;
for(int i=1;i<=n;i++){
scanf(" %d",&cur);
D[i]=cur-last;
Update(i, D[i],BITree1);
Update(i,(i-1)*D[i],BITree2);
last=cur;
}
while(m--){
int op,L,R,increse;
scanf("%d",&op); //输入操作编号
if(op==1){ //执行操作1:区间内同时加一个增量
scanf(" %d %d %d",&L,&R,&increse);
Update( L, increse,BITree1);
Update(R+1, -increse,BITree1);
Update( L,(L-1)*increse,BITree2);
Update(R+1, R*(-increse),BITree2);
}
else{ //执行操作2:算出对应区间和
scanf(" %d %d",&L,&R);
int sumL_1=(L-1)*GetSum(L-1,BITree1) - GetSum(L-1,BITree2);
int sumR = R*GetSum( R,BITree1) - GetSum( R,BITree2);
printf("%d\n",sumR-sumL_1);
}
}
return 0;
}
补充知识:vector容器当参数传递
- vector传参的三种方式:
void func1(vector<int> vet); //调用拷贝构造函数,形参改变不会影响到实参
void func2(vector<int> &vet); //不调用拷贝构函数,形参改变影响到实参
void func3(vector<int> *vet); //不调用拷贝构函数,形参改变影响到实参
- 具体代码
void func1(vector<int> vet){ //传送数值
vet.emplace_back(1);
}
void func2(vector<int> &vet){ //引用
vet.emplace_back(2);
}
void func3(vector<int> *vet){ //指针
vet->emplace_back(3); //指针用 ->
}
int main() {
vector<int> vet;
func1(vet);
cout << vet[0] << endl; //!!!报错,因为实参不会改变(想正常运行可注释掉这句)
vector<int> vet2;
func2(vet2);
cout << vet2[0] << endl; //输出 2
vector<int> vet3;
func3(&vet3); //这里取得是指针
cout << vet3[0] << endl; //输出 3
return 0;
}
点击继续进阶学习

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容







所有评论(0)