深入理解数据结构原理(2)—树(Tree)

目录一、树的定义1、树的性质1.1、树有以下特点1.2、树的属性描述1.3、树的基本性质二、二叉树1、二叉树的定义2、二叉树的性质3、二叉树的遍历4、二叉树的储存结构5、平衡二叉树6、哈夫曼树一、树的定义树在书中的定义：是有 n（n>0）个结点的有限集。当 n = 0 时称为空树。其中树有且只有一个特定的根结点，任何一颗非空树只有一个根结点。（其实就是像树一样长出的一个一个分支，每个开叉处的

皮皮治

1649人浏览 · 2022-05-11 00:32:15

皮皮治 · 2022-05-11 00:32:15 发布

一、树的定义

树在书中的定义：是有 n（n>0）个结点的有限集。当 n = 0 时称为空树。

其中树有且只有一个特定的根结点，任何一颗非空树只有一个根结点。（其实就是像树一样长出的一个一个分支，每个开叉处的结就是一个一个的结点，树杆就是这里的边，树上还有叶子等）

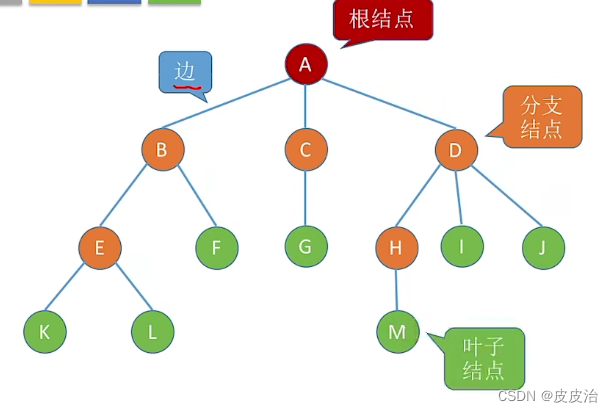
边：每个结点到下一个结点的分支。

分支结点：有下一级的结点，或者叫做有前驱和后驱的结点。

叶子结点：没有下一级的结点，或者叫做没有后驱的结点。（前驱就是向上一级，后继是向下一级）

每个大树下又可以分为很多个子树；

森林：森林是m (m≥0）棵互不相交的树的集合

树还可以分为有序树和无序树：

有序树――逻辑上看，树中结点的各子树从左至右是有次序的，不能互换

无序树――逻辑上看，树中结点的各子树从左至右是无次序的，可以互换

从上面可以看出树是一种递归的思想，是一种递归的数据结构

每个结点都可以有0个或者多个后继。
除了根结点外，任意一个结点都有且仅有一个前驱。

1、树的性质

1.1、树有以下特点

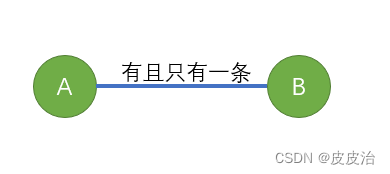
（1）在一棵树中两个结点之间只有唯有且仅有唯一的一条路径连通。

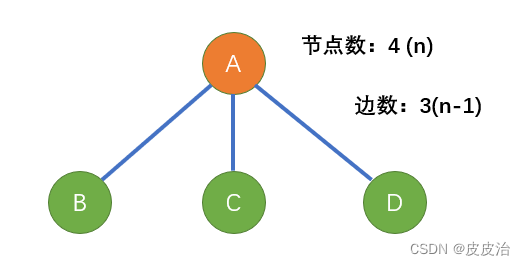
（2）在一棵树如果有 n 个结点，那么它一定恰好有 n-1 条边。例如：

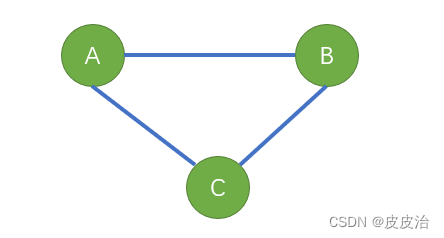
（3）一棵树不包含回路，错误示范如下：

1.2、树的属性描述

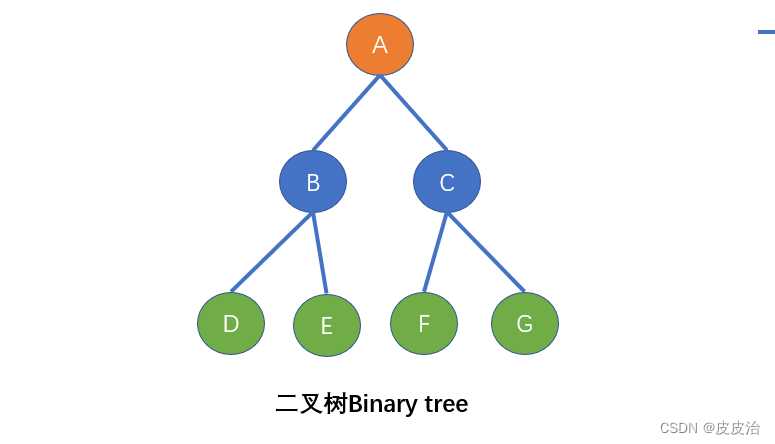
如下图是一棵树，且是一棵二叉树

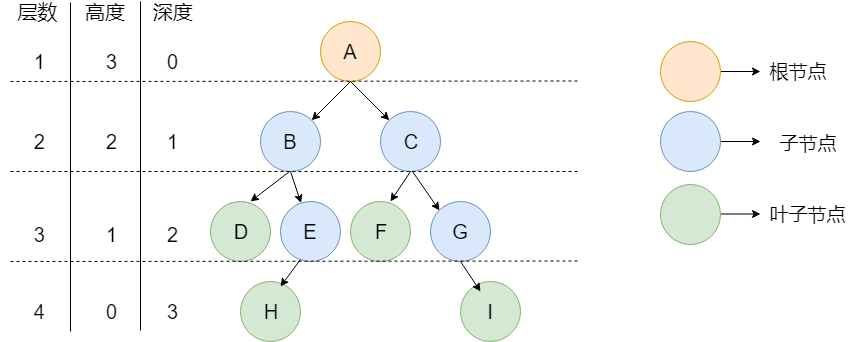
节点：树中的每个元素都可以统称为节点。
根节点 ：顶层节点或者说没有父节点的节点。上图中 A 节点就是根节点。
父节点 ：若一个节点含有子节点，则这个节点称为其子节点的父节点。上图中的 B 节点是 D 节点、E 节点的父节点。
兄弟节点 ：具有相同父节点的节点互称为兄弟节点。上图中 D 节点、E 节点的共同父节点是 B 节点，故 D 和 E 为兄弟节点。
结点的高度：从下边往上数；
结点的层次（深度）：从上面往下数；
树的高度：就是指树的层数；
结点的度：是指结点下一级有几个分支；（看结点的分支）
树的度：是指全部结点的度的最大值；（看全部结点哪个分支最大就是树的度）

1.3、树的基本性质

（1）结点数 = 总度数 + 1。

（2）度为m的树(或者m叉树)中第i层上至多有 $m^{i-1}$ 个结点（ $i\geq 1$ ）。

如： $3^{0}=1$ 、 $3^{1}=3$ 、 $3^{2}=9$ ……

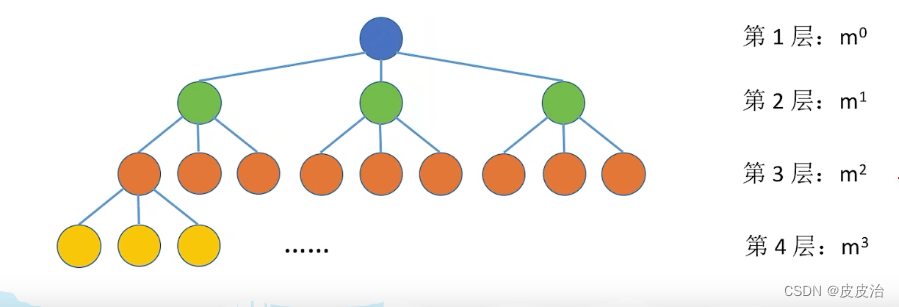
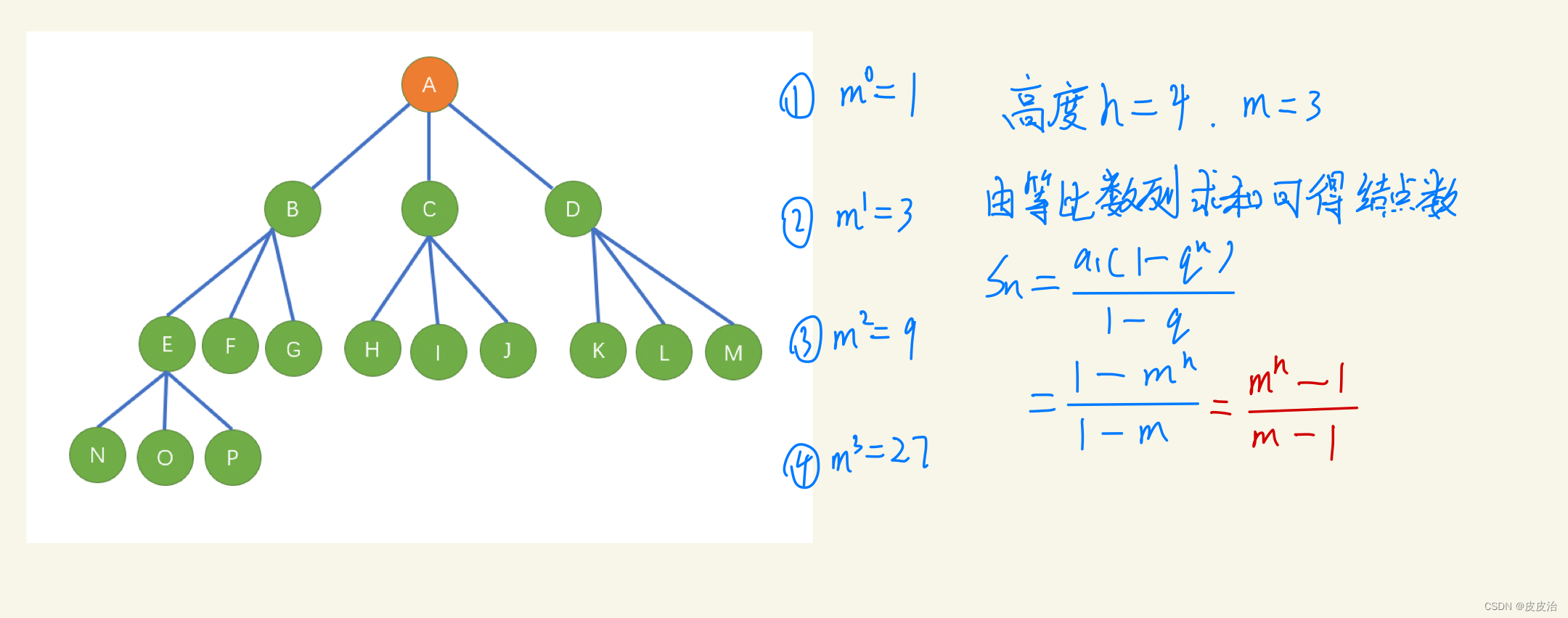
（3）高度为h的m叉树至多有 $\frac{m^{h}-1}{m-1}$ 个结点。

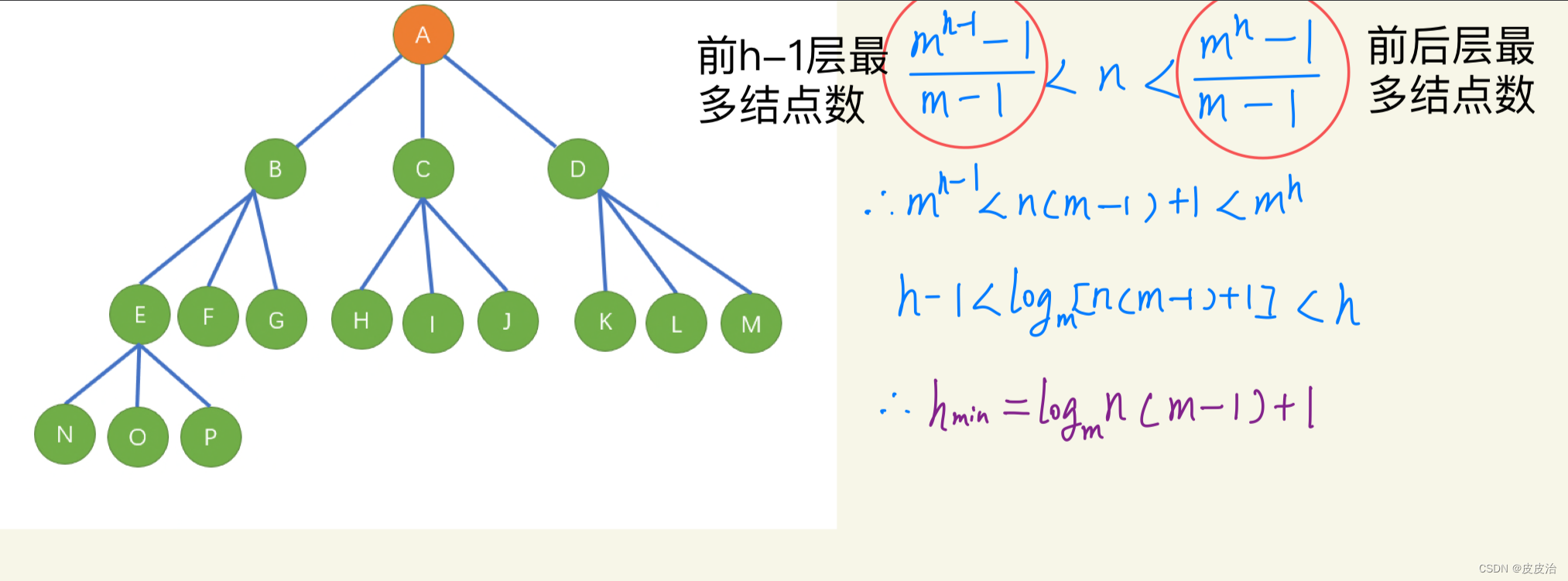
（4）具有n个结点的m叉树的最小高度为 $\left [ \log _{m}\left ( n\left ( m-1 \right )+1 \right ) \right ]$

二、二叉树（Binary tree）

1、二叉树的定义

二叉树（Binary tree）：就是每个结点的分支嘴都含两个分支的（不存在分支大于2的结点）树结构，且每个结点的分支次序不能任意颠倒（也就是说二叉树是有序的树）。

或者说由一个根结点，和两个互不相交的根组成的树，其中两个根叫做左子树和右子树。

从定义中我们可以看出一个二叉树中的每个结点只能含有0、1、或2个分支。

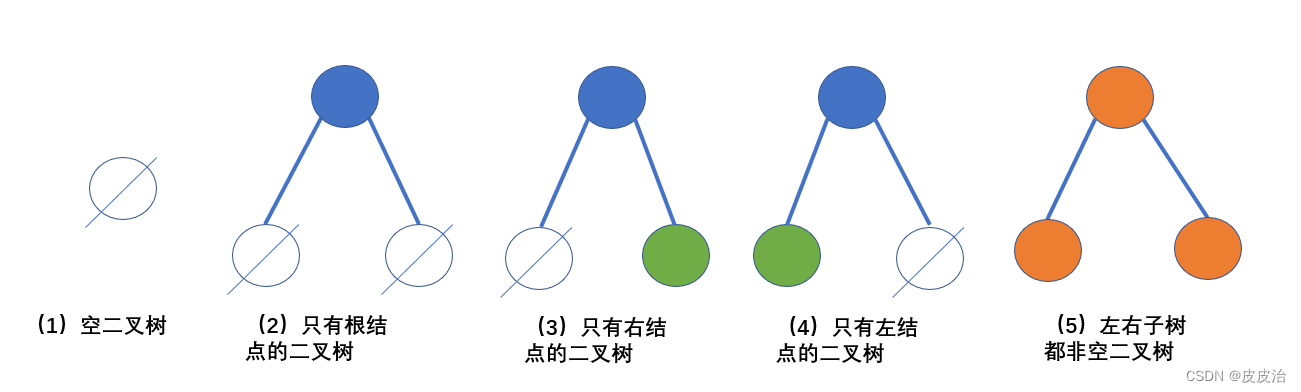
二叉树的五种基本形态如下：

2、二叉树的分类和性质

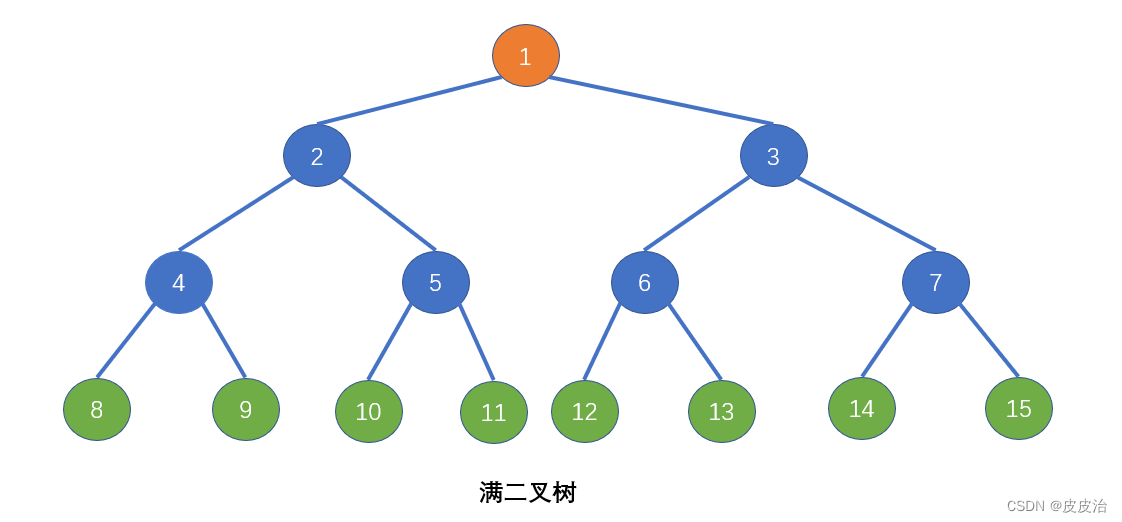
2.1、满二叉树

满二叉树（除了叶子结点外，其余结点都长满两个分支的树）。

（1）一棵高度为h，且含有 $2^{h}-1$ 个结点的二叉树。

由上面1.3、树的基本性质可知， 高度为h的m叉树至多有 $\frac{m^{h}-1}{m-1}$ 个结点，所以把m=2，带进可得二叉树最多结点数 $2^{h}-1$ 个。

满二叉树的特性

只有最后一层有叶子结点。
不存在度为1的结点。
按层序从1开始编号，结点 i 的左孩子为 2i，右孩 2i+1 ，结点 i 的父节点为 [i/2]。(比如5的左孩子为10，有孩子为11，刚好符合公式)

2.2、完全二叉树

完全二叉树：就是除了最后一层外，若其余层都是满的（也就是说最后一层是满的或者不是满的，并且不满的是在右子树缺少连续若干节点）。

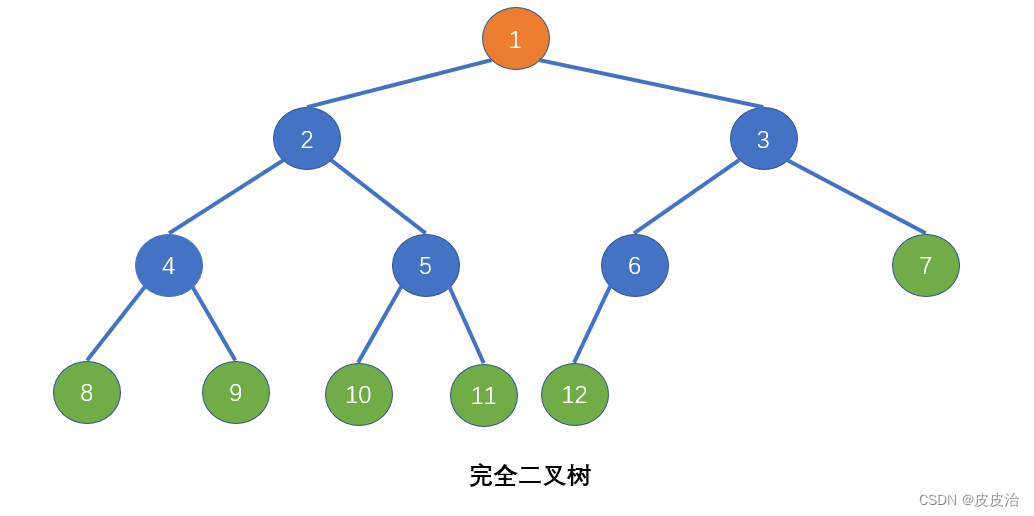
完全二叉树的特性

只有最后两层有出现叶子结点。
最多存在一个度为1的结点。
按层序从1开始编号，结点 i 的左孩子为 2i，右孩 2i+1 ，结点 i 的父节点为 [i/2]。(比如5的左孩子为10，有孩子为11，刚好符合公式)。
当结点数 $i\leqslant \left [ n/2\right ]$ 为分支结点，且 i>[n/2] 为叶子结点。

2.3、平衡二叉树

平衡二叉树：是一棵（排序树）、可以是一棵空树，如果它不是空树，那么它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。

关于平衡二叉树可以看这位博主的：

平衡二叉树_月雲之霄的博客-CSDN博客_平衡二叉树

2.4、什么是二叉排序树？

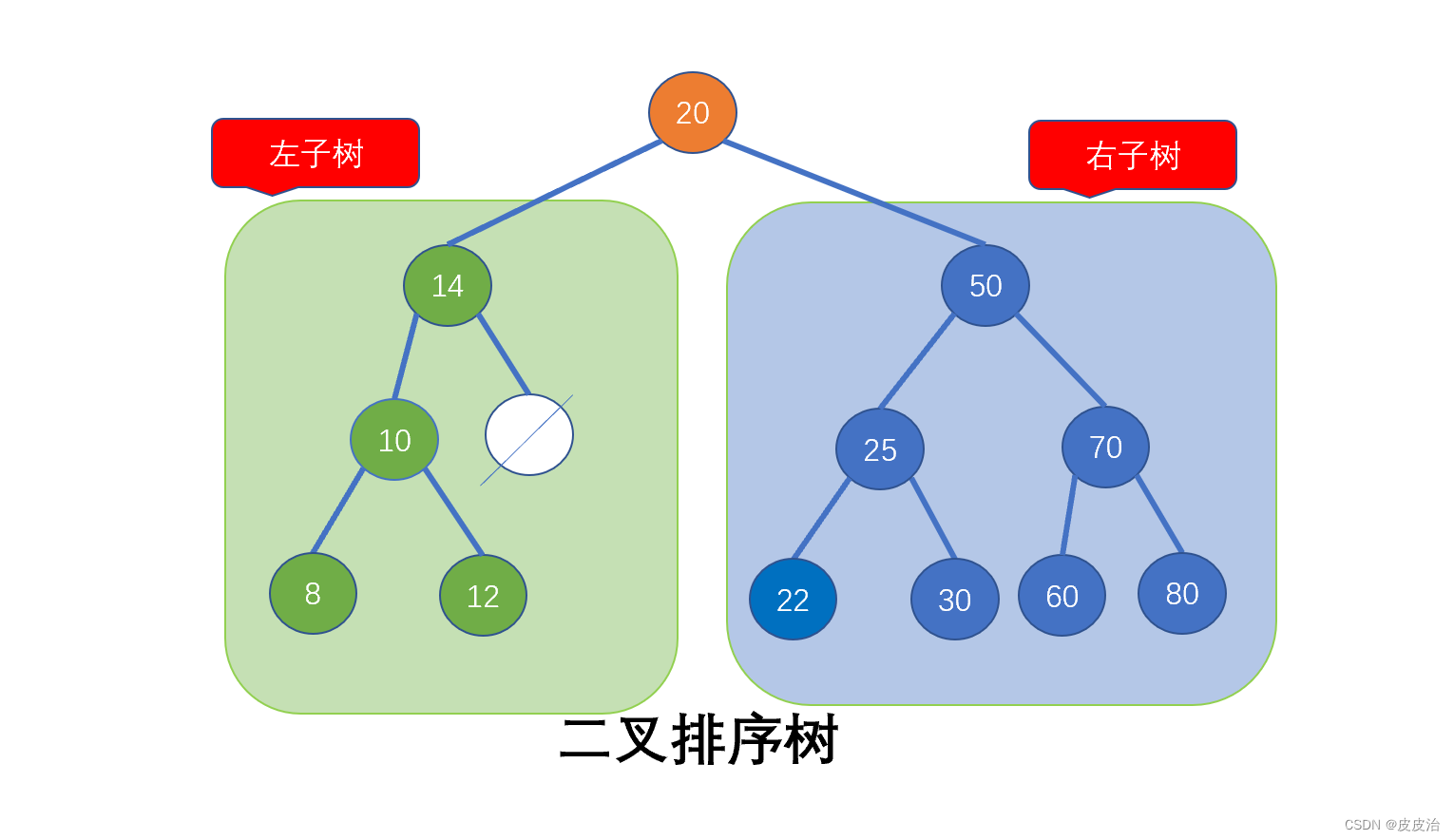
二叉排序树（Binary Sort Tree）：是一棵二叉树或者是空二叉树；或者是具有如下性质的二叉树

左子树上所有结点的关键字均小于根结点的关键字。

右子树上所有结点的关键字均大于根结点的关键字。

左子树和右子树又各是一棵二叉排序树。

3、二叉树的储存结构

3.1、顺序储存结构

3.2、链式储存结构

4、二叉树的遍历

二叉树的遍历记忆顺序

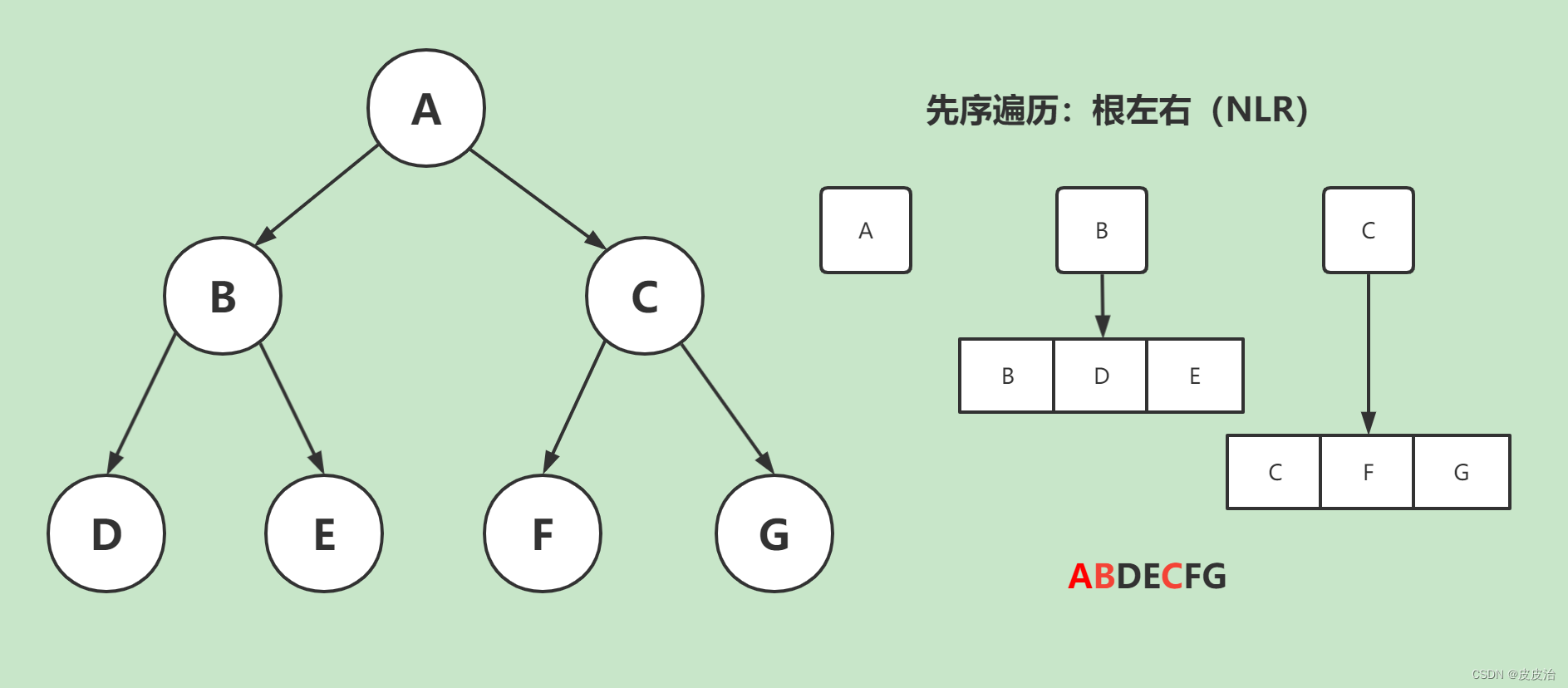
先序遍历：根左右（NLR）
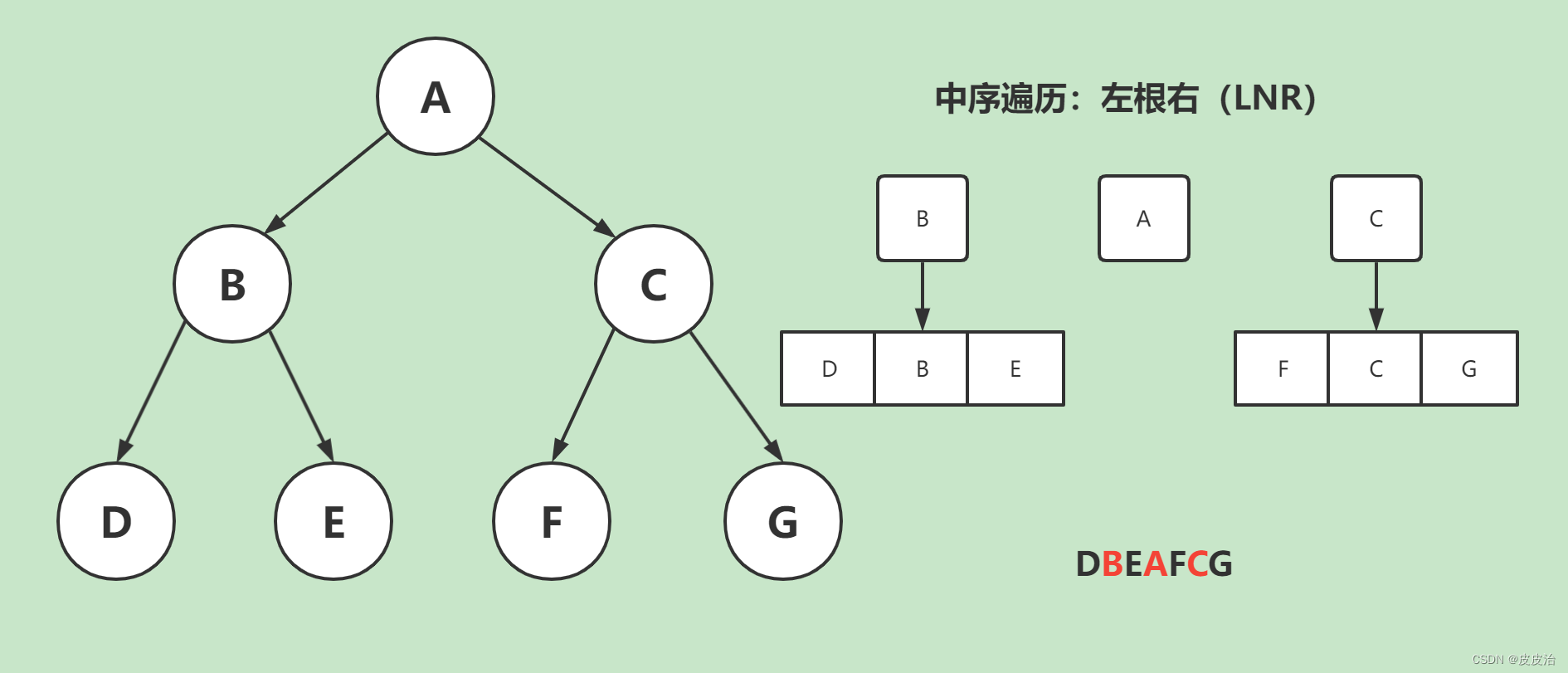
中序遍历：左根右（LNR）
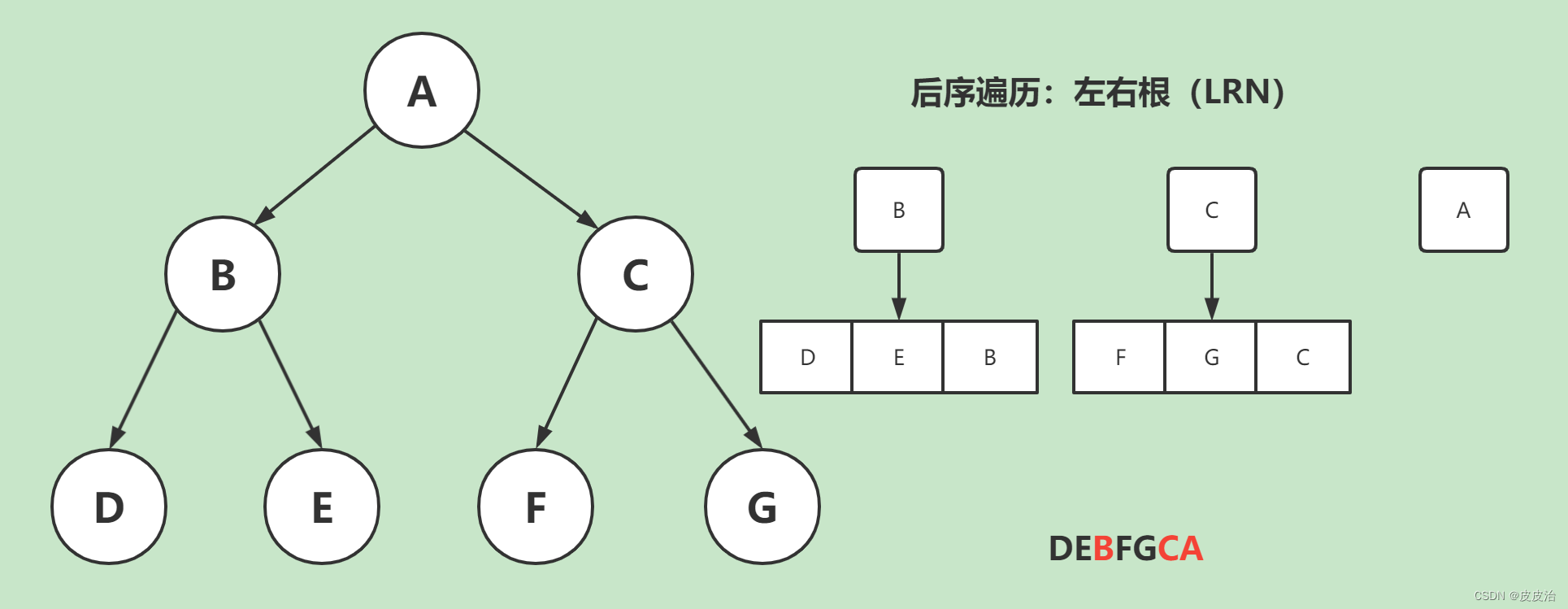
后序遍历：左右根（LRN）

4.1、先序遍历

4.2、中序遍历

4.3、后序遍历

5、哈夫曼树

6、红黑树

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。