数据结构学习记录——平衡二叉树的调整(基本介绍、右单旋、左单旋、左右双旋、右左双旋、平衡因子的计算)
数据结构学习记录——平衡二叉树的调整(基本介绍、右单旋、左单旋、左右双旋、右左双旋、平衡因子的计算)平衡二叉树也是一棵二叉搜索树。当我们在一棵平衡二叉树进行插入或者删除时,可能会把原来的平衡二叉树变得不平衡,这个时候我们就需要进行调整了。RR旋转(右单旋)LL旋转(左单旋)RL旋转(右左双旋)LR旋转(左右双旋)
目录
基本介绍
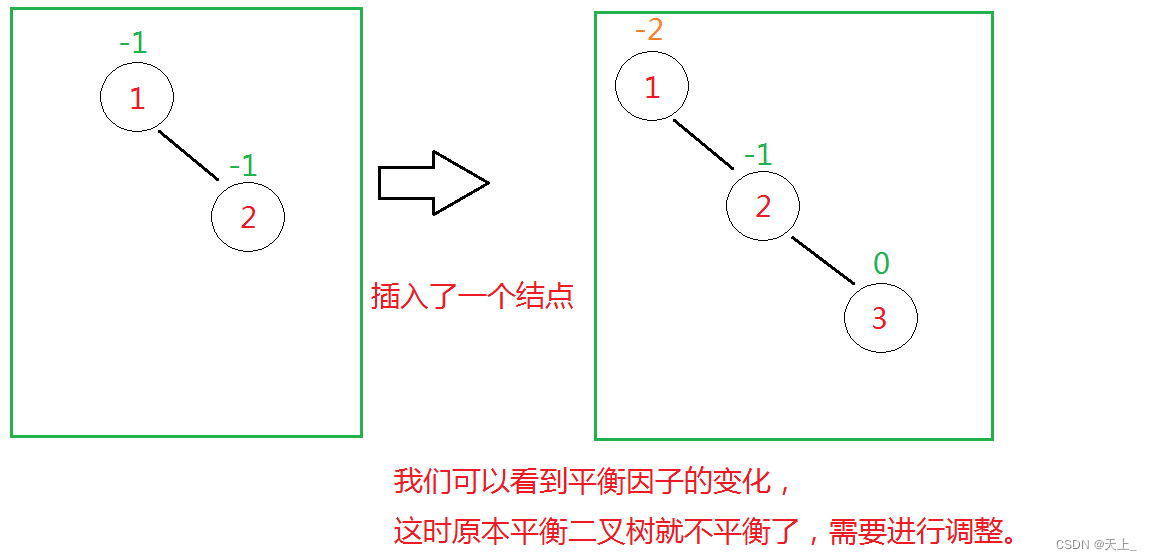
首先,平衡二叉树也是一棵二叉搜索树。
当我们在一棵平衡二叉树进行插入或者删除时,可能会把原来的平衡二叉树变得不平衡,
这个时候我们就需要进行调整了。
平衡二叉树的调整主要分为四大类:
- RR旋转(右单旋)
- LL旋转(左单旋)
- RL旋转(右左双旋)
- LR旋转(左右双旋)
右单旋
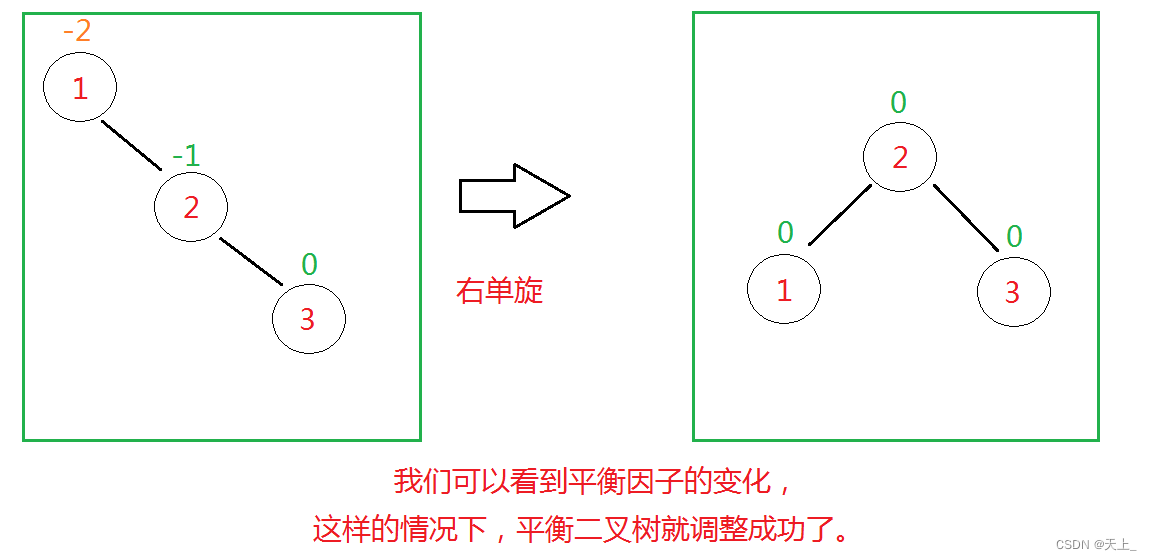
我们抽象化出两个概念:“发现者”、“麻烦结点”。 (或者说“被破坏者”和“破坏者”)
不平衡的“发现者”是1,“麻烦结点”为破坏了平衡的节点。
“麻烦结点”3在“发现者”右子树的右子树上,因而叫RR插入,需要RR旋转(右单旋)。
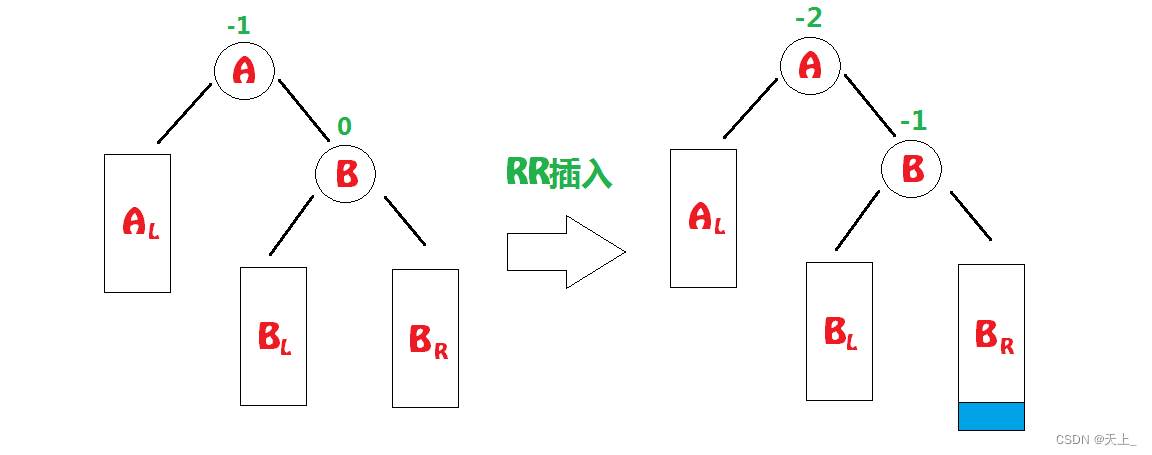
要注意的是:
插入到蓝色区域时,插入到其左子树或者右子树,处理方式都是一致的。
当发生了RR插入时,我们要进行RR旋转(右单旋):
把B拎上来,且因为平衡二叉树也是二叉搜索树,要比B小,比A大,所以
要放在B的左子树、A的右子树上。
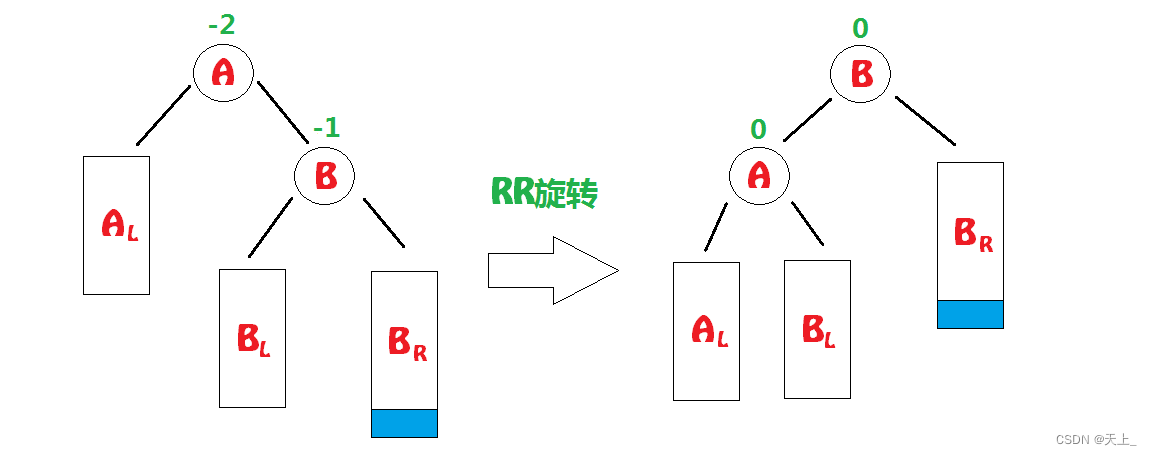
左单旋
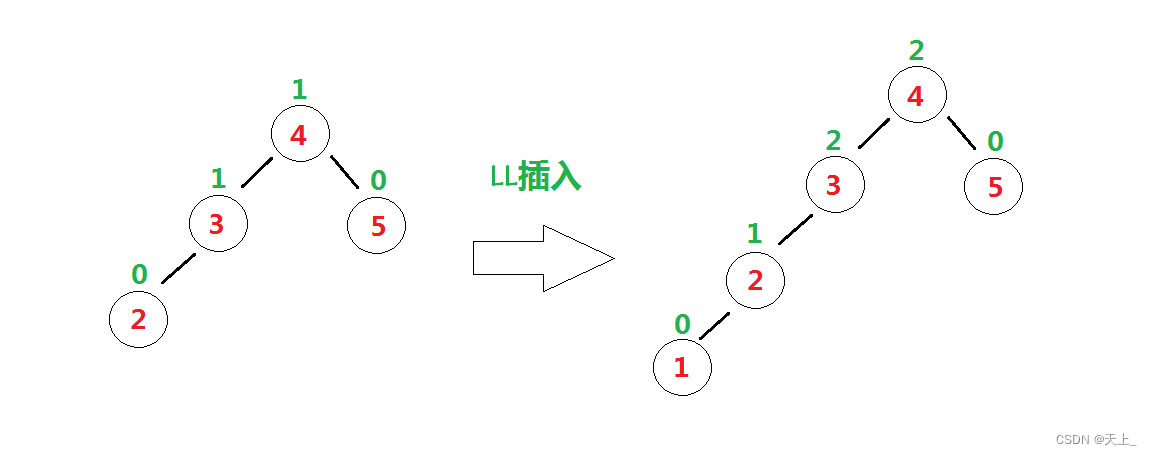
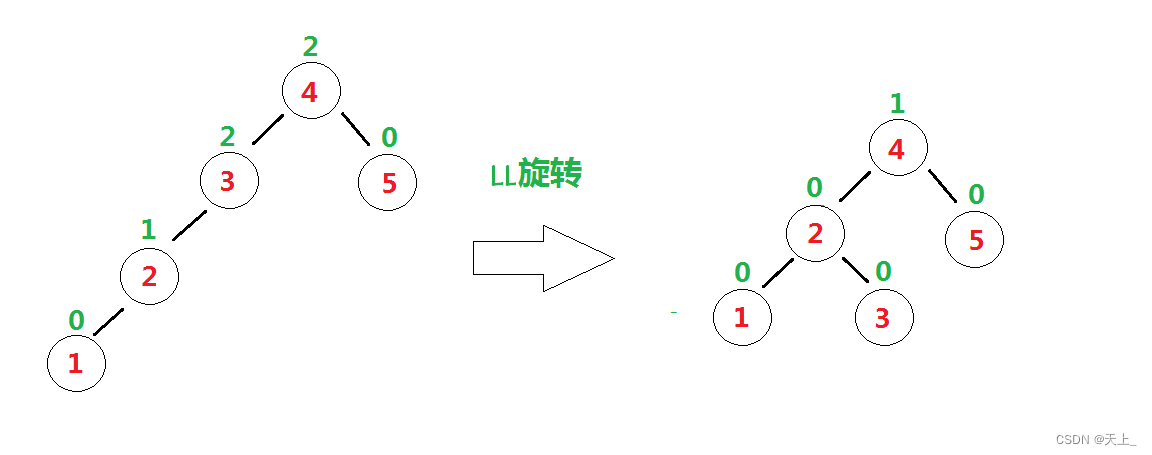
“发现者”是结点3,“麻烦结点”1在“发现者”左子树的左子树上。
故而需要进行LL旋转(左单旋)
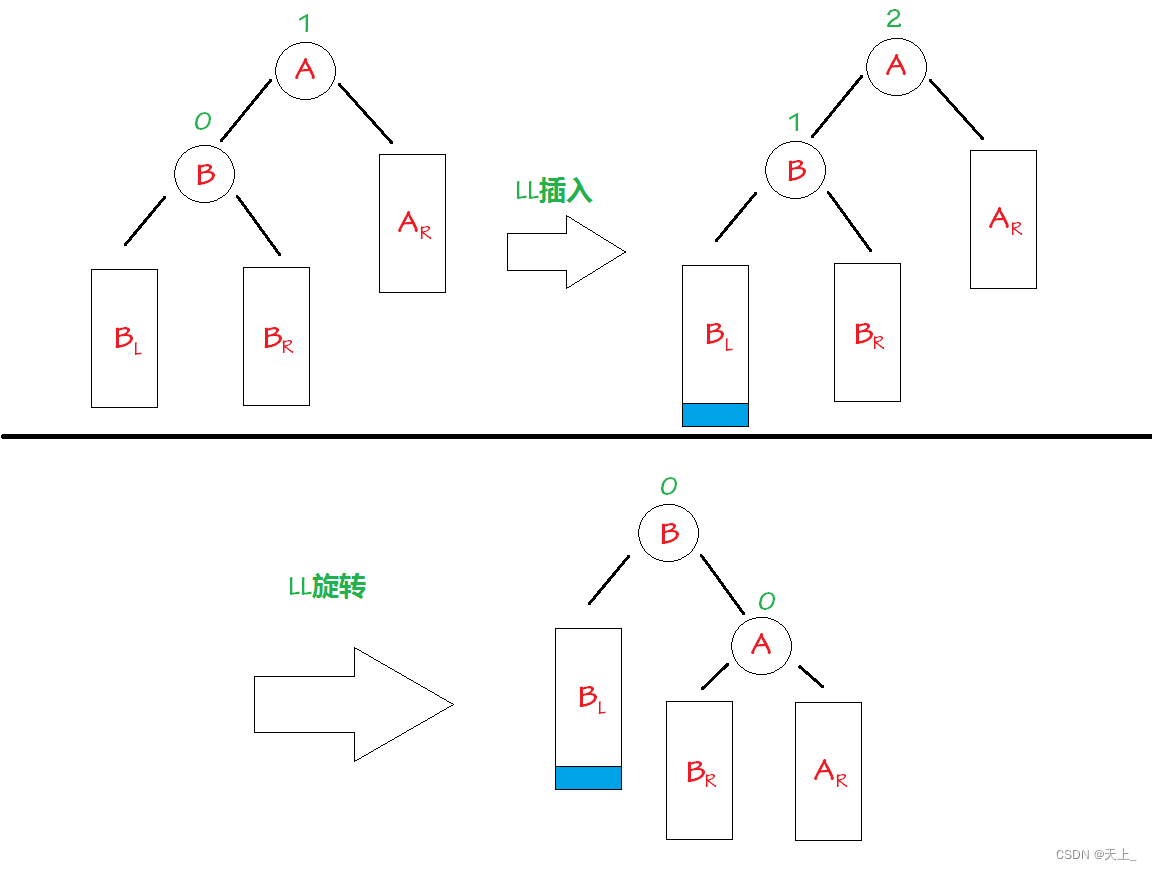
左右双旋
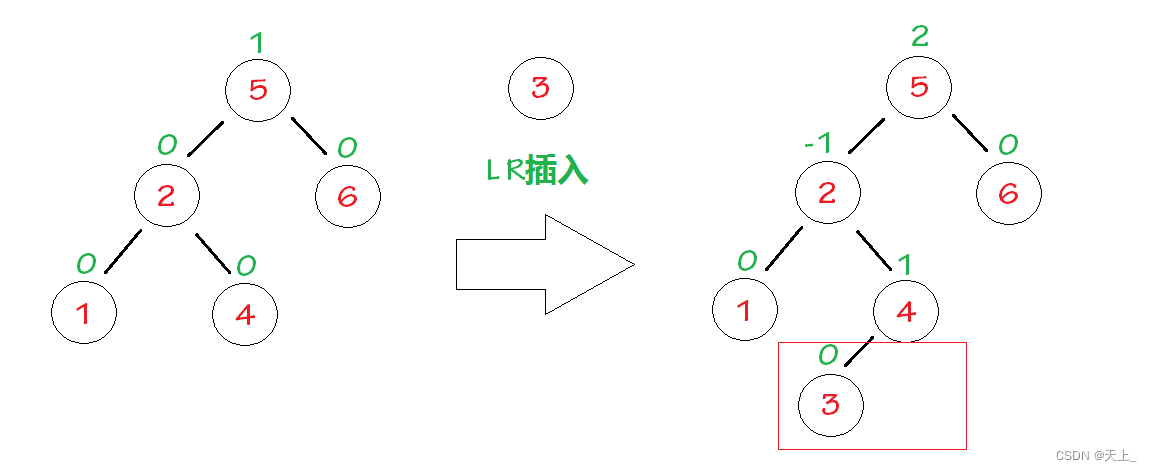
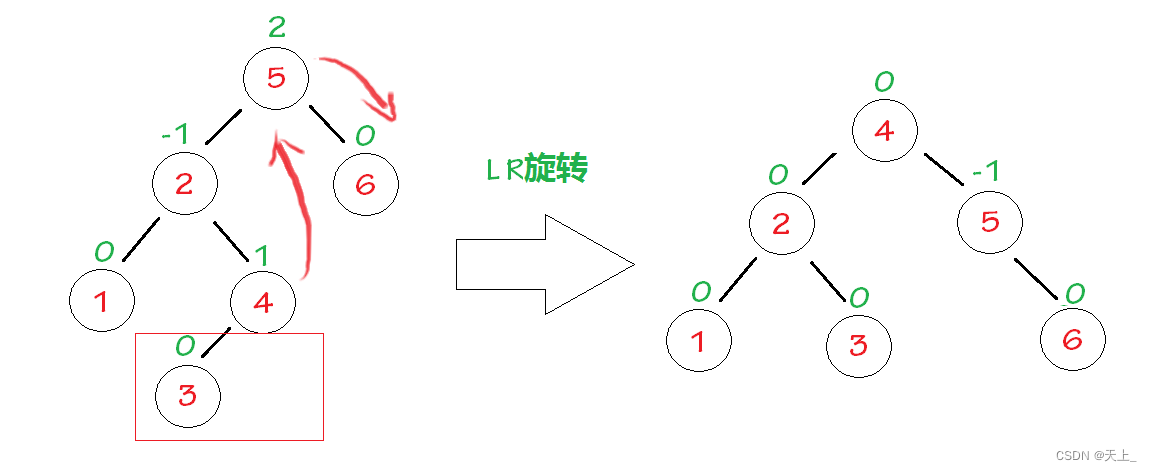
“发现者”是结点5,“麻烦结点”3在“发现者”左子树的右子树上,因而叫LR插入,需要进行LR旋转(左右双旋)。
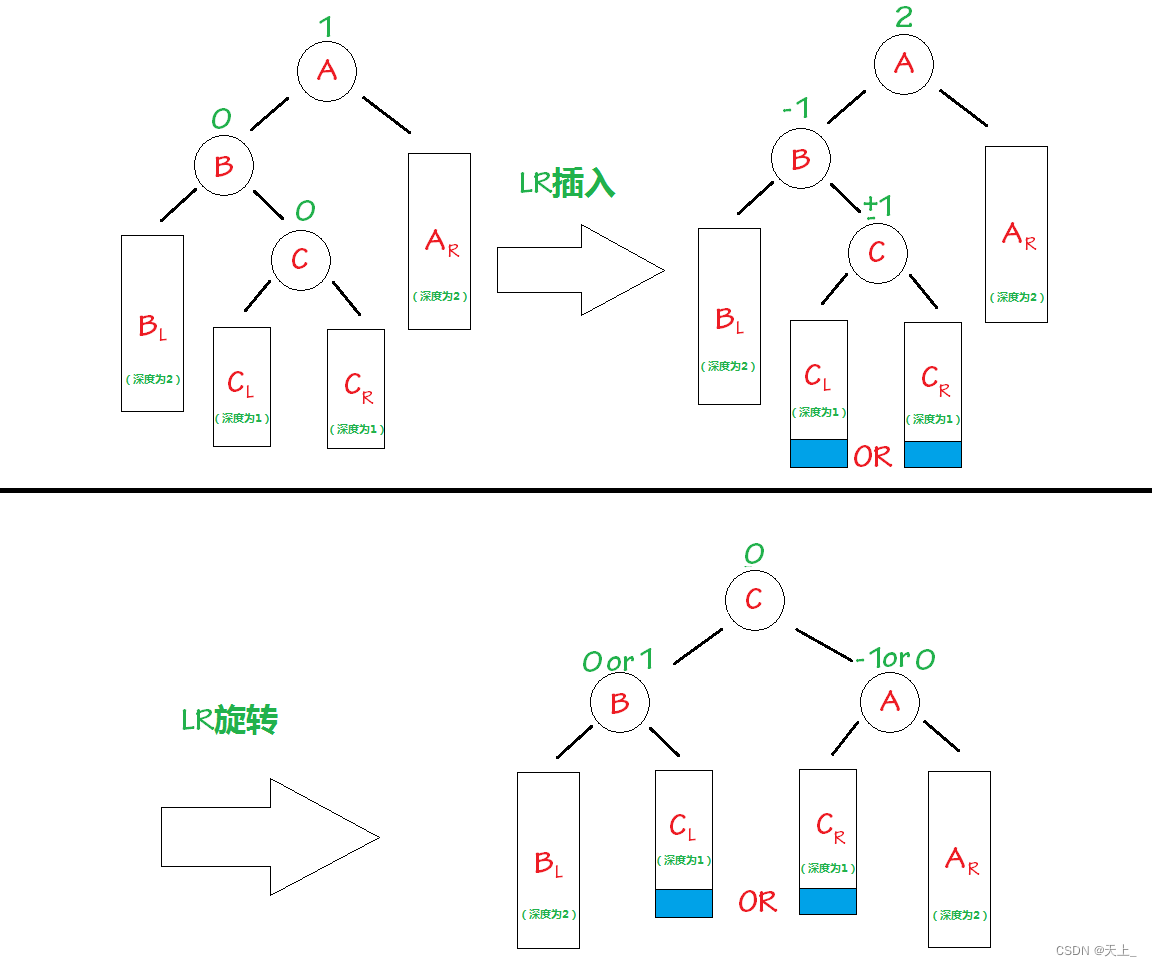
相关结点ABC旋转完之后,其余结点按原来的顺序接在B和A的左右子树中。
右左双旋
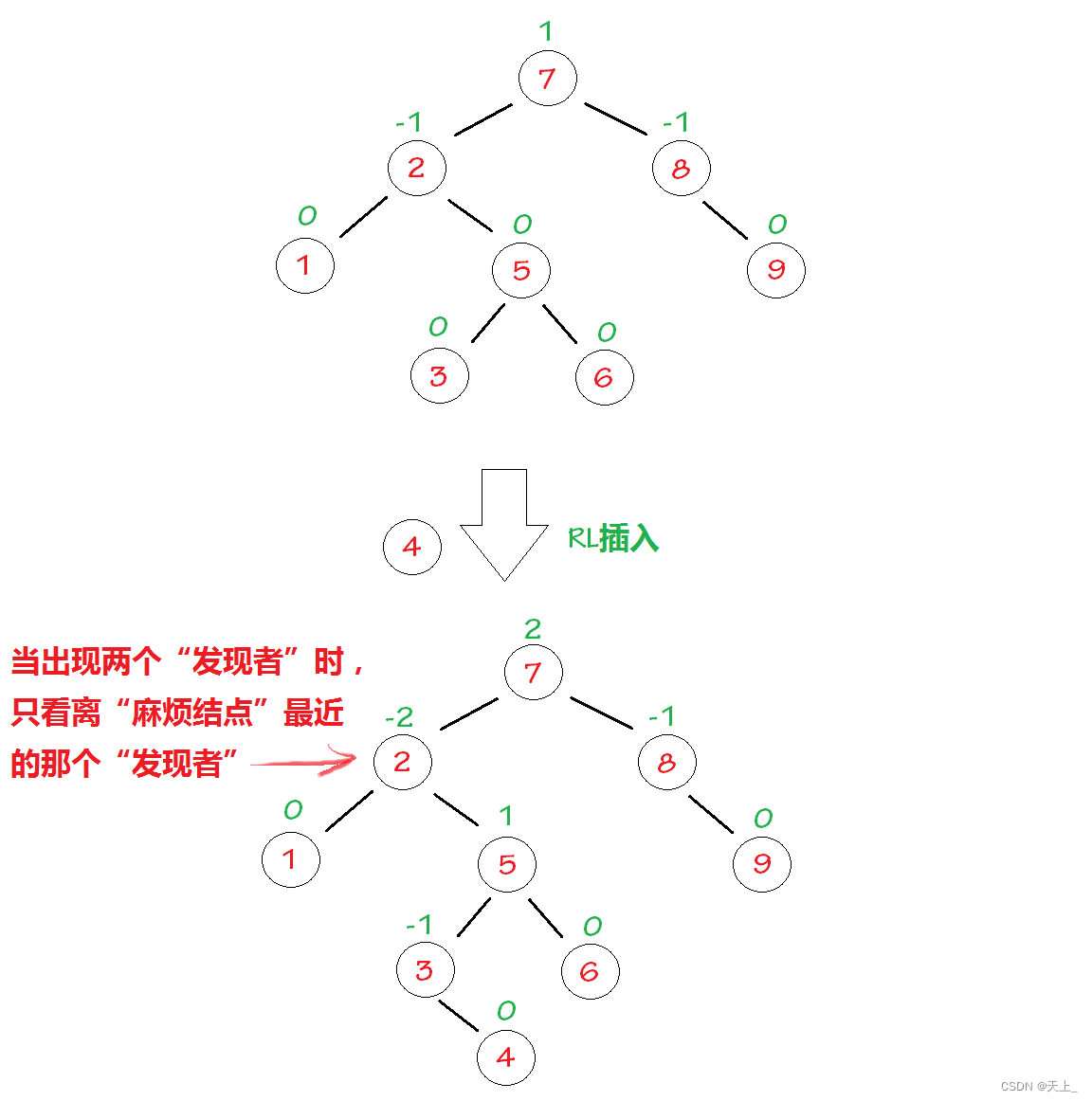
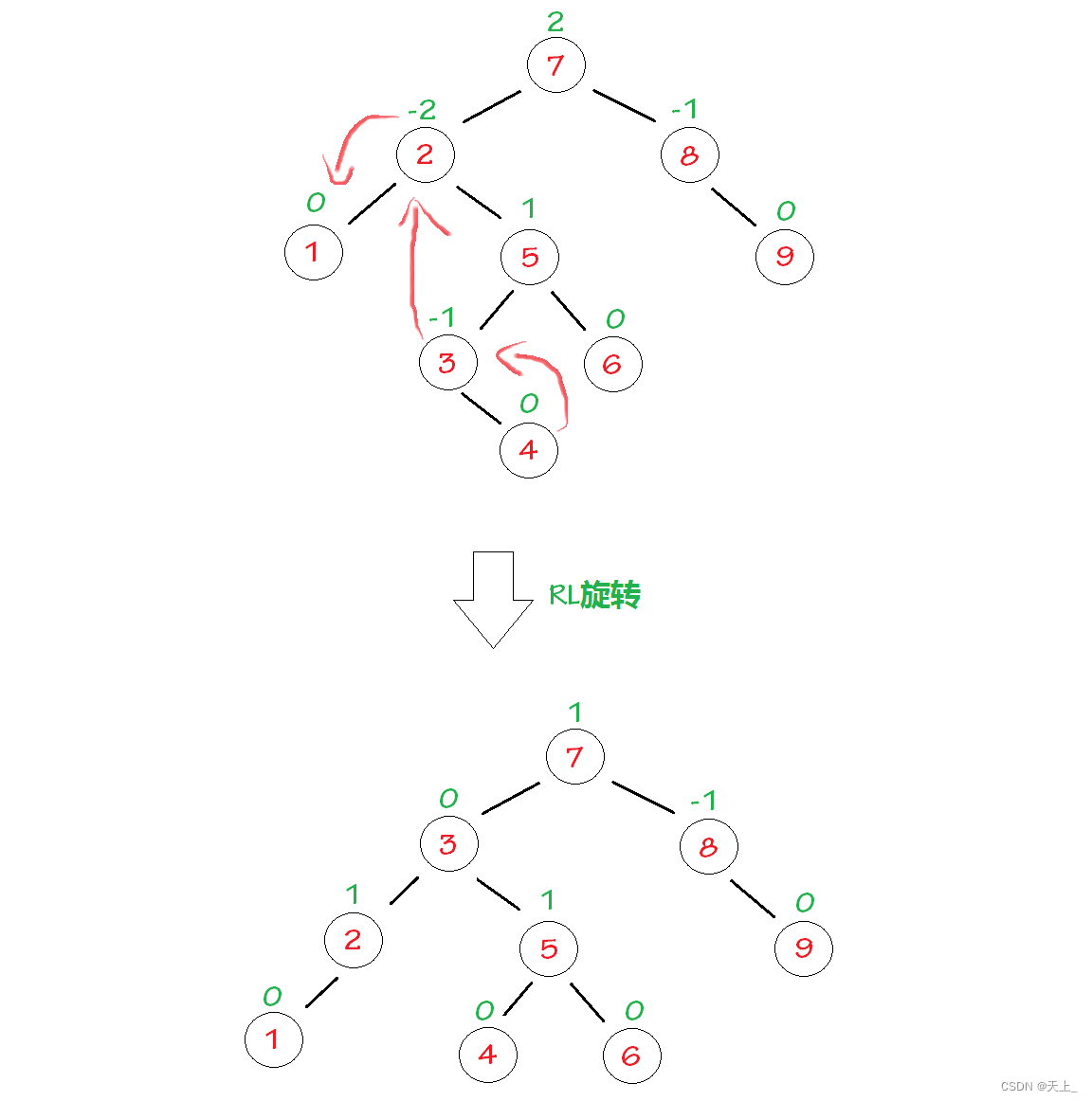
“发现者”是结点2,“麻烦结点”4在“发现者”右子树的左子树上,因而叫RL插入,需要进行RL旋转(右左双旋)。
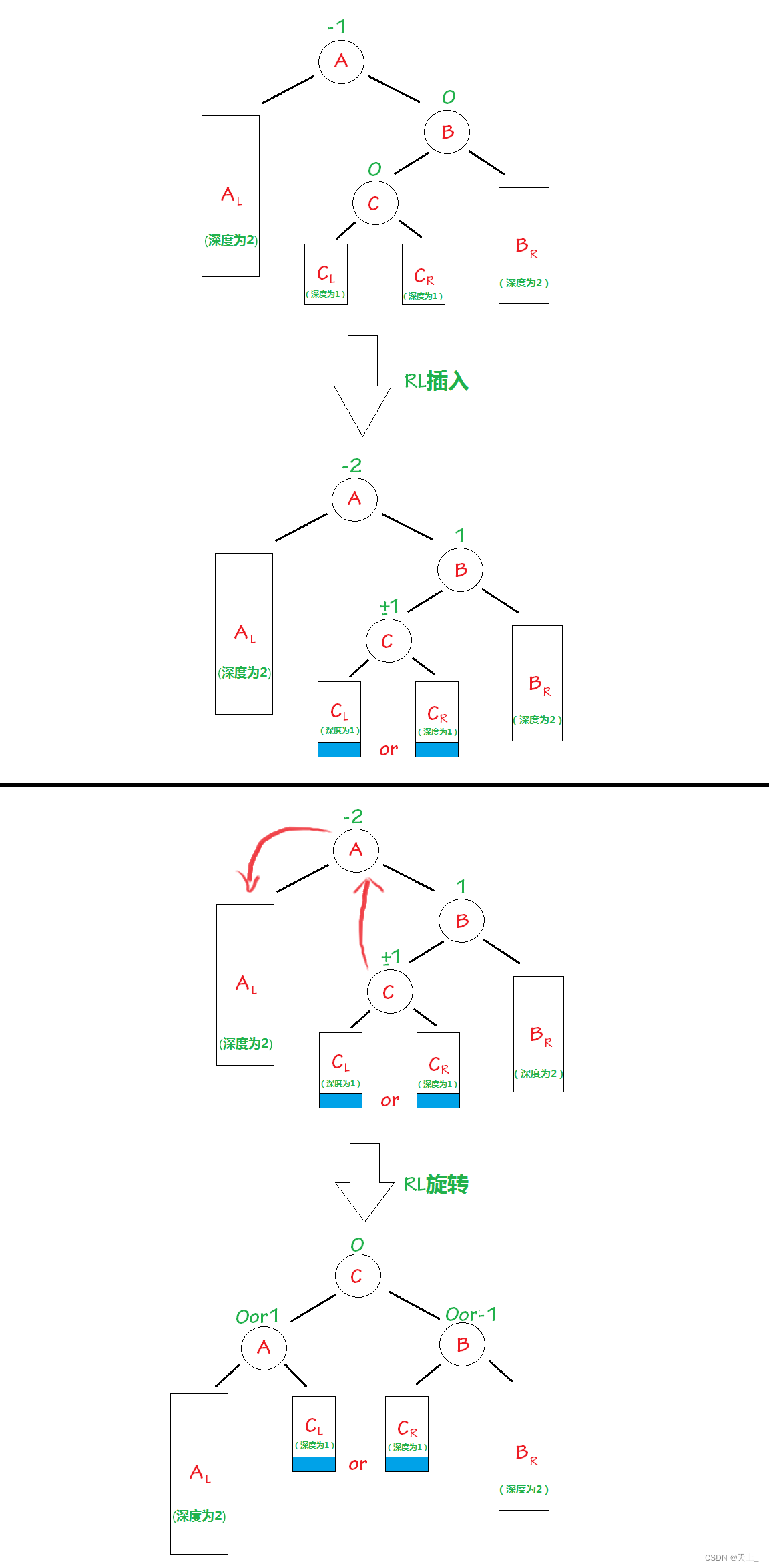
平衡因子的计算
有些时候,插入元素即便不需要调整结构,也可能需要重新计算一些平衡因子。
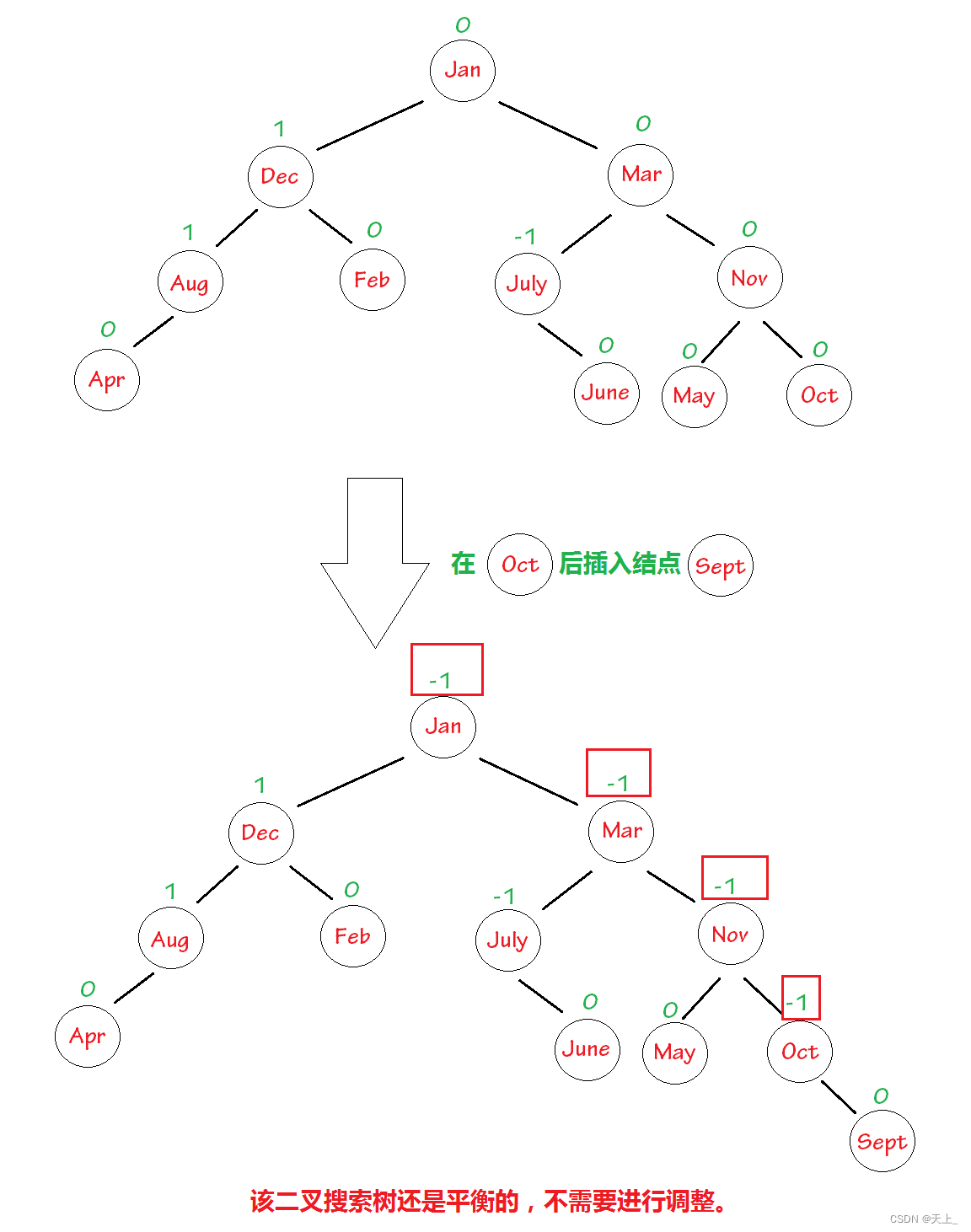
end
学习自:MOOC数据结构——陈越、何钦铭

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献9条内容
已为社区贡献9条内容







所有评论(0)