GitHub同步更新（已分类）：Data_Structure_And_Algorithm-Review

公众号：URLeisure 的复习仓库
公众号二维码见文末

以下是本篇文章正文内容，下面案例可供参考。

---

KMP 概述

• KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的。

• 因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。

• KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。

• 具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。

• KMP算法的时间复杂度$O(m+n)$ 。

KMP 分析

• 在上一篇文章中（模式匹配BF算法），BF 算法有点拖沓，完全没必要从 S 的每一个字符开始穷举每一种情况。

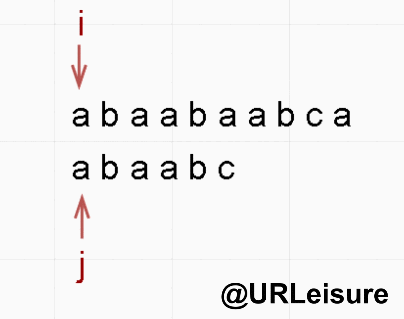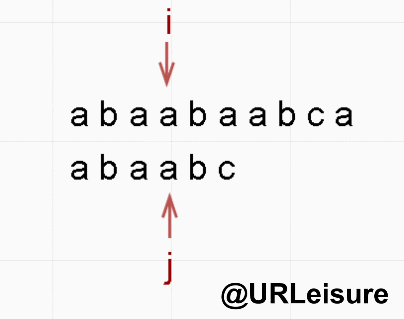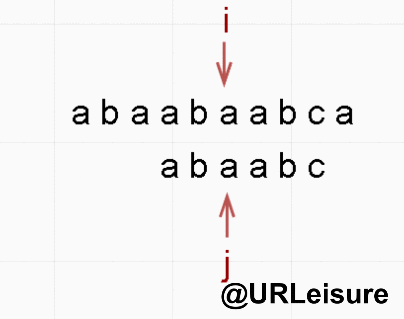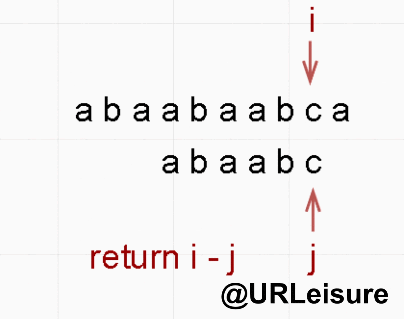
• 比如这一步：
  

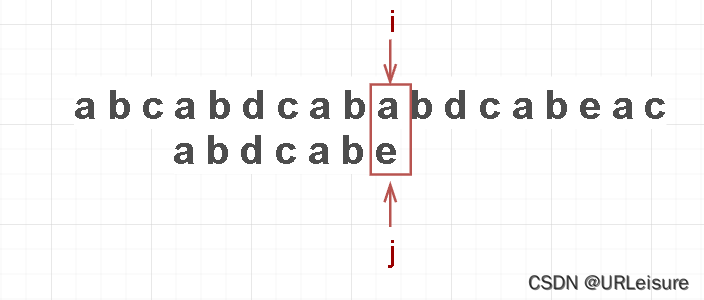
• 按照 BF 算法，i 回退到 i - j + 1 = 4 （从零开始），j 回退到 0：
  

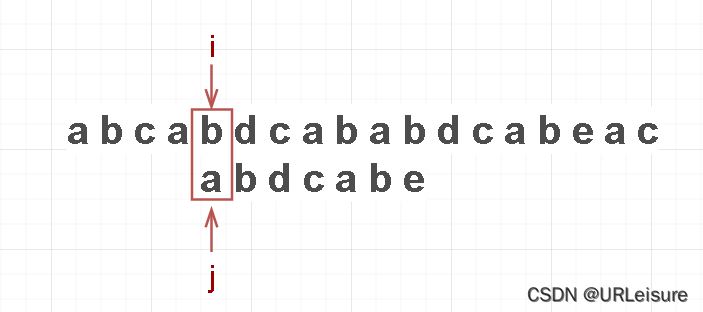
• 但通过观察，我们可以发现， i 不用回退，让 j 回退到 2 号索引位即可 （就像T向右滑动了一段距离）：

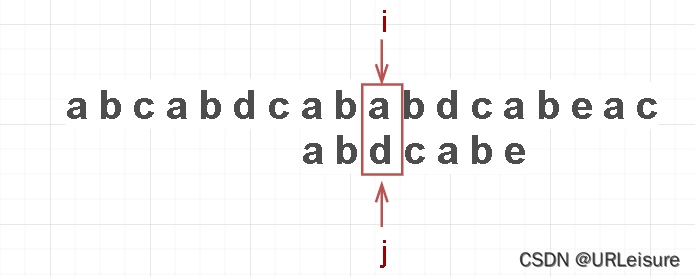
• 怎么观察出来的?

• i 前面两个字符和 T 的前面两个字符是相同的。

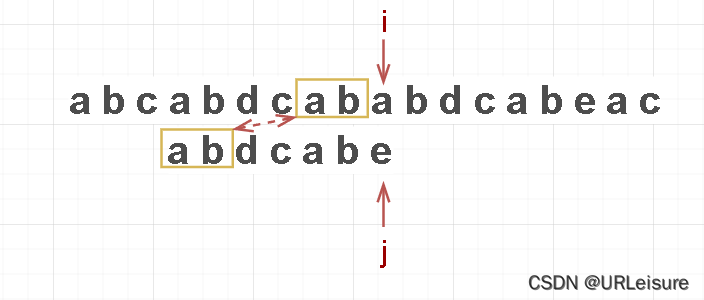
KMP next[ ]数组

1. 分析

• 如何判断 T 的开头和 i 指向的前面几个字符一样？

• 如果两个串直接比较的话也太麻烦了，又是指数级的操作。

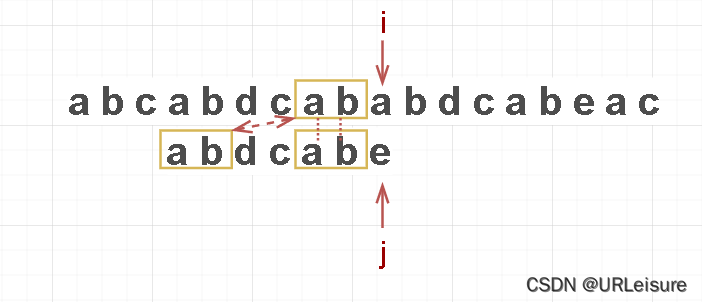
• 因为这两个串在 i、j 前已经比较过了，所以i 前面的字符和j 前面的字符是相等的，所以我们只比较 T 字符串自身就可以了。

• 假设 j 前所有字符为一个新的字符串 T`。

• 如果 T 的串长为 n ，我们只需要记录 n 个 T` 的公共前后缀长度即可。

• 这就转换成了一个新的问题，即记录 n 个 T` 的最长公共前后缀。

需要注意的是：

1. 前缀：从前向后取若干个字符。
2. 后缀：从后向前取若干个字符。
3. 前缀后缀不可取字符串本身。如果串长度为 n，则前缀和后缀的长度最多为 n - 1。

2. 创建

• 为了更好地体现 KMP 的优势和next[]数组的寻找方法，我们设 S = “abaabaabca”, T = “abaabc”。

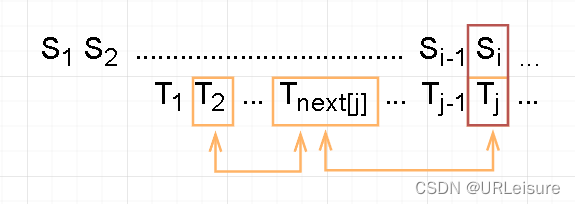
• 创建 next[ ] 数组，在T 和 S 进行比对时，当 S[ i ] != T[ j ] , i 不需要回退,而 j 回退到 next[ j ] ，再重新开始比较。

next[ j ] 的含义：

1. j 的回退位置。
2. T 串中前 j 个字符前后缀的最大匹配数。

• next[ j ] 的通用公式：

• 通过公式求得 next[ ] 数组。（注意：T` 是 j 前面的字符串，不包含第 j 个元素）

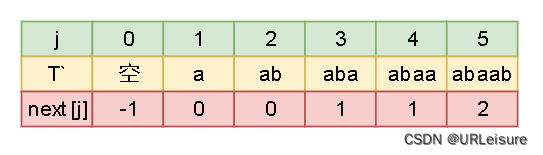
• 像 dp 问题。

假设，已知 next[ j ] = k 。next[ j+1 ] =

1. T_k = T_j ：next[ j+1 ] = k+1。即：下一个字符相等，那么公共长度就在上一次记录的基础上 +1。
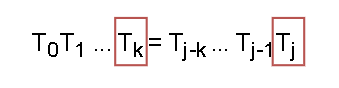
2. T_k ≠ T_j ：两者不相等时，我们又开始了这两个串的模式匹配（KMP里套小KMP，太（wu）妙（yu）了）。j 不动，k 回退到 next[ k ] （公共前后缀长度）。再重新比较，直到T_k = T_j 或者回退到 k = next[ 0 ] = -1 。

3.代码

c++代码如下（示例）：

void Get_next(char *T, int *next) {
    int j = 0;
    int k = -1;
    next[0] = -1;
    while(j < strlen(T) - 1) {
        if(k == -1 || T[j] == T[k]) {
            next[++j] = ++k;
        } else {
            k = next[k];//“小KMP”，模式匹配，回退到公共前后缀的下一个位置，再继续比较
        }
    }
}

java代码如下（示例）：

public static void get_next(String t, int[] next) {
    int j = 0;
    int k = -1;
    next[0] = -1;
  	while (j < t.length() - 1) {
        if (k == -1 || t.charAt(j) == t.charAt(k)) {
            next[++j] = ++k;
        } else {
            k = next[k];
        }
    }
}

KMP 完整代码

• 特别注意：在c++中，strlen() 等返回字符串长度的方法，返回值都是 ‘size_t’ (又名 ‘unsigned long’ )。

• 都是无符号整型，不能和负整型做比较!

• 我们的 j ，在有些情况是 -1，然后就会出 bug。

c++代码如下（示例）：

void Get_next(char *T, int *next) {
    int j = 0;
    int k = -1;
    next[0] = -1;
    while(j < strlen(T) - 1) {
        if(k == -1 || T[j] == T[k]) {
            next[++j] = ++k;
        } else {
            k = next[k];//“小KMP”，模式匹配，回退到公共前后缀的下一个位置，再继续比较
        }
    }
}

int Index_KMP(char *S, char *T, int *next) {
    int i = 0, j = 0;
    int lens = strlen(S);
    int lent = strlen(T);//一定要赋给 int 不然就是无符号的
    while (i < lens && j < lent) {
        if (j == -1 || S[i] == T[j]) {
            i++, j++;
        } else {
            j = next[j];
        }
    }
    if (j == strlen(T)) {
        return i - j;
    }
    return -1;
}

java代码如下（示例）：

public static void get_next(String t, int[] next) {
    int j = 0;
    int k = -1;
    next[0] = -1;
  	while (j < t.length() - 1) {
        if (k == -1 || t.charAt(j) == t.charAt(k)) {
            next[++j] = ++k;
        } else {
            k = next[k];
        }
    }
}

public static int index_KMP(String s, String t, int[] next) {
    int i = 0, j = 0;
	while (i < s.length() && j < t.length()) {
       	if (j == -1 || s.charAt(i) == t.charAt(j)) {
            i++;
            j++;
        } else {
            j = next[j];
        }
    }
    if (j == t.length()) {
        return i - j;
    }
    return -1;
}

KMP 优化

• 当 S[ i ] ≠ T [ j ] 时，j 回退到 next[ j ]。

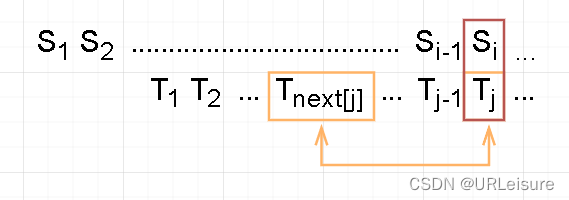
• 但就在这时，当T[ j ] = T[ next[ j ] ] ，就是一步没有意义的回退。

• 因为跳转之后还要进行 S[ i ] 和 T[ j ] 的比较，T[ j ] 的值没变，肯定还是不相等，肯定还要往前跳。

那如何减少这些无效的跳转？

• 在制作 next[ ] 数组时，只要遇到相等的字符，就直接存上一次的值就可以了。

c++代码如下（示例）：

void Get_next(char *T, int *next) {
    int j = 0;
    int k = -1;
    next[0] = -1;
    while (j < strlen(T) - 1) {
        if (k == -1 || T[j] == T[k]) {
            next[++j] = ++k;
            if (T[j] == T[k]) {
                next[j] = next[k];
            }
        } else {
            k = next[k];
        }
    }
}

java代码如下（示例）：

public static void get_next(String t, int[] next) {
    int j = 0;
    int k = -1;
    next[0] = -1;
	while (j < t.length() - 1) {
        if (k == -1 || t.charAt(j) == t.charAt(k)) {
            next[++j] = ++k;
            if (t.charAt(j) == t.charAt(k)) {
                next[j] = next[k];
            }
        } else {
            k = next[k];
        }
    }
}

KMP 时间复杂度分析

1. 在 S 、T 比较时（ Index_KMP() 方法），i 不回退，当 S[ i ] ≠ T[ j ] 时，j 回退到 next[ j ]，重新开始比较。最坏的情况就是扫描整个S串，时间复杂度为 $O(n)$。
2. 计算 next[ ] 数组时，需要扫描整个 T 串，时间复杂度为 $O(m)$。

• KMP的优化并没有降阶，因此复杂度仍为 $O(n+m)$。

BF 算法与 KMP 算法动态图解对比

• 同样的，S 、T 串。S = “abaabaabca”, T = “abaabc”。

1. BF 算法：
   
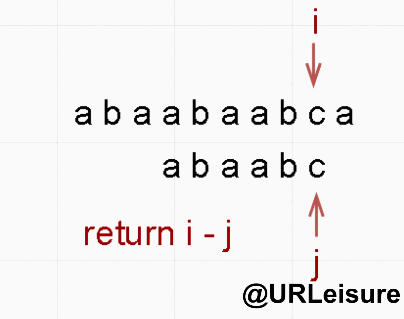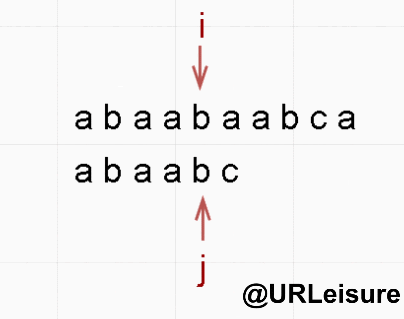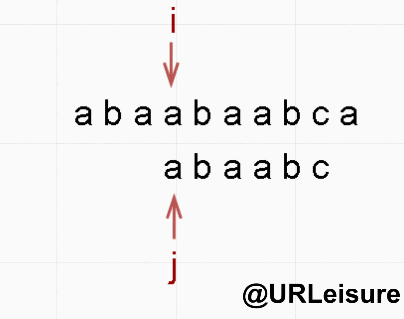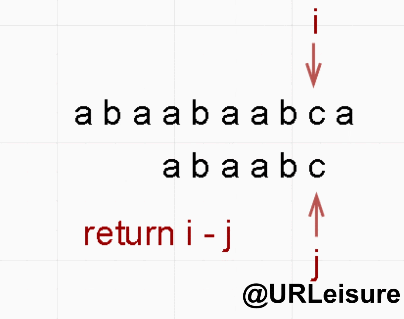
2. KMP 算法：
   

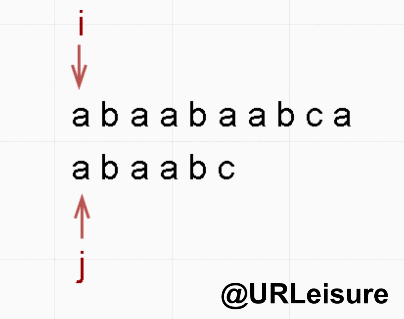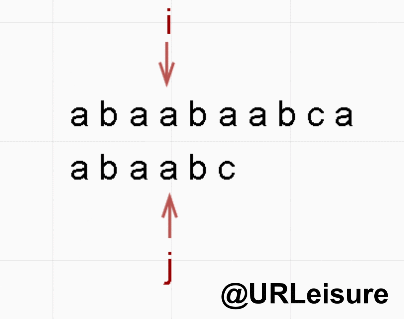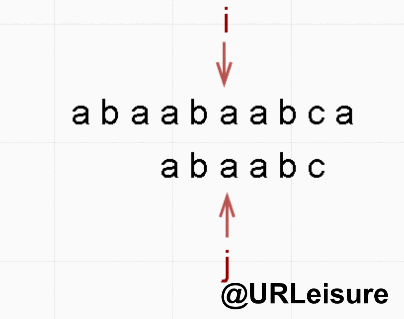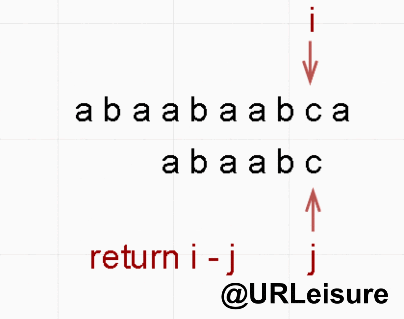
• 通过动态图我们可以看出，KMP 算法明显比 BF 算法节省很多时间。

---

关注公众号，感受不同的阅读体验

下期预告：特殊矩阵的存储