目录

1.折半查找

2.插值查找

（1）原理部分

（2）代码实现 

3.斐波那契查找

（1）原理部分

（2）代码实现

1.折半查找

使用C语言实现查找

上面链接已经给出了折半查找的非递归过程，下面主要给出递归实现折半查找：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

#define maxn 100

int n;
int array[maxn];

void init(){
	for(int i=0;i<n;i++){
		array[i]=0;
	}
}

int findMid(int array[],int low,int high,int key){
	if(low>high){
		return -1;
	}
	int mid=(low+high)/2;
	if(key<array[mid]){
		findMid(array,low,mid-1,key);
	}else if(key>array[mid]){
		findMid(array,mid+1,high,key);
	}else{
		return mid;
	}
}

int main(){
	printf("请输入元数个数: ");
	scanf("%d",&n);
	init();
	printf("请输入元数: \n");
	for(int i=0;i<n;i++){
		scanf("%d",&array[i]);
	}
	int key;
	printf("请输入要查找的元素: ");
	scanf("%d",&key);
	int mid=findMid(array,0,n-1,key);
	if(mid!=-1){
		printf("查找元素的位置为: %d\n",mid+1);
	}else{
		printf("查找失败\n");
	}
	return 0;
}

2.插值查找

（1）原理部分

插值查找类似于二分查找，不同的是插值查找根据给定值key来确定进行比较的关键字array[i]的查找方法。

主要公式：

• mid=low+(key-array[low])/(array[high]-array[low])*(high-low);

主要注意事项：

• 对于数据量较大，关键字分布比较均匀的有序查找表来说，采用插值查找，速度比较快。
• 当关键字分布不均匀的话，插值查找的效率不一定比折半查找好。

（2）代码实现 

实现方法：

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

#define maxn 100

int n;
int array[maxn];

void init(){
	for(int i=0;i<n;i++){
		array[i]=0;
	}
}

int findMid(int array[],int low,int high,int key){
	if(low>high||key<array[low]||key>array[high]){
		return -1;
	}
	int mid=low+(key-array[low])/(array[high]-array[low])*(high-low);
	if(key<array[mid]){
		findMid(array,low,mid-1,key);
	}else if(key>array[mid]){
		findMid(array,mid+1,high,key);
	}else{
		return mid;
	}
}

int main(){
	printf("请输入元数个数: ");
	scanf("%d",&n);
	init();
	printf("请输入元数: \n");
	for(int i=0;i<n;i++){
		scanf("%d",&array[i]);
	}
	int key;
	printf("请输入要查找的元素: ");
	scanf("%d",&key);
	int mid=findMid(array,0,n-1,key);
	if(mid!=-1){
		printf("查找元素的位置为: %d\n",mid+1);
	}else{
		printf("查找失败\n");
	}
	return 0;
}

 

3.斐波那契查找

（1）原理部分

对于斐波那契数列大家应该都非常的熟悉：

• 比如：{1,1,2,3,5,8,13,21,34,55}这是一个斐波那契数列；
• 计算的公式：f(1)=1,f(2)=1;f(k)=f(k-1)+f(k-2);
• 对公式进行变换一下：
  • f(k)-1=[f(k-1)-1]+[f(k-2)-1]+1;
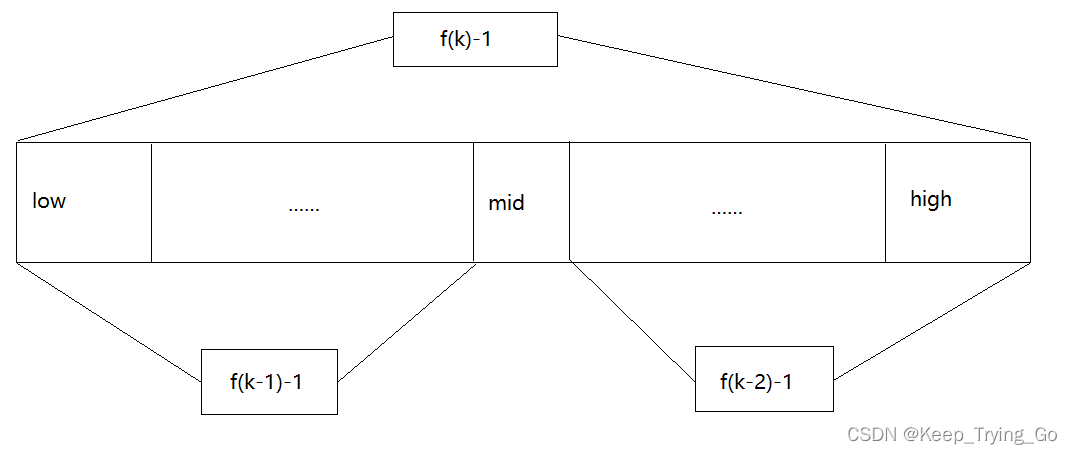
  • 说明：主要顺序表的长度为f(k)-1，则可以将该表分成f(k-1)-1和f(k-2)-1两段，从而中间的位置mid=low+f(k-1)-1;
  • 类似的：每一子段都可以使用相同的方法进行分割；
  • 注意：并不是元素的个数n总是等于f(k)-1的，所需要将大于顺序表array的那一部分进行填补，使用array[high]的值进行填补。最后要使得f(k)-1的大于等于n即可。

 

（2）代码实现

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

#define maxn 100

int n;
int array[maxn];
int f[maxn];

void init(){
	for(int i=0;i<maxn;i++){
		array[i]=0;
		f[i]=0;
	}
}
//计算斐波那契数列 
void fib(){
	f[0]=1;
	f[1]=1;
	for(int i=2;i<maxn-5;i++){
		f[i]=f[i-1]+f[i-2];
	}
}

int findMid(int array[],int low,int high,int key){
	//当f(k)-1的值小于n的时候，进行填充
	int k=0;
	while(f[k]-1<high){
		k++;
	} 
	int tmp[maxn];
	for(int i=0;i<n;i++){
		tmp[i]=array[i];
	}
	//进行填充 
	for(int i=high;i<f[k];i++){
		tmp[i]=array[high];
	}
	while(low<=high){
		int mid=low+f[k-1]-1;
		if(key<tmp[mid]){
			high=mid-1;
			//f(k-1)-1
			k-=1;
		}else if(key>tmp[mid]){
			low=mid+1;
			//f(k-2)-1 
			k-=2;
		}else{
			if(low<=high){
				return mid;
			}else{
				return high;
			}
		}
	}
	return -1;
}

int main(){
	printf("请输入元数个数: ");
	scanf("%d",&n);
	init();
	fib();
	printf("请输入元数: \n");
	for(int i=0;i<n;i++){
		scanf("%d",&array[i]);
	}
	int key;
	printf("请输入要查找的元素: ");
	scanf("%d",&key);
	int mid=findMid(array,0,n-1,key);
	if(mid!=-1){
		printf("查找元素的位置为: %d\n",mid+1);
	}else{
		printf("查找失败\n");
	}
	return 0;
}