十大经典排序算法——插入排序
将列表分为已排序部分和未排序部分。初始时,已排序部分只包含第一个元素,未排序部分包含剩余元素。最坏情况:O(n²),当列表是逆序时,每次插入都需要移动所有已排序元素。最好情况:O(n),当列表已经有序时,只需遍历一次列表。O(1),插入排序是原地排序算法,不需要额外的存储空间。:将该元素与已排序部分的元素从后向前依次比较,找到合适的位置插入。:重复上述步骤,直到未排序部分为空,列表完全有序。取出未
插入排序(Insertion Sort)是一种简单直观的排序算法,它的工作原理类似于整理扑克牌。插入排序通过构建有序序列,对于未排序的数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理解的了,因为只要打过扑克牌的人都应该能够秒懂。插入排序和冒泡排序一样,也有一种优化算法,叫做拆半插入。
一、算法步骤
-
初始化:将列表分为已排序部分和未排序部分。初始时,已排序部分只包含第一个元素,未排序部分包含剩余元素。
-
选择元素:从未排序部分中取出第一个元素。
-
插入到已排序部分:将该元素与已排序部分的元素从后向前依次比较,找到合适的位置插入。
-
重复步骤:重复上述步骤,直到未排序部分为空,列表完全有序。
二、动图演示
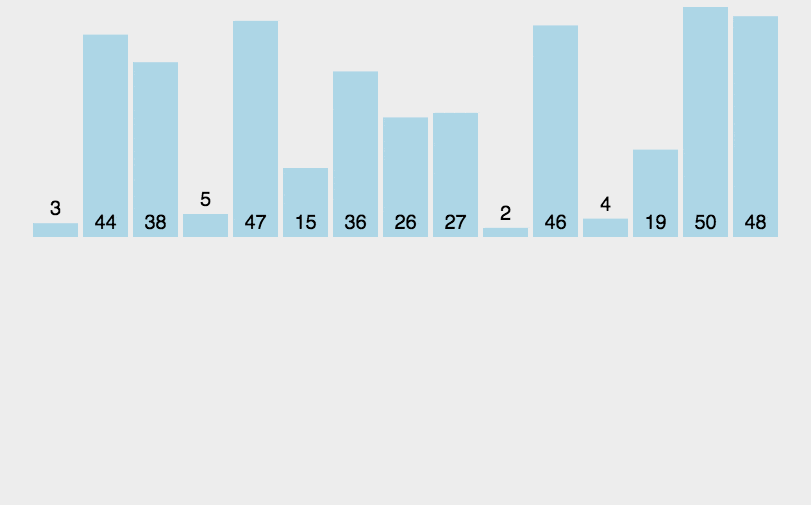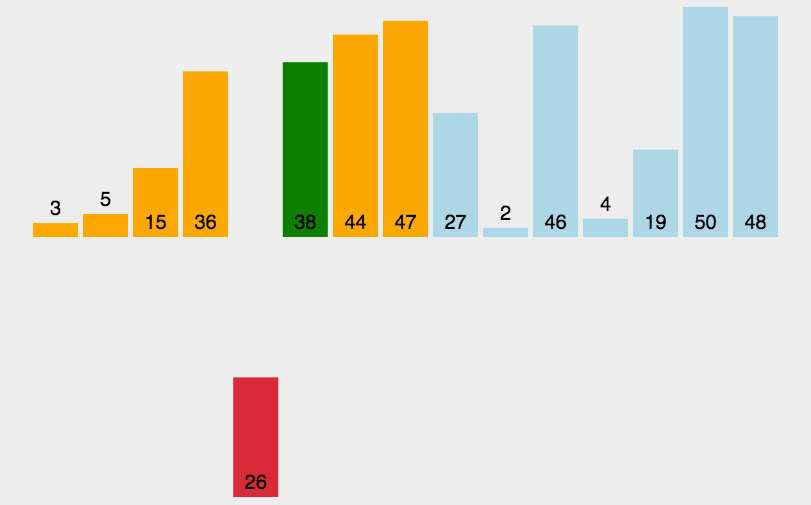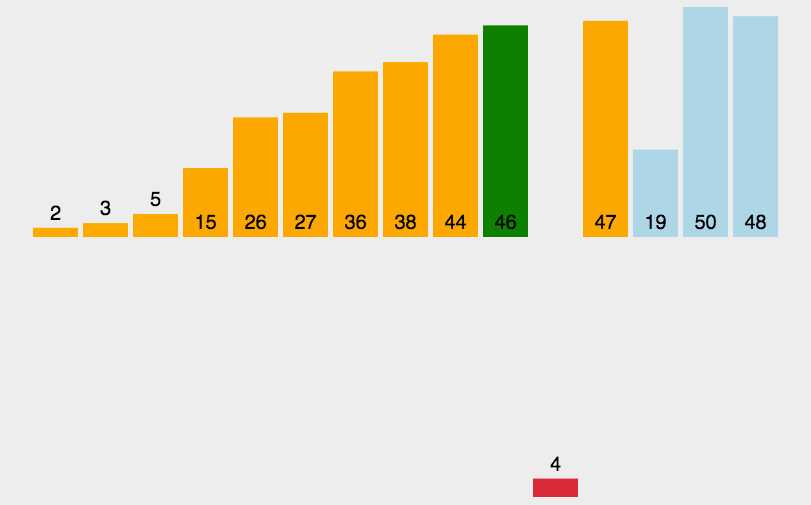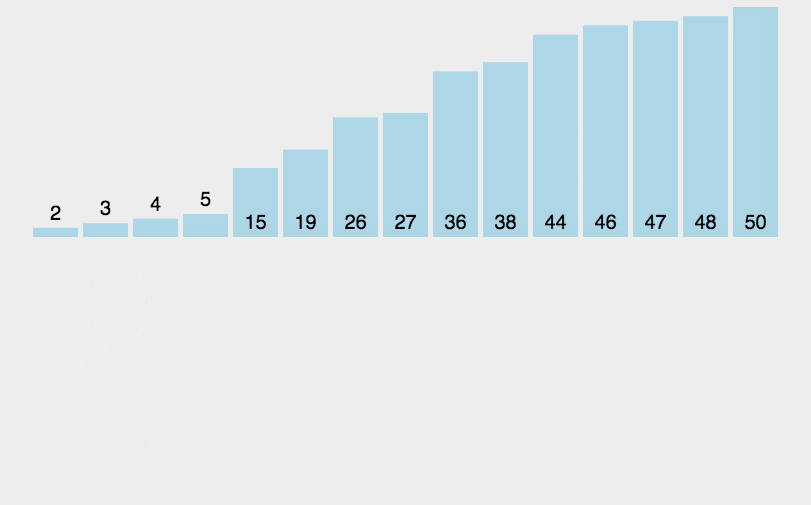
假设有一个待排序的列表 [5, 2, 4, 6, 1, 3],插入排序的过程如下:
-
初始状态:
-
已排序部分:
[5]。 -
未排序部分:
[2, 4, 6, 1, 3]。
-
-
第一轮:
-
取出未排序部分的第一个元素
2。 -
将
2与已排序部分的5比较,2 < 5,插入到5前面。 -
列表变为
[2, 5, 4, 6, 1, 3]。 -
已排序部分:
[2, 5],未排序部分:[4, 6, 1, 3]。
-
-
第二轮:
-
取出未排序部分的第一个元素
4。 -
将
4与已排序部分的5比较,4 < 5,继续与2比较,4 > 2,插入到2和5之间。 -
列表变为
[2, 4, 5, 6, 1, 3]。 -
已排序部分:
[2, 4, 5],未排序部分:[6, 1, 3]。
-
-
第三轮:
-
取出未排序部分的第一个元素
6。 -
将
6与已排序部分的5比较,6 > 5,直接插入到末尾。 -
列表变为
[2, 4, 5, 6, 1, 3]。 -
已排序部分:
[2, 4, 5, 6],未排序部分:[1, 3]。
-
-
第四轮:
-
取出未排序部分的第一个元素
1。 -
将
1与已排序部分的6比较,1 < 6,继续与5、4、2比较,1是最小的,插入到最前面。 -
列表变为
[1, 2, 4, 5, 6, 3]。 -
已排序部分:
[1, 2, 4, 5, 6],未排序部分:[3]。
-
-
第五轮:
-
取出未排序部分的第一个元素
3。 -
将
3与已排序部分的6比较,3 < 6,继续与5、4、2比较,3 > 2,插入到2和4之间。 -
列表变为
[1, 2, 3, 4, 5, 6]。 -
已排序部分:
[1, 2, 3, 4, 5, 6],未排序部分为空。
-
三、代码实现
实例
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i] # 取出未排序部分的第一个元素
j = i - 1
# 将 key 插入到已排序部分的正确位置
while j >= 0 and key < arr[j]:
arr[j + 1] = arr[j] # 向后移动元素
j -= 1
arr[j + 1] = key # 插入 key
return arr
# 示例
arr = [5, 2, 4, 6, 1, 3]
sorted_arr = insertion_sort(arr)
print(sorted_arr) # 输出: [1, 2, 3, 4, 5, 6]JavaScript
function insertionSort(arr) {
var len = arr.length;
var preIndex, current;
for (var i = 1; i < len; i++) {
preIndex = i - 1;
current = arr[i];
while(preIndex >= 0 && arr[preIndex] > current) {
arr[preIndex+1] = arr[preIndex];
preIndex--;
}
arr[preIndex+1] = current;
}
return arr;
}Python
def insertionSort(arr):
for i in range(len(arr)):
preIndex = i-1
current = arr[i]
while preIndex >= 0 and arr[preIndex] > current:
arr[preIndex+1] = arr[preIndex]
preIndex-=1
arr[preIndex+1] = current
return arrGo
func insertionSort(arr []int) []int {
for i := range arr {
preIndex := i - 1
current := arr[i]
for preIndex >= 0 && arr[preIndex] > current {
arr[preIndex+1] = arr[preIndex]
preIndex -= 1
}
arr[preIndex+1] = current
}
return arr
}Java
public class InsertSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for (int i = 1; i < arr.length; i++) {
// 记录要插入的数据
int tmp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
while (j > 0 && tmp < arr[j - 1]) {
arr[j] = arr[j - 1];
j--;
}
// 存在比其小的数,插入
if (j != i) {
arr[j] = tmp;
}
}
return arr;
}
}PHP
function insertionSort($arr)
{
$len = count($arr);
for ($i = 1; $i < $len; $i++) {
$preIndex = $i - 1;
$current = $arr[$i];
while($preIndex >= 0 && $arr[$preIndex] > $current) {
$arr[$preIndex+1] = $arr[$preIndex];
$preIndex--;
}
$arr[$preIndex+1] = $current;
}
return $arr;
}C
void insertion_sort(int arr[], int len){
int i,j,key;
for (i=1;i<len;i++){
key = arr[i];
j=i-1;
while((j>=0) && (arr[j]>key)) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
}C++
void insertion_sort(int arr[],int len){
for(int i=1;i<len;i++){
int key=arr[i];
int j=i-1;
while((j>=0) && (key<arr[j])){
arr[j+1]=arr[j];
j--;
}
arr[j+1]=key;
}
}C#
public static void InsertSort(int[] array)
{
for(int i = 1;i < array.length;i++)
{
int temp = array[i];
for(int j = i - 1;j >= 0;j--)
{
if(array[j] > temp)
{
array[j + 1] = array[j];
array[j] = temp;
}
else
break;
}
}
}Rust
/// 插入排序
/// 0 ,..., j, i, ... n
/// 0 ,..., j: 为有序序列,j = i ,..., n
/// i ,..., n: 为无序序列 i = 1,2,3,4,5,...n
/// 从无序序列中的第一个元素(target)与有序序列从右到左进行比较,
/// 当target < array[j], target与array[j]交换,
/// 否则退出循环
/// 此时从无序序列的第一个元素已经插入到有序序列中
fn insert_sort<T:Ord + Debug>(array: &mut [T]) {
for i in 1..array.len() {
for j in (0..i).rev() {
if array[j + 1] < array[j] {
array.swap(j + 1, j);
} else {
break;
}
}
}
}Swift
for i in 1..<arr.endIndex {
let temp = arr[i]
for j in (0..<i).reversed() {
if arr[j] > temp {
arr.swapAt(j, j+1)
}
}
}Lua
-- 插入排序
function insert_sort(tab)
len = maxn_ex(tab)
for i=1,len-1 do
local j = i+1
while( j > 1 ) do
if(tab[j] < tab[j-1]) then
tab[j],tab[j-1] = tab[j-1],tab[j]
end
j = j -1
end
end
return tab
end四、复杂度
1、时间复杂度
最坏情况:O(n²),当列表是逆序时,每次插入都需要移动所有已排序元素。
最好情况:O(n),当列表已经有序时,只需遍历一次列表。
平均情况:O(n²)。
2、空间复杂度
O(1),插入排序是原地排序算法,不需要额外的存储空间。
五、优缺点
-
优点:
-
实现简单,代码易于理解。
-
对小规模数据或基本有序的数据效率较高。
-
原地排序,不需要额外的存储空间。
-
稳定排序算法(相同元素的相对顺序不会改变)。
-
-
缺点:
-
时间复杂度较高,不适合大规模数据集。
-

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容







所有评论(0)