关键路径

关键路径是求「工程上时间最短的问题」的方法

阅读本文前请先了解

拓扑排序

拓扑排序主要解决「工程是否能顺序进行」的问题，关键路径在拓扑排序的基础上解决「工程最短时间的问题」。

一、工程最短时间

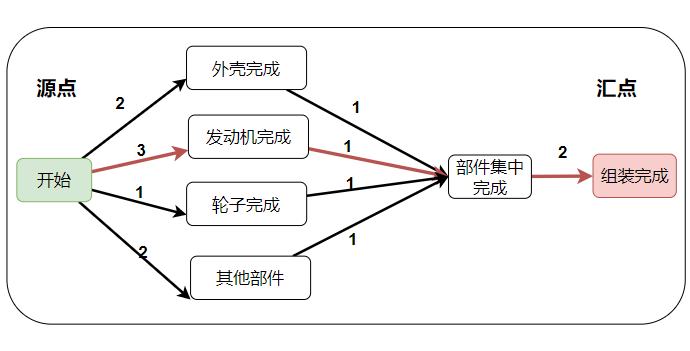
工程时间最短的问题：

按照工厂上图生产一辆汽车，外壳、发动机、轮子和其他部件可以同时建造。

（1）求组装完成最短需要多少时间？

（2）如何缩短最短时间？

答案：

（1）

因为所有部件可以同时建造，所以只要最长时间的「发动机」不建造完毕集中部件就无法进行。所以：「工程最短时间」就是通向汇点的和 最长的权重。（最长权重的路径也叫做「关键路径」）

上图 开始 -> 发动机完成 -> 部件集中完成 -> 组装完成 就是最长权重，组装完成最短用时 6

（2）

关键路径性质：缩短关键路径上的时间就能缩短最短时间（但是缩短的同时关键路径会动态发生变化，比如发动机建造时间 <= 2 ，继续缩短发动机建造时间就没用了）

二、AOE （Activity On Edge）网络

找出最长权重的路径就是关键路径。所以边必须有权重。（没权重咋算？？）

我们要在「拓扑排序」AOV 网的基础上介绍 AOE 网，区别如下

• AOV（Activity On Vertex）：活动在顶点上，边没有权重
• AOE（Activity On Edge）：活动在边上，边有权重

定义如下：

• 边（Edge）称之为「活动」（比如造轮子）

• 顶点（Vertex）称之为「事件」（比如说轮子完成）

三、关键路基算法

3.1 关键路径算法原理

我们如何求出关键路径？

我们举个例子：

小明有 2 个小时的作业，回家一共有 4 个小时做作业的时间。他可以选择一开始就做，或者因为「ddl 综合征」最后 2 小时才开始做。此时「做作业最早的时间」和「做作业的最晚时间」是不等的。

老师知道小明的情况后将小明的作业增加到了 4 个小时的量，小明做作业的时间还是 4 个小时。小明只能回家就开始做作业才能做完。此时「做作业最早的时间」和「做作业的最晚时间」是相等的。

「做作业最早的时间」和「做作业的最晚时间」是相等的说明：如果做作业的时间延误，将会导致整个工期延误，做作业的时间缩短，整个工期的最短时间就会缩短。

我们将「做作业」抽象为「活动」Activity，「作业完成」抽象为「事件」Event

关键路径定义：活动的最早发生时间和最晚发生时间相等的路径就是关键路径

求关键路径我们只需要求出「活动最早发生时间」和「活动最晚发生时间」即可。

3.2 关键路径算法

（1）参数定义

求关键路径我们只需要求出「活动最早发生时间」和「活动最晚发生时间」即可。

但是在 AOE 图中，「活动」就是向量边，求向量边一般是困难的，我们可以借助顶点来求边。

参数定义如下：

• etv（Earliest Time of Vertex）：顶点最早发生时间，也就是「事件最早发生时间」
• ltv（Lastest Time of Vertex）：顶点最晚发生时间，也就是「事件最晚发生时间」
• ete（Earliest Time of Edge）：边最早发生时间，也就是「活动最早发生时间」
• lte（Lastest Time of Edge）：边最晚发生时间，也就是「活动最晚发生时间」

我们通过 etv 求 ete，ltv 求 lte

（2）算法步骤

步骤如下：（结合代码理解）

• 通过拓扑排序求出 etv「事件最早发生时间」

  e t v [ j ] = m a x { e t v ( i ) + w e i g h t < i , j > } etv[j] = max\{etv(i) + weight<i,j>\} etv[j]=max{etv(i)+weight<i,j>}

• 通过「反向推导」求出 ltv「事件最晚发生时间」

  l t v [ i ] = m a x { e t v ( j ) − w e i g h t < i , j > } ltv[i] = max\{etv(j) - weight<i,j>\} ltv[i]=max{etv(j)−weight<i,j>}

• 通过 etv 求出 ete「活动最早发生时间」

  活动最早发生时间等于 $from$（箭头开始方向的事件最早发动时间）

• 通过 ltv 求出 lte「活动最晚发生时间」

  活动最晚发生时间等于 $to-weight$（箭头结束方向的事件发生时间 - 权重）

• 通过 lte - ete 求出关键路径

四、代码

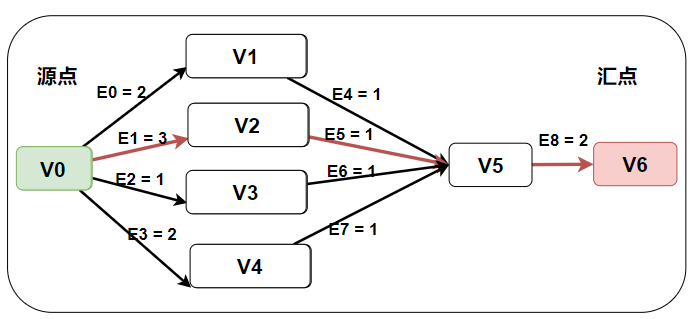
示例如下图：

public class CriticalPath {
    /** 边 */
    static class Edge{
        /** 权重 */
        int weight;
        /** 出度指向的点 */
        int toVertex;
        Edge next;
        public Edge(int weight, int toVertex, Edge next) {
            this.weight = weight;
            this.toVertex = toVertex;
            this.next = next;
        }
    }
    /** 顶点 */
    static class Vertex{
        /** 入度 数量 */
        int inNumber;
        /** 顶点信息 */
       Integer data;
        /** 第一条边 */
        Edge firstEdge;
        public Vertex(int inNumber, Integer data, Edge firstEdge) {
            this.inNumber = inNumber;
            this.data = data;
            this.firstEdge = firstEdge;
        }
    }
    static void criticalPath(List<Vertex> graph){
        //顶点数量
        int length = graph.size();
        //边数量
        int numOfEdges = 0;
        for (Vertex vertex : graph) {
            Edge edge = vertex.firstEdge;
            while (edge!=null){
                numOfEdges ++;
                edge = edge.next;
            }
        }
        //事件最早发生时间
        int[] etv = new int[length];
        //事件最晚发生时间
        int[] ltv = new int[length];
        //活动最早发生时间
        int[] ete = new int[numOfEdges];
        //活动最晚发生时间
        int[] lte = new int[numOfEdges];
        //1. 通过拓扑排序求 etv 「事件最早发生时间」
        //etvStack 用于储存拓扑排序后的顺序
        Stack<Vertex> etvStack = new Stack<>();
        //stack 用于拓扑排序
        Stack<Vertex> stack = new Stack<>();
        for (Vertex vertex : graph) {
            if (vertex.inNumber == 0){
                stack.push(vertex);
            }
        }
        while (!stack.isEmpty()){
            Vertex pop = stack.pop();
            //储存拓扑排序后的结构
            etvStack.push(pop);
            //遍历出度
            Edge edge = pop.firstEdge;
            while (edge != null){
                Vertex vertex = graph.get(edge.toVertex);
                vertex.inNumber --;
                if (vertex.inNumber == 0){
                    stack.push(vertex);
                }
                //赋值更大的距离给 etv
                if (etv[pop.data] + edge.weight > etv[edge.toVertex]){
                    etv[edge.toVertex] = etv[pop.data] + edge.weight;
                }
                edge = edge.next;
            }
        }
        //2.通过 etv 反向推导求出 ltv「事件最晚发生时间」
        System.out.println("====etv====");
        for (int i = 0; i < etv.length; i++) {
            System.out.print("V"+i +" = "+etv[i]+" ");
        }
        System.out.println();

        //初始化 ltv
        Integer endVertex = etvStack.peek().data;
        for (int i = 0; i < ltv.length; i++) {
            ltv[i] = etv[endVertex];
        }
        while (!etvStack.isEmpty()) {
            Vertex pop = etvStack.pop();
            Edge edge = pop.firstEdge;
            while (edge != null) {
                //赋值更小的距离给 ltv
                if (ltv[pop.data] > ltv[edge.toVertex] - edge.weight) {
                    ltv[pop.data] = ltv[edge.toVertex] - edge.weight;
                }
                edge = edge.next;
            }
        }
        System.out.println("====ltv====");
        for (int i = 0; i < ltv.length; i++) {
            System.out.print("V"+i +" = "+ltv[i]+" ");
        }
        System.out.println();
        //3. 通过 etv 求 ete
        int index = 0;
        for (Vertex vertex : graph) {
            Edge edge = vertex.firstEdge;
            while (edge != null){
                ete[index++] = etv[vertex.data];
                edge = edge.next;
            }
        }
        System.out.println("====ete====");
        for (int i = 0; i < ete.length; i++) {
            System.out.print("E"+i +" = "+ete[i]+" ");
        }
        System.out.println();
        //4. 通过 ltv 求 lte
        index = 0;
        for (Vertex vertex : graph) {
            Edge edge = vertex.firstEdge;
            while (edge != null){
                lte[index++] = ltv[edge.toVertex] - edge.weight;
                edge = edge.next;
            }
        }
        System.out.println("====lte====");
        for (int i = 0; i < lte.length; i++) {
            System.out.print("E"+i +" = "+lte[i]+" ");
        }
        System.out.println();
        //5. 用 lte - ete 求关键路径 
        System.out.println("====关键路径====");
        for (int i = 0; i < ete.length; i++) {
            if (lte[i] - ete[i] == 0) {
                System.out.print("E"+i+" ");
            }
        }
        return ;
    }

    /** 测试 */
    public static void main(String[] args) {
        char[] vertices = new char[]{'A','B','C','D','E','F','G'};
        Edge e3 = new Edge(2, 4, null);
        Edge e2 = new Edge(1, 3, e3);
        Edge e1 = new Edge(3, 2, e2);
        Edge e0 = new Edge(2, 1, e1);
        Edge e4 = new Edge(1, 5, null);
        Edge e5 = new Edge(1, 5, null);
        Edge e6 = new Edge(1, 5, null);
        Edge e7 = new Edge(1, 5, null);
        Edge e8 = new Edge(2, 6, null);
        Vertex a = new Vertex(0, 0, e0);
        Vertex b = new Vertex(1, 1, e4);
        Vertex c = new Vertex(1, 2, e5);
        Vertex d = new Vertex(1, 3, e6);
        Vertex e = new Vertex(1, 4, e7);
        Vertex f = new Vertex(4, 5, e8);
        Vertex g = new Vertex(1, 6, null);
        ArrayList<Vertex> graph = new ArrayList<>();
        graph.add(a);
        graph.add(b);
        graph.add(c);
        graph.add(d);
        graph.add(e);
        graph.add(f);
        graph.add(g);
        criticalPath(graph);
    }
}

结果：

====etv====
V0 = 0 V1 = 2 V2 = 3 V3 = 1 V4 = 2 V5 = 4 V6 = 6 
====ltv====
V0 = 0 V1 = 3 V2 = 3 V3 = 3 V4 = 3 V5 = 4 V6 = 6 
====ete====
E0 = 0 E1 = 0 E2 = 0 E3 = 0 E4 = 2 E5 = 3 E6 = 1 E7 = 2 E8 = 4 
====lte====
E0 = 1 E1 = 0 E2 = 2 E3 = 1 E4 = 3 E5 = 3 E6 = 3 E7 = 3 E8 = 4 
====关键路径====
E1 E5 E8