十大经典排序算法——堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。

—————————————————

936人浏览 · 2025-07-22 12:20:13

————————————————— · 2025-07-22 12:20:13 发布

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

一、算法步骤

创建一个堆 H[0……n-1]；
把堆首（最大值）和堆尾互换；
把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
重复步骤 2，直到堆的尺寸为 1。

二、动图演示

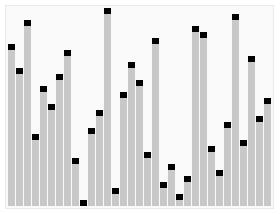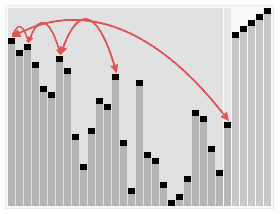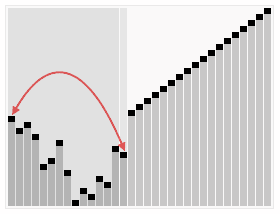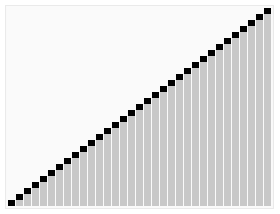
假设有一个待排序的列表 [4, 10, 3, 5, 1]，堆排序的过程如下：

构建最大堆：
- 初始列表：[4, 10, 3, 5, 1]。
- 从最后一个非叶子节点开始，逐步调整堆：
  - 调整节点 5：[4, 10, 3, 5, 1]（无需调整）。
  - 调整节点 10：[4, 10, 3, 5, 1]（无需调整）。
  - 调整节点 4：[10, 5, 3, 4, 1]。
- 最终最大堆：[10, 5, 3, 4, 1]。
交换堆顶元素：
- 将堆顶元素 10 与最后一个元素 1 交换，列表变为 [1, 5, 3, 4, 10]。
- 堆的大小减 1，已排序部分为 [10]。
调整堆：
- 对新的堆顶元素 1 进行下沉操作：
  - 比较 1 和其子节点 5、3，将 1 与 5 交换。
  - 列表变为 [5, 1, 3, 4, 10]。
  - 继续比较 1 和其子节点 4，将 1 与 4 交换。
  - 列表变为 [5, 4, 3, 1, 10]。
- 调整后的堆：[5, 4, 3, 1]。
重复步骤：
- 将堆顶元素 5 与最后一个元素 1 交换，列表变为 [1, 4, 3, 5, 10]。
- 堆的大小减 1，已排序部分为 [5, 10]。
- 对新的堆顶元素 1 进行下沉操作：
  - 比较 1 和其子节点 4、3，将 1 与 4 交换。
  - 列表变为 [4, 1, 3, 5, 10]。
- 调整后的堆：[4, 1, 3]。
继续重复：
- 将堆顶元素 4 与最后一个元素 3 交换，列表变为 [3, 1, 4, 5, 10]。
- 堆的大小减 1，已排序部分为 [4, 5, 10]。
- 对新的堆顶元素 3 进行下沉操作：
  - 比较 3 和其子节点 1，无需交换。
- 调整后的堆：[3, 1]。
最终步骤：
- 将堆顶元素 3 与最后一个元素 1 交换，列表变为 [1, 3, 4, 5, 10]。
- 堆的大小减 1，已排序部分为 [3, 4, 5, 10]。
- 堆的大小为 1，排序完成。

三、代码实现

实例

def heapify(arr, n, i):
    # 找到当前节点、左子节点和右子节点中的最大值
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[left] > arr[largest]:
        largest = left
    if right < n and arr[right] > arr[largest]:
        largest = right

    # 如果最大值不是当前节点，交换并继续调整
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def heap_sort(arr):
    n = len(arr)

    # 构建最大堆
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # 逐个取出堆顶元素并调整堆
    for i in range(n - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]  # 交换堆顶元素和最后一个元素
        heapify(arr, i, 0)  # 调整堆

    return arr

# 示例
arr = [4, 10, 3, 5, 1]
sorted_arr = heap_sort(arr)
print(sorted_arr)  # 输出: [1, 3, 4, 5, 10]

JavaScript

var len;    // 因为声明的多个函数都需要数据长度，所以把len设置成为全局变量

function buildMaxHeap(arr) {   // 建立大顶堆
    len = arr.length;
    for (var i = Math.floor(len/2); i >= 0; i--) {
        heapify(arr, i);
    }
}

function heapify(arr, i) {     // 堆调整
    var left = 2 * i + 1,
        right = 2 * i + 2,
        largest = i;

    if (left < len && arr[left] > arr[largest]) {
        largest = left;
    }

    if (right < len && arr[right] > arr[largest]) {
        largest = right;
    }

    if (largest != i) {
        swap(arr, i, largest);
        heapify(arr, largest);
    }
}

function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

function heapSort(arr) {
    buildMaxHeap(arr);

    for (var i = arr.length-1; i > 0; i--) {
        swap(arr, 0, i);
        len--;
        heapify(arr, 0);
    }
    return arr;
}

Python

def buildMaxHeap(arr):
    import math
    for i in range(math.floor(len(arr)/2),-1,-1):
        heapify(arr,i)

def heapify(arr, i):
    left = 2*i+1
    right = 2*i+2
    largest = i
    if left < arrLen and arr[left] > arr[largest]:
        largest = left
    if right < arrLen and arr[right] > arr[largest]:
        largest = right

    if largest != i:
        swap(arr, i, largest)
        heapify(arr, largest)

def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]

def heapSort(arr):
    global arrLen
    arrLen = len(arr)
    buildMaxHeap(arr)
    for i in range(len(arr)-1,0,-1):
        swap(arr,0,i)
        arrLen -=1
        heapify(arr, 0)
    return arr

Go

func heapSort(arr []int) []int {
        arrLen := len(arr)
        buildMaxHeap(arr, arrLen)
        for i := arrLen - 1; i >= 0; i-- {
                swap(arr, 0, i)
                arrLen -= 1
                heapify(arr, 0, arrLen)
        }
        return arr
}

func buildMaxHeap(arr []int, arrLen int) {
        for i := arrLen / 2; i >= 0; i-- {
                heapify(arr, i, arrLen)
        }
}

func heapify(arr []int, i, arrLen int) {
        left := 2*i + 1
        right := 2*i + 2
        largest := i
        if left < arrLen && arr[left] > arr[largest] {
                largest = left
        }
        if right < arrLen && arr[right] > arr[largest] {
                largest = right
        }
        if largest != i {
                swap(arr, i, largest)
                heapify(arr, largest, arrLen)
        }
}

func swap(arr []int, i, j int) {
        arr[i], arr[j] = arr[j], arr[i]
}

Java

public class HeapSort implements IArraySort {

    @Override
    public int[] sort(int[] sourceArray) throws Exception {
        // 对 arr 进行拷贝，不改变参数内容
        int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);

        int len = arr.length;

        buildMaxHeap(arr, len);

        for (int i = len - 1; i > 0; i--) {
            swap(arr, 0, i);
            len--;
            heapify(arr, 0, len);
        }
        return arr;
    }

    private void buildMaxHeap(int[] arr, int len) {
        for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
            heapify(arr, i, len);
        }
    }

    private void heapify(int[] arr, int i, int len) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;

        if (left < len && arr[left] > arr[largest]) {
            largest = left;
        }

        if (right < len && arr[right] > arr[largest]) {
            largest = right;
        }

        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, largest, len);
        }
    }

    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

}

PHP

function buildMaxHeap(&$arr)
{
    global $len;
    for ($i = floor($len/2); $i >= 0; $i--) {
        heapify($arr, $i);
    }
}

function heapify(&$arr, $i)
{
    global $len;
    $left = 2 * $i + 1;
    $right = 2 * $i + 2;
    $largest = $i;

    if ($left < $len && $arr[$left] > $arr[$largest]) {
        $largest = $left;
    }

    if ($right < $len && $arr[$right] > $arr[$largest]) {
        $largest = $right;
    }

    if ($largest != $i) {
        swap($arr, $i, $largest);
        heapify($arr, $largest);
    }
}

function swap(&$arr, $i, $j)
{
    $temp = $arr[$i];
    $arr[$i] = $arr[$j];
    $arr[$j] = $temp;
}

function heapSort($arr) {
    global $len;
    $len = count($arr);
    buildMaxHeap($arr);
    for ($i = count($arr) - 1; $i > 0; $i--) {
        swap($arr, 0, $i);
        $len--;
        heapify($arr, 0);
    }
    return $arr;
}

C

#include <stdio.h>
#include <stdlib.h>

void swap(int *a, int *b) {
    int temp = *b;
    *b = *a;
    *a = temp;
}

void max_heapify(int arr[], int start, int end) {
    // 建立父節點指標和子節點指標
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { // 若子節點指標在範圍內才做比較
        if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小，選擇最大的
            son++;
        if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢，直接跳出函數
            return;
        else { // 否則交換父子內容再繼續子節點和孫節點比較
            swap(&arr[dad], &arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}

void heap_sort(int arr[], int len) {
    int i;
    // 初始化，i從最後一個父節點開始調整
    for (i = len / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    // 先將第一個元素和已排好元素前一位做交換，再重新調整，直到排序完畢
    for (i = len - 1; i > 0; i--) {
        swap(&arr[0], &arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}

int main() {
    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
    int len = (int) sizeof(arr) / sizeof(*arr);
    heap_sort(arr, len);
    int i;
    for (i = 0; i < len; i++)
        printf("%d ", arr[i]);
    printf("\n");
    return 0;
}

C++

#include <iostream>
#include <algorithm>
using namespace std;

void max_heapify(int arr[], int start, int end) {
    // 建立父節點指標和子節點指標
    int dad = start;
    int son = dad * 2 + 1;
    while (son <= end) { // 若子節點指標在範圍內才做比較
        if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小，選擇最大的
            son++;
        if (arr[dad] > arr[son]) // 如果父節點大於子節點代表調整完畢，直接跳出函數
            return;
        else { // 否則交換父子內容再繼續子節點和孫節點比較
            swap(arr[dad], arr[son]);
            dad = son;
            son = dad * 2 + 1;
        }
    }
}

void heap_sort(int arr[], int len) {
    // 初始化，i從最後一個父節點開始調整
    for (int i = len / 2 - 1; i >= 0; i--)
        max_heapify(arr, i, len - 1);
    // 先將第一個元素和已经排好的元素前一位做交換，再從新調整(刚调整的元素之前的元素)，直到排序完畢
    for (int i = len - 1; i > 0; i--) {
        swap(arr[0], arr[i]);
        max_heapify(arr, 0, i - 1);
    }
}

int main() {
    int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
    int len = (int) sizeof(arr) / sizeof(*arr);
    heap_sort(arr, len);
    for (int i = 0; i < len; i++)
        cout << arr[i] << ' ';
    cout << endl;
    return 0;
}

C#

/// <summary>
/// 堆排序
/// </summary>
/// <param name="arr">待排序数组</param>
static void HeapSort(int[] arr)
{
    int vCount = arr.Length;
    int[] tempKey = new int[vCount + 1];
    // 元素索引从1开始
    for (int i = 0; i < vCount; i++)
    {
        tempKey[i + 1] = arr[i];
    }
    // 初始数据建堆（从含最后一个结点的子树开始构建，依次向前，形成整个二叉堆）
    for (int i = vCount / 2; i >= 1; i--)
    {
        Restore(tempKey, i, vCount);
    }
    // 不断输出堆顶元素、重构堆，进行排序
    for (int i = vCount; i > 1; i--)
    {
        int temp = tempKey[i];
        tempKey[i] = tempKey[1];
        tempKey[1] = temp;
        Restore(tempKey, 1, i - 1);
    }
    //排序结果
    for (int i = 0; i < vCount; i++)
    {
        arr[i] = tempKey[i + 1];
    }
}
/// <summary>
/// 二叉堆的重构（针对于已构建好的二叉堆首尾互换之后的重构）
/// </summary>
/// <param name="arr"></param>
/// <param name="rootNode">根结点j</param>
/// <param name="nodeCount">结点数</param>
static void Restore(int[] arr, int rootNode, int nodeCount)
{
    while (rootNode <= nodeCount / 2) // 保证根结点有子树
    {
        //找出左右儿子的最大值
        int m = (2 * rootNode + 1 <= nodeCount && arr[2 * rootNode + 1] > arr[2 * rootNode]) ? 2 * rootNode + 1 : 2 * rootNode;
        if (arr[m] > arr[rootNode])
        {
            int temp = arr[m];
            arr[m] = arr[rootNode];
            arr[rootNode] = temp;
            rootNode = m;
        }
        else
        {
            break;
        }
    }
}

四、复杂度

1、时间复杂度

构建最大堆：O(n)。
每次调整堆：O(log n)，总共需要调整 n-1 次。
总时间复杂度：O(n log n)。

2、空间复杂度

O(1)，堆排序是原地排序算法，不需要额外的存储空间。

五、优缺点

优点：
- 优点：
  - 时间复杂度稳定为 O(n log n)，适合大规模数据。
  - 原地排序，不需要额外的存储空间。
缺点：
- 不稳定排序算法（可能改变相同元素的相对顺序）。
- 对于小规模数据，性能可能不如插入排序等简单算法。

六、适用场景

大规模数据集的排序。
对性能要求较高的场景。
适合内存排序（不适合外部排序）。

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。