【数据结构与算法 经典例题】判断一颗二叉树是否是平衡二叉树
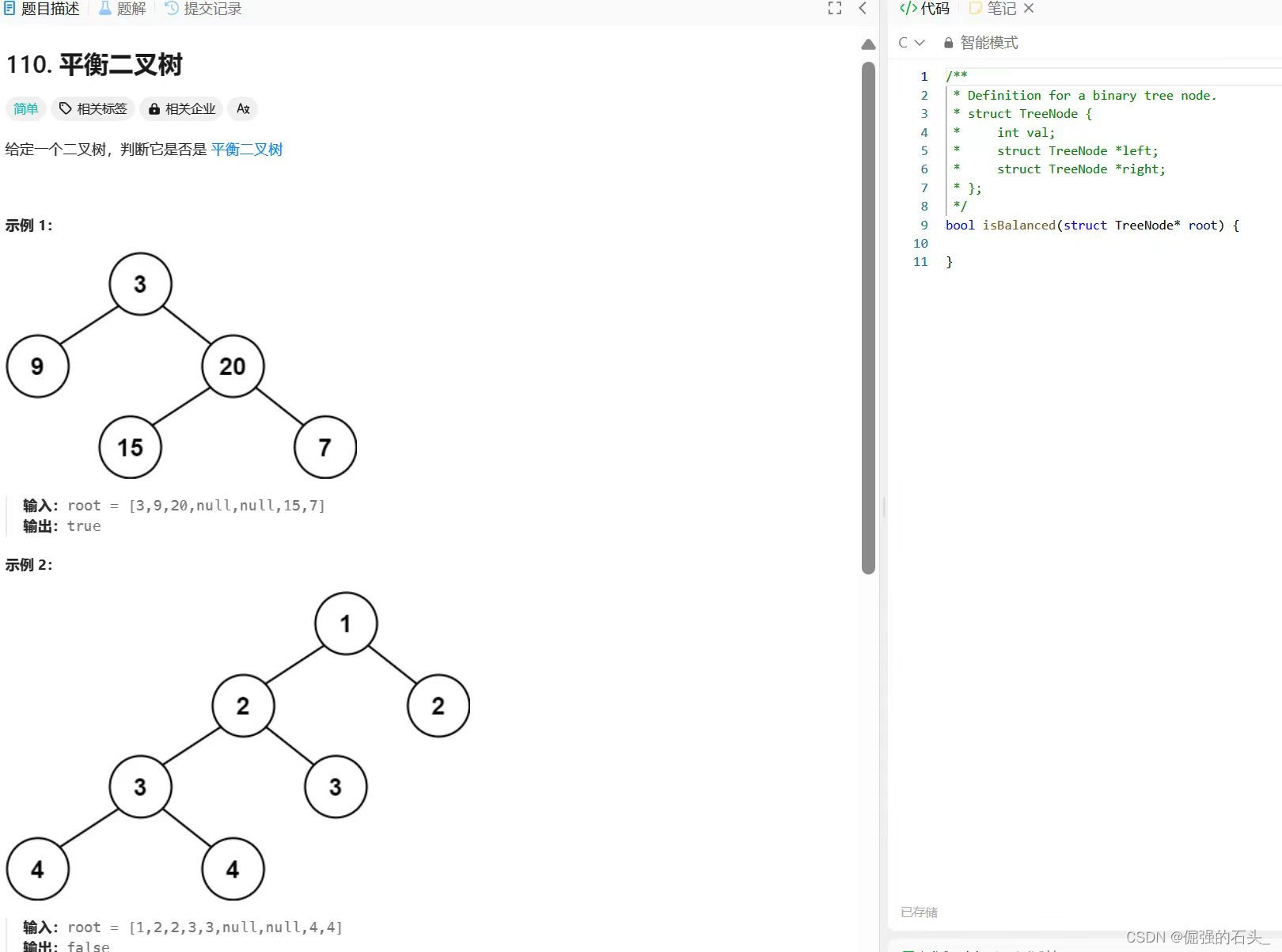
给定一个二叉树,判断它是否是平衡二叉树。平衡二叉树(Balanced Binary Tree)是一种特殊的二叉树,其中任一节点的左、右两个子树的高度差的绝对值不超过1,并且左、右两个子树都是一棵平衡二叉树。
·
💓 博客主页:倔强的石头的CSDN主页
📝Gitee主页:倔强的石头的gitee主页
⏩ 文章专栏:《数据结构与算法 经典例题》C语言
期待您的关注
目录
一、问题描述
给定一个二叉树,判断它是否是 平衡二叉树
平衡二叉树(Balanced Binary Tree)是一种特殊的二叉树,其中任一节点的左、右两个子树的高度差的绝对值不超过1,并且左、右两个子树都是一棵平衡二叉树。
原题出自
二、解题思路
解题思路:
判断平衡二叉树需要计算二叉树的高度,所以定义一个辅助函数,用于计算二叉树的高度。这个函数会递归地调用自身来计算左子树和右子树的高度,然后返回两者中的较大值加1(加上根节点的高度)。
更多细节可以参考下面这篇二叉树详解文章【数据结构与算法】详解二叉树下:实践篇————通过链式结构深入理解并实现二叉树-CSDN博客
- 在主函数中,使用递归的方式遍历二叉树的每一个节点。对于每个节点,先判断其是否为空树,或者左右子树为空,这两种情况都可以直接判定是平衡的。
- 之后判定其左子树和右子树是否都是平衡二叉树,然后计算左子树和右子树的高度差,如果高度差的绝对值大于1,则返回false,表示这棵树不是平衡二叉树。
- 递归调用左子树和右子树,如果都满足平衡二叉树的条件,则返回true。
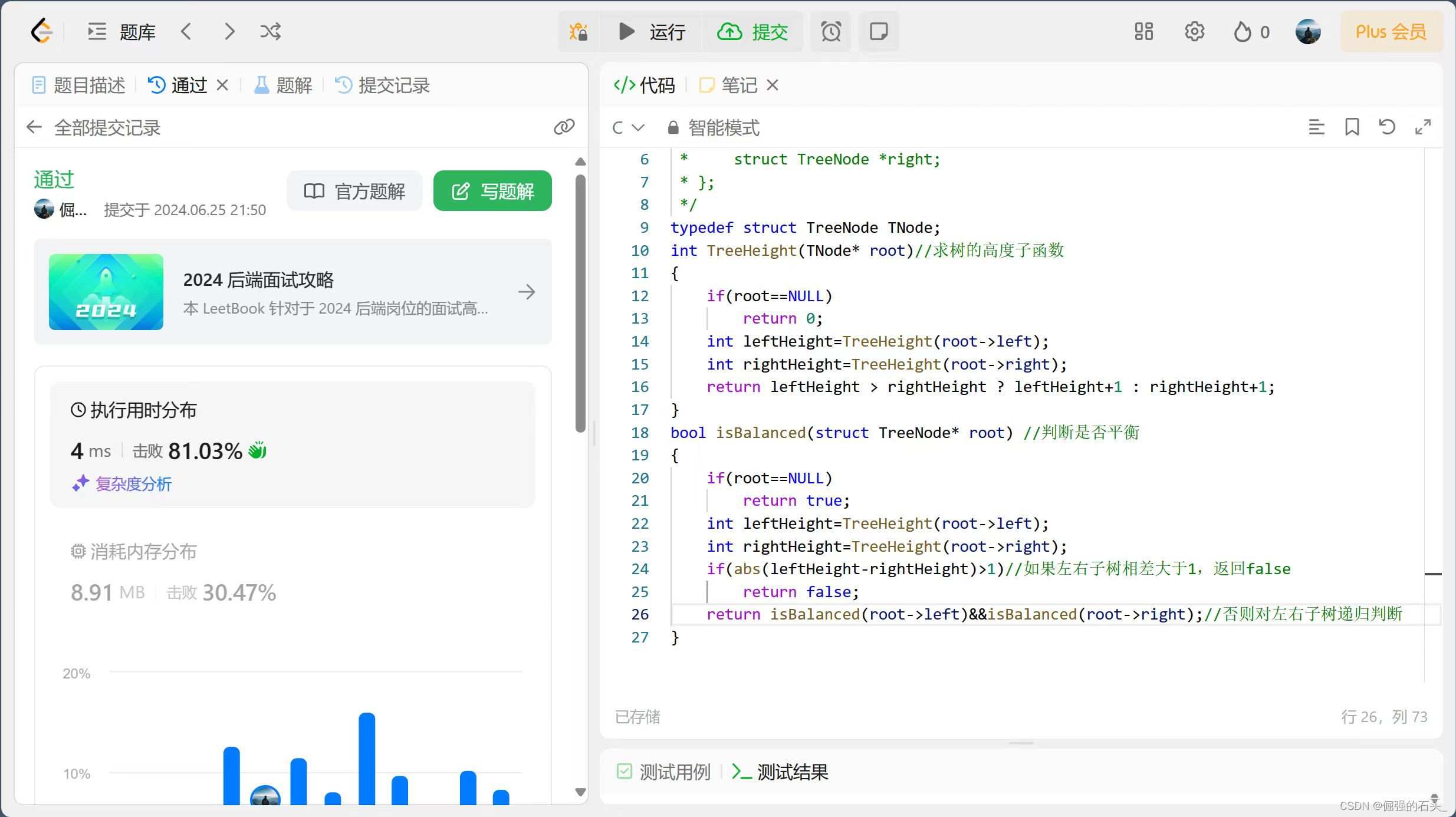
三、C语言实现代码
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
typedef struct TreeNode TNode;
int TreeHeight(TNode* root)//求树的高度子函数
{
if (root == NULL)
return 0;
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
bool isBalanced(struct TreeNode* root) //判断是否平衡
{
if (root == NULL)
return true;
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
if (abs(leftHeight - rightHeight) > 1)//如果左右子树相差大于1,返回false
return false;
return isBalanced(root->left) && isBalanced(root->right);//否则对左右子树递归判断
}

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容








所有评论(0)