弗洛伊德（Floyd）算法

算法思路：（学习过程中的个人理解，欢迎指导！）
首先是建图，同时定义两个二维数组，类似于迪杰斯特拉算法中的数组作用，二维数组D代表顶点到顶点的最短路径权值和的矩阵，二维数组P代表对应顶点的最小路径的前驱矩阵
如图，进行初始化后 分别命名为D^-1和P^-1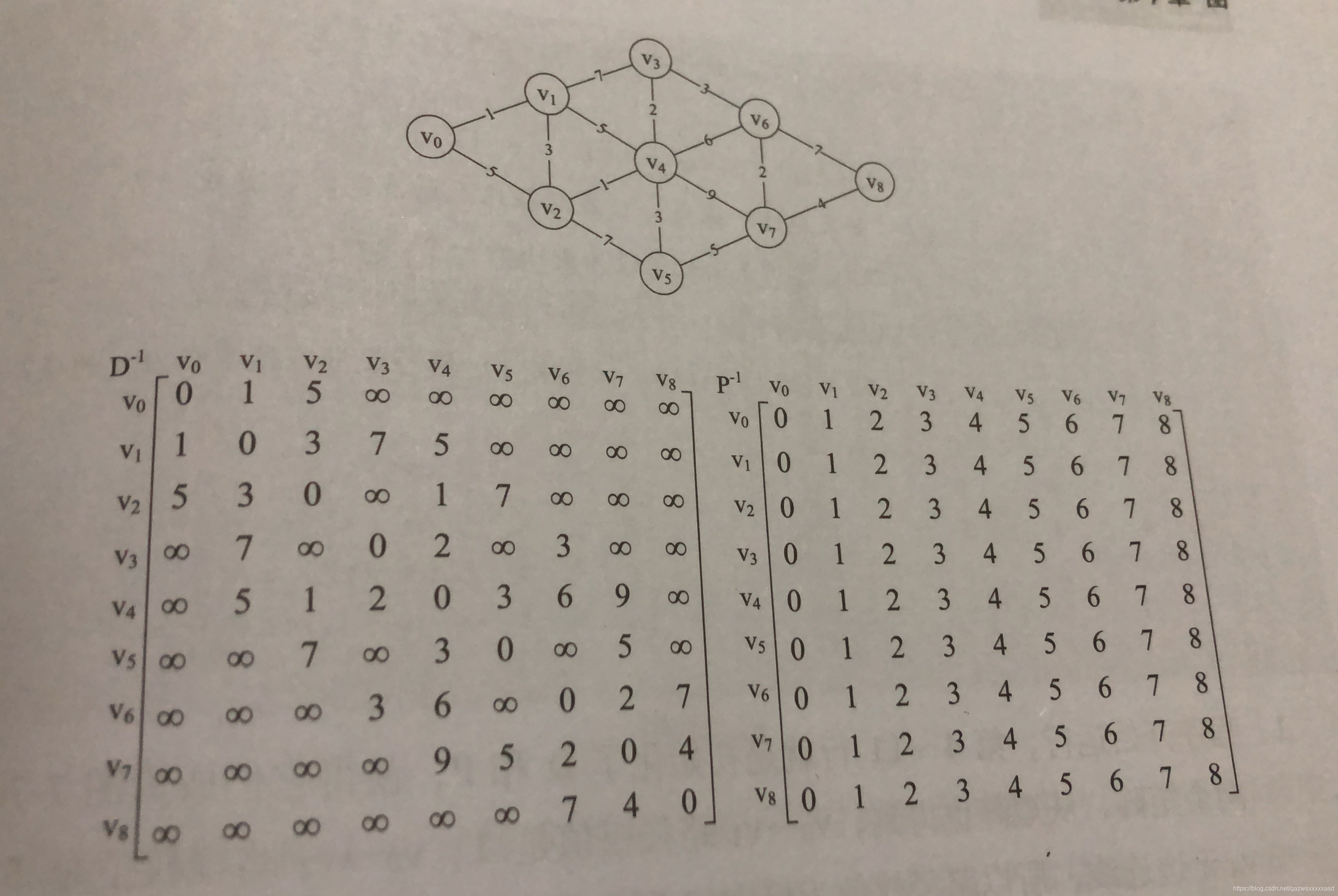

接下来是三层循环嵌套，v代表起始顶点，w代表结束顶点，k代表中转顶点的下标
K依次变化，k=0时，代表所有顶点都经过v0中转，此时无任何变化，当k=1时，都经过v1中转此时 D[0][2]=5<D[0][1]+D[1][2]=4,所以将D[0][2]修改为4，同时P[0][2]和P[2][0]修改为1，D[0][3],D[0][4]同理，一直到循环结束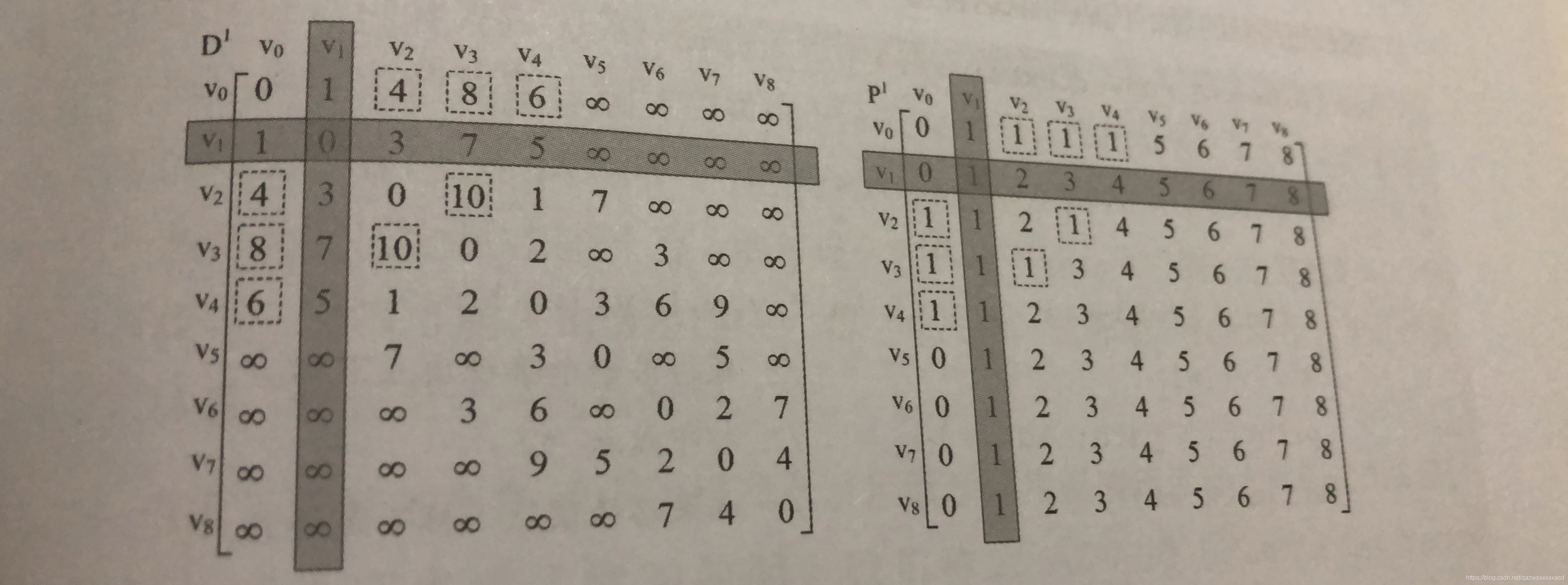

最终 D矩阵第v0行数值和迪杰斯特拉D数组最后的值也是一样的，而关于最短路径路线问题则要看P矩阵，比如从v0到v8,首先P【0】【8】=1，然后就看P【1】【8】=2，P【2】【8】=4由此一步步推，可得路线为v0->v1->v2->v4->v3->v6->v7->v8

#define MAXVEX 100 
typedef int Pathmatrix[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];

typedef char VertexType;
typedef int EdgeType;
typedef struct 
{
	VertexType vex[MAXVEX];
	EdgeType matrix[MAXVEX][MAXVEX];
	int numVertexes,numEdges;
}MGraph;

/*Floyd算法，求网图G中各顶点v到其余顶点w最短路径P[v][w]及带权长度D[v][w]*/

void ShortestPath_Floyd(MGraph G,Pathmatrix *P,ShortPathTable *D)
{
	int v,w,k;
	for(v=0;v<G.numVertexes;++v)//初始化D与P 
	{
		for(w=0;w<G.numVertexes;++w)
		{
			(*D)[v][w]=G.matrix[v][w];//D[v][w]的值即对应点间的权值 
			(*P)[v][w]=w;             //初始化P 
		}
	}
	for(k=0;k<G.numVertexes;++k)
	{
		for(v=0;v<G.numVertexes;++v)
		{
			for(w=0;w<G.numVertexes;++w)
			{
				if((*D)[v][w]>(*D)[v][k]+(*D)[k][w])
				{
					/*如果经过下标为k的顶点路径比原两点间路径更短*/
					/*将当前两点间权值设为更小的一个*/ 
					(*D)[v][w]=(*D)[v][k]+(*D)[k][w];
					(*P)[v][w]=(*P)[v][k];//路径设置经过下标为k的顶点 
				}
			}
		}
	}
	
}