C语言数据结构基础--队列

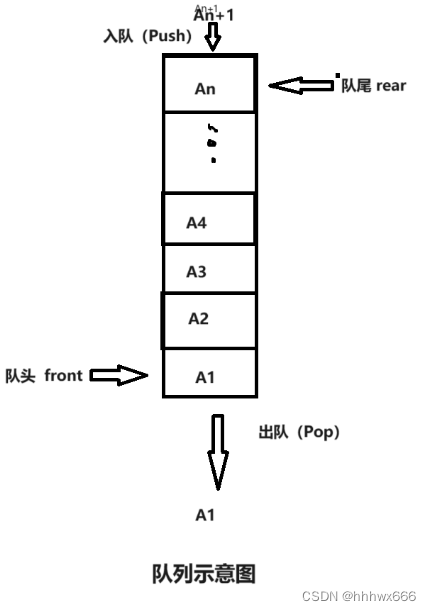
队列（Queue）是另一种限定性的线性表，它只允许在表的一端插入元素，在另一端删除元素，所以队列具有先进先出（First In First Out,FIFO)的特点。这个就与平日我们排队一样，先排的先离开，后来的排在队尾。而在队列中，排头也就是先离开(允许删除)的一端叫做队头(Front)，而队尾，也就是允许加入的一端叫做队尾(Rear)。

如果元素{A1，A2,A3...An}按照A1-->An的顺序入队，那么其出队顺序也是A1-->An;当然和栈一样，需要注意出入顺序。

队列在程序设计中也常常被使用。一个最典型的例子就是操作系统中的作业排队。在允许多道程序运行的计算机系统中，同时有几个作业在运行。如果运行的结果都要通过通道输出，那么就要讲究先来后到了，按照先进先出原则输出。

二.队列的实现

作为线性表的限制版本，自然与线性表一样，队列也有两种存储表示，顺序表示与链式表示。

01.链队列

用链表表示的队列简称为链队列。为了方便操作，这里也是采用了带头结点的链表结构，并且设置了一个队头指针front与队尾指针rear。

队头指针始终指向头结点，队尾指针指向最后一个元素。

空的链队列的头指针和尾指针均指向头结点。这也是判空条件。

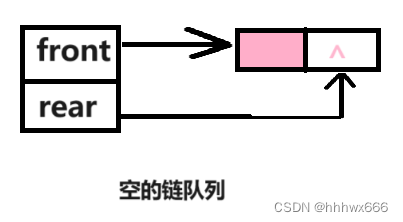
通常将front与rear封装在一个结构体中，并将该结构体类型重新命名为链队列类型。(当然，用数组封装也行，就像双端栈一样）

其数据结构定义代码如下：

// 队列 Queue 先进先出 FIFO
//链队列
typedef struct Link_Queue  
{ 
    int date;                 // 数据区
    struct Link_Queue* next; // next指针区
}LQ;

// 队列指针 封装在一起，当然可以用数组的方式，改改就行
typedef struct Queue_Ptr  
{
   LQ* front;  // 队头
   LQ* rear;  // 队尾

}ptq;

01-00-初始化

先在堆区开辟指针与节点空间。然后就是熟悉的置空操作，按照空链队列的定义来就行。

// 00-初始化
ptq* Init_LQ() {
    ptq* ptr = (ptq*)malloc(sizeof(ptq)); // 整个指针
    LQ* node = (LQ*)malloc(sizeof(LQ));   // 整个链表
    node->date = 0;                       // 初始化老几样
    node->next = NULL;                    // 头结点下一个元素，也就是第一个队列元素，尚未存在，指向空
    ptr->front = node;                    // 此时自然是头尾都没有
    ptr->rear = node;
    return ptr;
}

01-01-入队

链表表示，自然不必判断队列是否已满，后面的只是一个后插的操作，也就是将新的结点放在rear的后面，然后将rear指向新的结点。

// 01-入队
void Push_LQ(ptq* P) { // 从后进
    //不会满
    int x;
    printf("请输入所要压入的元素:\n");
    scanf("%d", &x);
    LQ* node = (LQ*)malloc(sizeof(LQ)); // 就是尾插法
    node->date = x;                     // 开辟新结点，接受新数据，前驱为rear，后继为rear->next
    node->next = P->rear->next;
    P->rear->next = node;
    P->rear = node;
    ++P->front->date;                   // 头结点存长度，因此++
}

01-02-出队

出的操作，无论是用什么结构表示都得判空，防止上溢。需要强调的就是队列先进先出，所以这里出的是队头元素，也就是头结点后面的元素。

// 02-出队
void Pop_LQ(ptq* P) { // 从先出
    //会空，且出队列后也会空，这时rear指针指向也要改变
    if (P->front != P->rear) { // 相同空，反之非空
        LQ* temp = P->front->next; // 记录第一个元素，日后好释放
        P->front->next = temp->next;
        if (temp == P->rear) { // 仅有一个元素，删除则为空
            P->rear = P->front; // 此时就要将rear又指向front，毕竟这是为空标志
        }
        free(temp);           // 释放
        --P->front->date;     // 元素数量--
    }
    else printf("空队列!!!\n");
}

01-03-遍历输出

遍历操作其实就和链表一样，不过结束标志可以通过NULL，也可以通过rear指针判断。

// 03-输出
void Out_LQ(ptq* P) {
    if (P->front != P->rear) {
        LQ* node = P->front->next; // 从第一队列元素开始
        while (node != NULL) { // 遍历完 因为最后一个元素后继无人，是空
            printf("%4d", node->date); 
            node = node->next; // 下一位
        }
        printf("\n");
    }
    else printf("空队列!!!\n");
}

02.循环队列

循环队列是队列中一种顺序表示和实现方法。与顺序栈类似，在队列的顺序存储结构中，用一组连续的存储空间依次存放从队头到队尾的元素。（为啥这开局就循环？用数组实现，如果要合理利用空间，就得在出队后，移动数组中元素，满足数组的队头始终在0的位置，在数组中很麻烦，因而将队头移动，整个队列看作环形循环，在此就要对队的指示器的移动进行巧劲，我想这是原因之一吧）

由于队列中队头与队尾的位置都是动态变化的，因此需要设置两个指针front与rear，分别指示队头元素与队尾元素在数组中的位置。

其数据结构定义代码如下：

const int Max = 10;
typedef struct Array_Queue
{
	int date[Max];
	int front;
	int rear;
}AQ;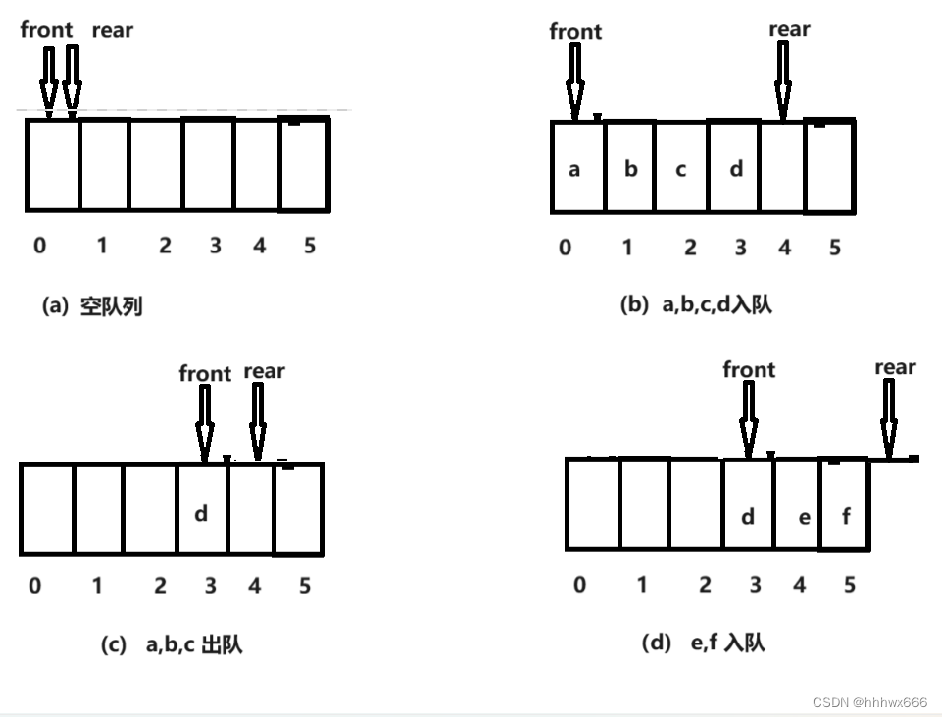

初始化队列时，令front=rear=0 ；入队时，直接将新元素送入尾指针rear所指的单元，然后尾指针增1；出队时，直接取出队头指针front所指的元素，然后头指针增加1。可以发现，rear其实并没有指向真正的队尾，而是指向了队尾后的单元。按照此思路，当rear==Max（设Max为数组最大长度）时，认为队列满。但很显然，只要发生过出队，前面就会有空余空间，此队列此刻并不满，而元素只从队尾入列，就会造成前面剩余单元浪费。此现象被称作假溢出。因此，如何才能准确的判断队列是否满？元素个数。毕竟是用数组表示，数组的刻板印--提前分配的固定的存储空间，所以队列中总元素个数一定，拿已入队的元素个数与最大元素个数进行判断。

然而，这只不过是解决了判断队列是否已满的问题，假溢出的问题如何解决？

传统思路上，既然出队会造成前面有空单元，那我每出队一个元素，我就把整个队列向前移动一个单元，那么假溢出问题迎刃而解，甚至都不用改变判断队列是否已满的条件。但我们都知道，每次挪动元素，时间复杂度都是O(n),如果队列元素多，出队又频繁，这就更费时了。

一个巧妙的办法是将顺序队列的数组看作一个环形的空间（注意，只是看作），即规定最后一个单元的后继为第一个单元，形象地称之为循环队列。假设队列数组为Queue[Max],当rear+1==Max时，令rear=0，就能求得最后一个单元Queue[Max]的后继：Queue[0]。通过数学中的取模（求余）操作，就可以自动实现队尾指针与队头指针的循环变化。进队时，尾指针rear=（rear+1）%Max；出队一样，队头指针front=（front+1）%Max；此时，队列情况如下：

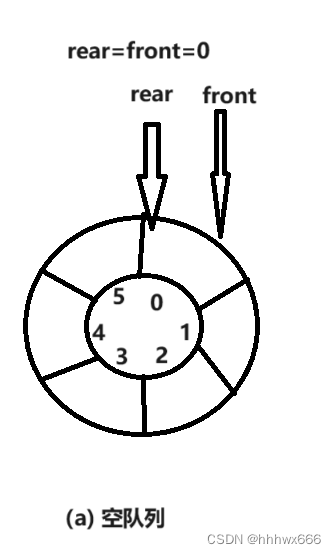
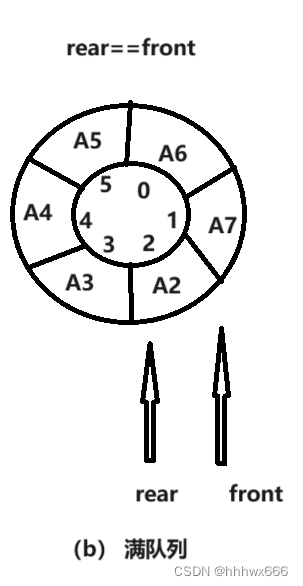
容易发现，空队列与满队列的rear都等于front，无法作为判断条件，当然，或许可以通过求元素个数来判断。结果会发现，求个数是不现实的，毕竟在空和满的情况下，求长度结果都是一样的。那就只能再设置变量记录个数了。

还有一种巧妙的方法，既然你空队列和满队列标志一样，那我特意留下最后一个单元不存放元素，当rear指针指向此元素，表示此队列已满，让rear不可能追上front。当然，这里的最后一个单元位置也是动态变化的，向后不好看，那就看作是front所指向单元的前一个单元，rear与front相邻，有人想，那不就是rear-front==1就行，表示相邻。（这里需要格外注意，因为这个数组的Queue[Max-1]后面元素下标为0，也就是开始新循环，此时，rear小于front，也就是rear与front的大小并不确定，用绝对值呢？你会发现，当队列只有一个元素时，|rear-front|==1，如何破局？）这里可以继续沿用前面模的思想，那就让rear前进一个和front重合即可，即为队列满，此时（rear+1）mod Max==front。（也可以把rear与front他们之间的距离用模表示，（front-rear+5）%5==1，当rear>front时，差为负，+5后取模恰好为之间的距离，为正，不影响）

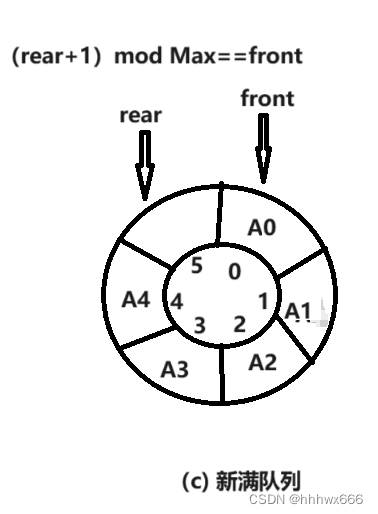
至此，就可以实现此循环队列了，本文采用损失一个单元格的方法来区别空队列与满队列。

02-01-初始化

开辟个元素区，然后指针赋值为0，表示空就行。

// 01-初始化顺序队列
AQ* Init_AQ() {
	AQ* L = (AQ*)malloc(sizeof(AQ)); // 在堆区开辟连续内存来存放数据元素
	L->front = 0;                    // 将front指针与rear指针都赋值为0，代表队列为空
	L->rear = 0;
	return L;
}

02-02-入队

重点就是判断队列是否已满，余下操作就是数组赋值。

// 02-入队
void Push_AQ(AQ* L) {  // 先进
	// 判断是否满
	// 标志? rear==front,这时我们发现，实际上在初始化时，rear==front ,也就是说，空队列也是如此，难以区别，故想对此进行区别，
	// 可以采用记录队内元素数量进行判定，也可以特地留下一个空元素，此时满队列标志就是rear与front相邻，
	// 如何判断相邻，自然不能单纯相减为1，因为是循环，最极端就是front==0，rear==Max-1,此时差值自然非1，
	// 这时模运算的重要性就体现了（front-rear+5）%5==1，当rear>front时，差为负，+5后取模恰好为之间的距离，为正，不影响
	// 后面的指针移动也依赖取模计算，才能满足循环
	if (((L->front - L->rear + Max) % Max) == 1) { // 满
		printf("队满!!!\t");
	}
	else {
		printf("请输入所要入队的元素:\n");
		int n;
		scanf("%d", &n);
		L->date[L->rear] = n;
		L->rear=(L->rear+1)%Max; // 此举为了循环
	}
}

02-03-出队

// 03-出队
void Pop_AQ(AQ* L) { // 先出
	// 队空? rear==front ,未必为0
	if (L->front == L->rear) {
		printf("队空!!!\t");
		return;
	}
	L->front = (L->front + 1) % Max; // 此举为了循环
}

02-04-遍历输出

那就是遍历数组，结束标志有些区别罢了。

// 04-输出
void Out_AQ(AQ* L) {
	if (L->front != L->rear) { // 非空 判空
		int it = L->front;
		printf("此队列如下:\n");
		while (it != L->rear) { // 从队头到队尾
			printf("%d  ", L->date[it]);
			it = (it + 1) % Max; // 循环数组特有的加一操作
		}
		printf("\n");
	}
	else printf("空队列!!!\n");
}

上述就是队列的两种基本样式以及其简单功能的实现。其应用会在下一篇文章。希望诸位可以帮我指正文中不当之处，共同进步。感谢！φ(゜▽゜*)♪

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。