实验内容

图的遍历

【题目描述】

利用邻接表或邻接矩阵存储图，并对图进行深度和广度优先遍历。

【步骤描述】

（1）定义图的邻接表或邻接矩阵存储；

（2）利用邻接表（或邻接矩阵）存储图；（参考图的邻接矩阵存储表示或图的邻接表存储表示）

（3）对图进行深度优先遍历；

（4）对图进行广度优先遍历；

（5）比较图的深度优先遍历和广度优先遍历两种遍历方法的不同及其时间和空间复杂度。

设计思想

图的邻接表存储

先定义图的邻接表存储结构，包括邻接表头节点名称和指向下一节点的指针，指针为空。从终端输入图的信息，几个节点，节点名称和几条边，有几个节点创建几个邻接表头节点并存入节点信息，再输入边的信息，起点和终点，按照输入边的信息节点指针依次指向终点，在邻接表上存储输入的信息，图的邻接表建立成功。

图的深度优先遍历

从图G的某个顶点v0出发，访问v0，然后选择一个与v0相邻且没被访问过的顶点vi访问，再从vi出发选择一个与vi相邻且未被访问的顶点vj进行访问，依次继续。如果当前被访问过的顶点的所有邻接顶点都已被访问，则退回到已被访问的顶点序列中最后一个拥有未被访问的相邻顶点的顶点w，从w出发按同样的方法向前遍历，直到图中所有顶点都被访问。

图的广度优先遍历

首先访问初始点vi，并将其标记为已访问过，接着访问vi的所有未被访问过的邻接点vi1,vi2,…, vi t，并均标记已访问过，然后再按照vi1,vi2,…, vi t的次序，访问每一个顶点的所有未被访问过的邻接点，并均标记为已访问过，依次类推，直到图中所有和初始点vi有路径相通的顶点都被访问过为止。

实验结果

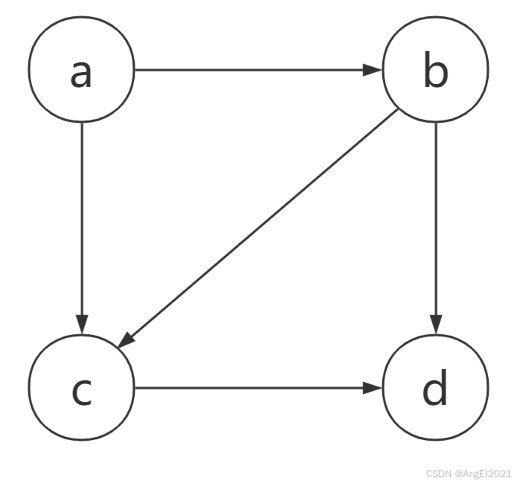
使用的有向图

运行结果

 

对（5）的回答

深度优先遍历使用的是栈，广度优先遍历使用的是队列；深度优先遍历对每一个可能的分支路径深入到不能再深入为止，每个节点只访问一次。广度优先遍历又叫层次遍历，从上往下对每一层进行访问，每一层中从左往右或从右往左访问节点，直到结束；深度优先遍历不保留全部节点，占用空间小，有回溯操作。广度优先遍历保留全部节点，占用空间大，无回溯操作。

深度优先遍历和广度优先遍历的时间复杂度为O（n），每个节点都会被访问一次且仅访问一次。

深度优先遍历的空间复杂度是O（d），无论实现（递归还是迭代），堆栈都将包含d个节点，其中d是最大深度。

广度优先遍历的空间复杂度是O（n），广度优先遍历在队列中至少存储整个图，n为节点的个数。

 源代码

#include<iostream>
#include<malloc.h>
using namespace std;
#define MAX 15
int visited[MAX]; //定义标志数组 
//定义主结点结构 
typedef struct Node {
	int adjvex; //邻接点域 
	struct Node* next; //指向下一邻接点的指针域 
}ALnode;
//定义顶点表结点 
typedef struct vexnode {
	char data; //顶点域 
	ALnode* firstal; //指向第一条边结点 
}HeadNode;
//定义图的邻接表存储结构 
typedef struct {
	HeadNode adjlist[MAX]; //邻接表头结点数组 
	int n; //图的当前顶点数 
	int e; //图的当前边数 
}Graph;
void CreateGraph(Graph& G)
{
	int i, j, k;
	ALnode* p;
	cout << "输入图的顶点数:";
	cin >> G.n;
	cout << "输入图的边数:";
	cin >> G.e;
	cout << endl;
	cout << "输入图的各顶点(存储序号从0开始)：" << endl;
	for (i = 0; i < G.n; i++) {  //生成有n个顶点的顶点表
		cout << "第" << i << "个顶点名称：";
		cin >> G.adjlist[i].data; //顶点数据存入表头 
		G.adjlist[i].firstal = NULL; //边表头指针域置为空 
	}
	cout << endl;
	cout << "输入图中的边，顶点序号从0开始:" << endl;
	for (k = 0; k < G.e; k++) {
		cout << endl;
		cout << "输入第" << k + 1 << "条边:" << endl;
		cout << "输入出发顶点的序号：";
		cin >> i;
		cout << "输入指向顶点的序号：";
		cin >> j;
		p = (ALnode*)malloc(sizeof(ALnode));
		p->adjvex = j;
		p->next = G.adjlist[i].firstal; //新结点的指针域置为空 
		G.adjlist[i].firstal = p; //新结点信息依次存入邻接表中 
	}
}
void PrintGraph(Graph G) {
	int i;
	ALnode* p;
	cout << "邻接表中的存储内容如下所示：" << endl;
	for (i = 0; i < G.n; i++) {
		cout << i << ' ' << G.adjlist[i].data; //输出表头结点的数据 
		p = G.adjlist[i].firstal; //指向下一结点 
		while (p != NULL) {
			cout << "--->" << p->adjvex << ' '; //输出结点信息 
			p = p->next;
		}
		cout << endl;
	}
}
//深度优先遍历
void DFS(Graph G, int v)
{
	ALnode* p;
	cout << "(" << v << "," << G.adjlist[v].data << ")" << ' '; //输出顶点信息 
	visited[v] = 1;
	p = G.adjlist[v].firstal; //访问第v个顶点
	while (p != NULL) {
		if (visited[p->adjvex] == 0)
			DFS(G, p->adjvex);
		p = p->next;
	}
}
//广度优先遍历
void BFS(Graph G, int v)
{
	int i, j, visited[MAX];
	ALnode* p;
	int queue[MAX], front = 0, rear = 0;
	for (i = 0; i < G.n; i++)
		visited[i] = 0; //标志数组信息初始化 
	cout << "(" << v << "," << G.adjlist[v].data << ")" << ' ';
	visited[v] = 1;
	rear = (rear + 1) % MAX;
	queue[rear] = v; //查找的顶点对应序号入队列 
	while (front != rear) {
		front = (front + 1) % MAX;
		j = queue[front]; //从队列中取出顶点对应序号 
		p = G.adjlist[j].firstal; //取对应序号的顶点信息 
		while (p != NULL) {
			if (visited[p->adjvex] == 0) {
				visited[p->adjvex] = 1;
				cout << "(" << p->adjvex << "," << G.adjlist[p->adjvex].data << ")" << ' ';
				rear = (rear + 1) % MAX;
				queue[rear] = p->adjvex; //查找的顶点对应序号入队列
			}
			p = p->next;
		}
	}
}
int main()
{
	Graph G;
	CreateGraph(G);
	PrintGraph(G);
	cout << "(序号从0开始)深度优先遍历结果为：" << endl;
	DFS(G, 0);
	cout << endl;
	for (int i = 0; i < G.n; i++)
		visited[i] = 0; //标志数组信息初始化
	cout << endl;
	cout << "(序号从0开始)广度优先遍历结果为：" << endl;
	BFS(G, 0);
	cout << endl;
	return 0;
}

 默认从0号节点开始遍历，可以定义一个变量实现自定义开始的节点

感谢大家的观看